poj 1556 题解

Posted 2020-09-22 心里只有学习

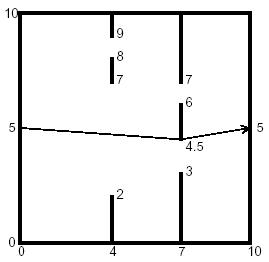题意：如图，大概猜的到了？最多18面墙，每面墙上两个门，从(0,5)走到(10,5)的最短距离，保留两位小数

题解:这道题非常贴心地按序给出墙的坐标，把每个端点当做图里面的一个节点，用O(n³)时间判断每两点之间是否能连边，判断方法为判断直线与线段是否相交(事实上是两个线段，但在这道题里面用直线交线段即可)，跑一个最短路即可(既然已经到了三次方级别，干脆写了最短的Floyd)

 

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;

#define rep(i,a,b) for (int i=a;i<=b;++i)

const double eps=1e-7;

struct point{
    double x,y;
    point(){}
    point (double a,double b): x(a),y(b) {}

    friend point operator + (const point &a,const point &b){
        return point(a.x+b.x,a.y+b.y);
    }

    friend point operator - (const point &a,const point &b){
        return point(a.x-b.x,a.y-b.y);
    }

    friend point operator * (const double &r,const point &a){
        return point(r*a.x,r*a.y);
    }

    friend bool operator == (const point &a,const point &b){
        return (abs(a.x-b.x)<eps && abs(a.y-b.y)<eps);
    }

    double norm(){
        return sqrt(x*x+y*y);
    }
};

inline double det(point a,point b) {return a.x*b.y-a.y*b.x;}
inline double dot(point a,point b) {return a.x*b.x+a.y*b.y;}
inline double dist(point a,point b) {return (a-b).norm();}

inline bool line_cross_segment(point s,point t,point a,point b)
{
    return !(det(s-a,t-a)*det(s-b,t-b)>eps);
}

int n,m;
point s[1000];
double dis[1000][1000],x,y;

bool ok(int a,int b)
{
    point ts=s[a],tt=s[b];
    if (a/4+(a%4!=0)==b/4+(b%4!=0)) return false;
    rep(i,a/4+(a%4!=0)+1,b/4+(b%4!=0)-1)
    {
        if (!line_cross_segment(ts,tt,s[(i-1)*4+1],s[(i-1)*4+2]) && !(line_cross_segment(ts,tt,s[(i-1)*4+3],s[(i-1)*4+4]))) return false;
    }
    return true;
}

int main()
{
    while (~scanf("%d",&n))
    {
        if (n==-1) break;
        m=4*n+1;
        rep(i,0,m)
            rep(j,0,m) dis[i][j]=1000000;
        rep(i,0,m) dis[i][i]=0;
        s[0]=point(0,5);
        rep(i,1,n)
        {
            scanf("%lf",&x);
            rep(j,1,4)
                {
                    scanf("%lf",&y);
                    s[4*(i-1)+j]=point(x,y);
                }

        }
        s[m]=point(10,5);
        rep(i,0,m)
            rep(j,i+1,m)
                if (ok(i,j)) dis[i][j]=dist(s[i],s[j]);
        rep(i,0,m)
            rep(j,0,m)
                rep(k,0,m)
                    dis[j][k]=min(dis[j][k],dis[j][i]+dis[i][k]);
        printf("%.2f\\n",dis[0][m]);
    }
}