插入排序

Posted 2020-06-23 欣麒骥

基本思想

每趟将一个待排序的对象，按其关键码大小，插入到前面已经排序好的一组对象的适当位置
上，直到对象全部插入为止。

即边插入边排序，保证子序列中随时都是排好序的

插入排序算法的分类

直接插入排序

折半插入排序

希尔排序

直接插入排序

排序过程：整个排序过程为n-1趟插入，即先将序列中第1个记录看成是一个有

序子序列，然后从第2个记录开始，逐个进行插入，直至整个序列有序。

void InsertSort（SqList &L）
{
int i，j；

  for(i=2;i<L.length;++i)

  if(L.r[i].key<L.r[i-1].key)        //"<",需将r[i]插入有序子表
  {            
  L.r[0]=L.r[i];      //将待插入的记录暂时存在监视岗哨中

  L.r[i]=L.r[i-1];     //r[i-1]后移

  for(j=i-2;L.r[0].key<L.r[j].key;--j)//从后向前寻找插入位置
  {

   L.r[j+1]=L.r[j];//记录逐个后移，直到找到插入位置

  }

  L.r[j+1]=L.r[0];    //将r[0]即原r[i]，插入到正确位置
  }
}

算法分析

设对象个数为n，则执行n-1趟

比较次数和移动次数与初始排序有关

最好情况下：

• 每趟只需要比较1次，不移动

• 总比较次数为n-1
  

最坏情况下：第i趟比较i次，移动i+1次

比较次数：KCN=（n+2）(n-1)/2=n*n/2

移动次数：RMN=(n+4)(n-1)/2=n*n/2

算法分析

• 若出现各种可能排序的概率相同，则可取最好情况和最坏情况的平均情况
  平均情况比较次数和移动次数为n*n/4

• 时间复杂度为O(n*n)

• 空间复杂度为O(1)

• 是一种稳定的排序方法

折半插入排序

折半插入排序建立在直接插入排序的基础上，是它的拓展出来的东西.

我们在将一个新元素插入已经排好序的数组的过程中，寻找插入点时，将待插入

区域的上限设置为a[low],下限设置为a【high】,然后将待插入元素与区间中间

位置a[m]进行比较，其中m=（low+high）/2

如果比中间位置a[m]小，则选择a[low]到a[m-1]为新的插入区域(即high=m-1)，

如果比中间位置a[m]大，则选择a[m+1]到a[high]为新的插入区域(即low=m+1)

(3)如此直至low<=high不成立，即将此位置之后所有元素后移一位，并将新元素插入a[high+1]

Void BInserSort(SqList &L)
{
  for(i=2;i<L.Length;++i)//对顺序表L做折半插入排序
  {
   L.r[0]=L.r[i];//将待插入的记录暂存到监视哨中
   low=1;high=i-1;//置查找区间初值
   while(low<=high)  //在r[low.high]中折半查找插入的位置
   {
m=(low+high)/2   //折半
if(L.r[0].key<L.r[m].Key) high=m-1;//插入点在前一个子表
else low=m+1;      //插入点在后一子表
   }
   for(j=i-1;j>high+1;--j) L.r[j+1]=L.r[j];//记录后移
   L.r[high+1]=L.r[0];   //将r[0]即原r【i】，插入到正确位置
  }

}

算法分析

折半查找比顺序查找快，所以折半插入排序就平均性能来说比直接插入排序要快

它所需要的关键码比较次数与待排序对象序列的初始化排列无关，仅依赖于对象个数。在插入第i个对象时，需要经过log2i+1次关键码比较，才能确定它应插入的位置

当n较大时，总关键码比较次数比直接插入排序的最坏情况要好得多，但其最好的情况要差

在对象的初始排列已经按关键码排好序或接近有序时，直接插入排序比折半

插入排序执行的关键码比较次数要少

折半插入排序的对象移动次数与直接插入排序相同，依赖于对象的初始排列

• 减少了比较次数，但没有减少移动次数

• 平均性能优于直接插入排序

• 时间复杂度为O(n*n)

• 空间复杂度为O(1)

• 是一种稳定的排序方法

• 只能用于顺序结构，不能用于链式结构

• 适合初始记录无序，n较大的情况

希尔排序

希尔排序是1959年由D.L.Shell提出来的，相对直接插入排序有较大的改进。希尔排序又叫缩小增量排序。

算法思想的出发点：

直接插入排序在基本有序时，效率较高

在待排序的记录个数较少时，效率较高

基本思想：

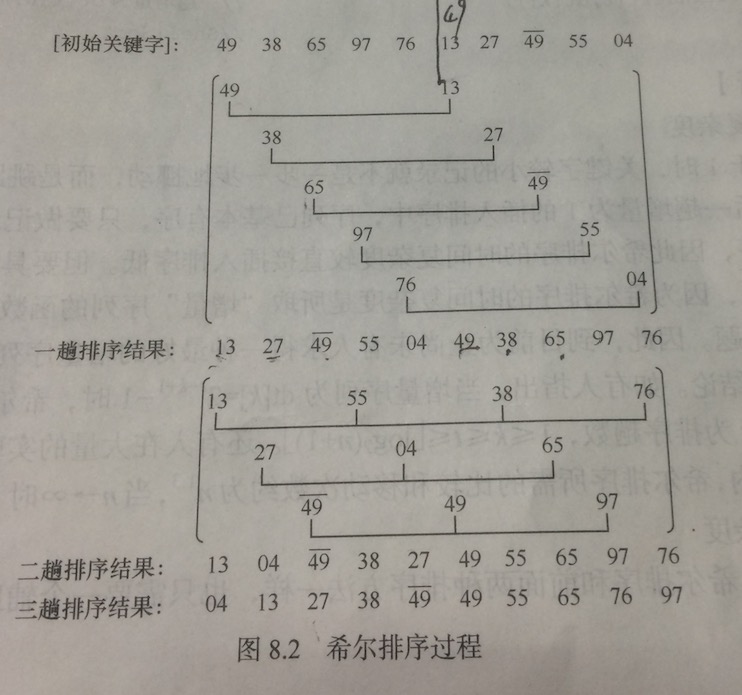
先将整个待排记录序列按某个增量d分割成若干组子序列，每组中记录的下标

相差d，分别对每组进行直接插入排序，然后再用一个较小的增量对它进行分

组，在每组中再进行直接插入排序。这样当经过几次分组排序后，待整个序

列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

技巧：

子序列的构成不是简单地“逐段分割”将相隔某个增量dk的记录组成一组子序

列让增量dk逐趟缩短（例如依次取5，3，1）

直到dk=1为止。

优点：

• 小元素跳跃式前移

• 最后一趟增量为1时，序列已基本有序

• 平均性能优于直接插入排序

  void ShellInsert(SqList &L,int dk)
  {
   for(i=dk+1;i<=L.length;++i)
  
   if(L.r[i].Key<L.r[i-dk].key)
   {
    L.r[0]=L.r[i];
    for(j=i-dk;j>0&&L.r[0].key<L.r[j].key;j-=dk)
    {
      L.r[j+dk]=L.r[j];
  
    }
       L.r[j+dk]=L.r[0];
    }
  
  }
  
  void ShellSort(SqList &L,int dt[],int t)
  {
   for(k=0;k<t;++k)
   {
  
        ShellInsert(L,dt[k]);
       }
  }