降维之pca算法
Posted Gxjun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了降维之pca算法相关的知识,希望对你有一定的参考价值。
pca算法:
算法原理: pca利用的两个维度之间的关系和协方差成正比,协方差为0时,表示这两个维度无关,如果协方差越大这表明两个维度之间相关性越大,因而降维的时候,
都是找协方差最大的。
1 将XX中的数据进行零均值化,即每一列都减去其均值。 2 计算协方差矩阵C=1mXTXC=1mXTX 3 求出CC的特征值和特征向量 4 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P 5 Y=XPY=XP就是降维到k维后的数据。
代码:
# coding=utf-8 import matplotlib.pyplot as plt from sklearn.decomposition import PCA from sklearn.datasets import load_iris data = load_iris() y = data.target X = data.data print data.feature_names print data.data; pca = PCA(n_components=2) reduced_X = pca.fit_transform(X) red_x, red_y = [], [] blue_x, blue_y = [], [] green_x, green_y = [], [] for i in range(len(reduced_X)): if y[i] == 0: red_x.append(reduced_X[i][0]) red_y.append(reduced_X[i][1]) elif y[i] == 1: blue_x.append(reduced_X[i][0]) blue_y.append(reduced_X[i][1]) else: green_x.append(reduced_X[i][0]) green_y.append(reduced_X[i][1]) plt.scatter(red_x, red_y, c=\'r\', marker=\'x\') plt.scatter(blue_x, blue_y, c=\'b\', marker=\'D\') plt.scatter(green_x, green_y, c=\'g\', marker=\'.\') plt.show()
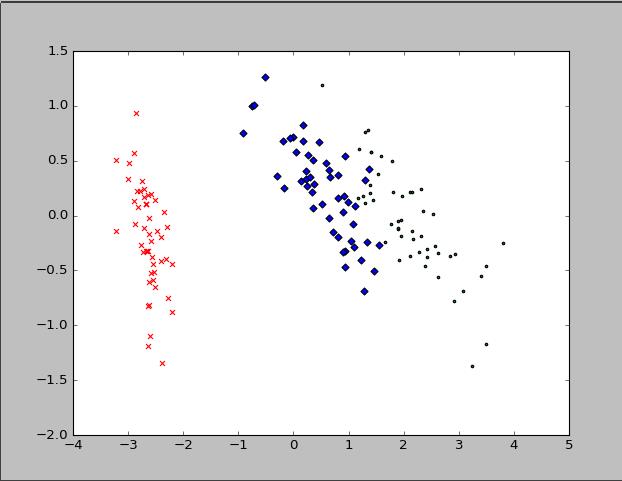
以上是关于降维之pca算法的主要内容,如果未能解决你的问题,请参考以下文章