『cs231n』限制性分类器损失函数和最优化
Posted 叠加态的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了『cs231n』限制性分类器损失函数和最优化相关的知识,希望对你有一定的参考价值。
代码部分
SVM损失函数 & SoftMax损失函数:
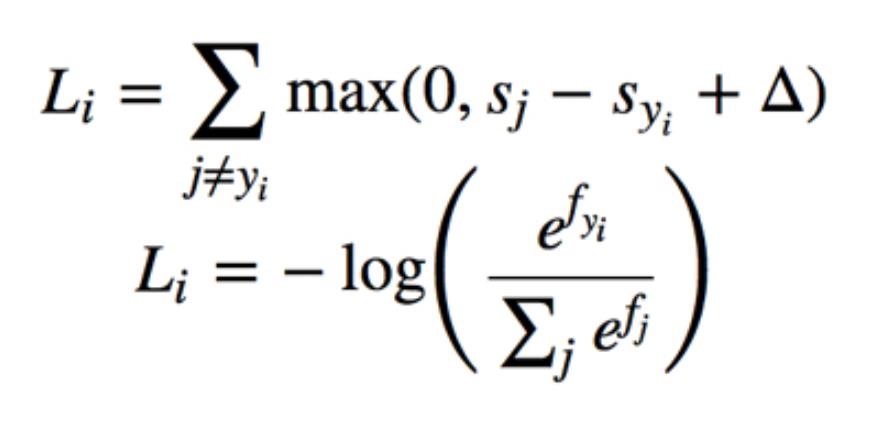
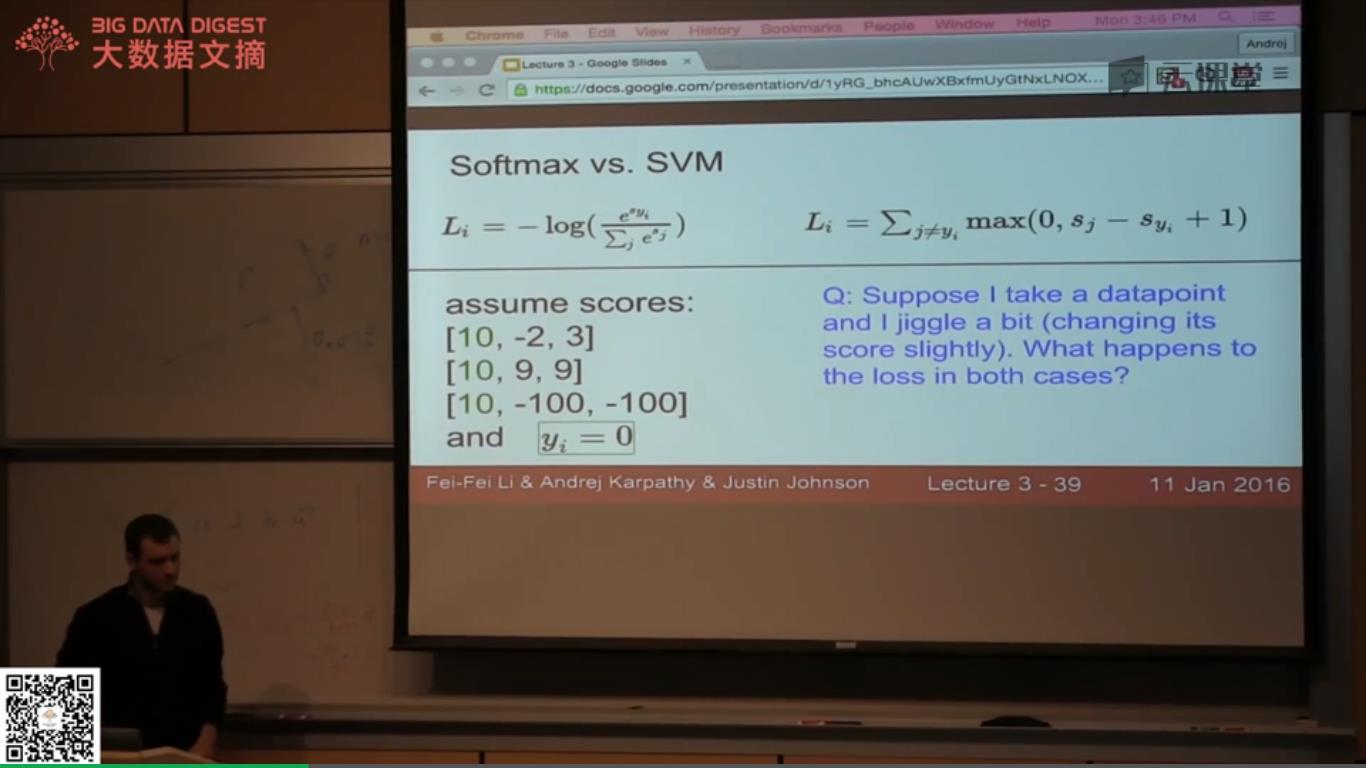
注意一下softmax损失的用法:

SVM损失函数:
import numpy as np
def L_i(x, y, W):
\'\'\'
非向量化SVM损失计算
:param x: 输入矢量
:param y: 标准分类
:param W: 参数矩阵
:return:
\'\'\'
delta = 1.0
scores = W.dot(x)
correct_score = scores[y]
D = W.shap[0]
loss_i = 0.0
for j in range(D):
if j==y:
continue
loss_i += max(0.0, scores[j] - correct_score + delta)
return loss_i
def L_i_vectorized(x, y, W):
\'\'\'
半向量化SVM损失计算
:param x: 输入矢量
:param y: 标准分类
:param W: 参数矩阵
:return:
\'\'\'
delta = 1.0
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + delta)
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
softmax分类器:
import numpy as np # 正常的softmax分类器 f = np.array([123, 456, 789]) # p = np.exp(f) / np.sum(np.exp(f)) # print(p) # 数值稳定化的softmax分类器 f -= np.max(f) p = np.exp(f) / np.sum(np.exp(f)) print(p)
SoftMax实际应用
练习,softmax 模型:
Note: 你的 softmax(x) 函数应该返回一个形状和x相同的NumPy array类型。
例如,当输入为一个列表或者一维矩阵(用列向量表示一个样本样本)时,比如说以下的:
scores = [1.0, 2.0, 3.0]
应该返回一个同样长度(即3个元素)的一维矩阵:
print softmax(scores)
[ 0.09003057 0.24472847 0.66524096]
对于一个二维矩阵,如以下(列向量表示单个样本),例如:
scores = np.array([[1, 2, 3, 6],
[2, 4, 5, 6],
[3, 8, 7, 6]])
该函数应该返回一个同样大小(3,4)的二维矩阵,如以下:
[[ 0.09003057 0.00242826 0.01587624 0.33333333]
[ 0.24472847 0.01794253 0.11731043 0.33333333]
[ 0.66524096 0.97962921 0.86681333 0.33333333]]
每个样本(列向量)中的概率加起来应当等于 1。你可以用以上的例子来测试你的函数。
ANSWER:
"""Softmax."""
scores = [3.0, 1.0, 0.2]
import numpy as np
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
return np.exp(x)/np.sum(np.exp(x),axis=0)
print(softmax(scores))
# Plot softmax curves
import matplotlib.pyplot as plt
x = np.arange(-2.0, 6.0, 0.1)
scores = np.vstack([x, np.ones_like(x), 0.2 * np.ones_like(x)])
plt.plot(x, softmax(scores).T, linewidth=2)
plt.show()
比较好玩的是plt.plot(x, softmax(scores).T)中,后面的转置了,多线画图时,后面的都是要转置的,因为plt必须要求x和y第一维度大小相等:
plt.plot(np.linspace(0,1,100),np.asarray([10*np.linspace(0,2,100),10*np.linspace(0,1,100)]).T,linewidth=2) # 可以绘图 # 查看一下shape: np.linspace(0,1,100).shape # Out[26]: # (100,) np.asarray([10*np.linspace(0,2,100),10*np.linspace(0,1,100)]).shape # Out[25]: # (2, 100) # 必须对应x,y的第一维度大小
SoftMax特点
SoftMax(y*10)后分类器会更自信,SoftMax(y/10)后分类器会失去自信(结果概率平均化)
概念部分
 损失函数=代价函数=目标函数
损失函数=代价函数=目标函数




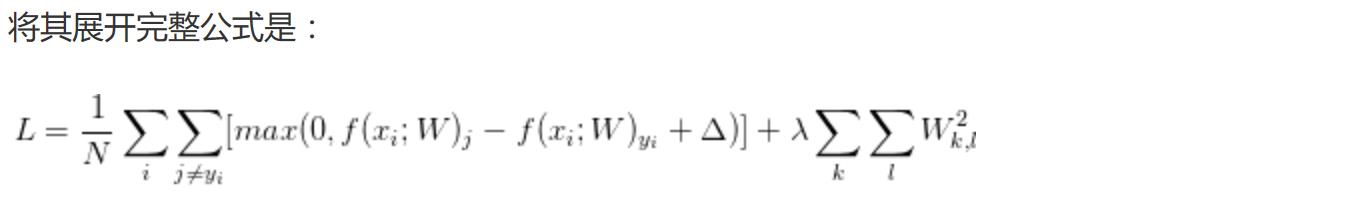


svm给出一个得分,softmax给出一个概率。
以上是关于『cs231n』限制性分类器损失函数和最优化的主要内容,如果未能解决你的问题,请参考以下文章
