POJ 题目1145/UVA题目112 Tree Summing(二叉树遍历)
Posted jzssuanfa
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POJ 题目1145/UVA题目112 Tree Summing(二叉树遍历)相关的知识,希望对你有一定的参考价值。
Tree Summing
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 8132 | Accepted: 1949 |
Description
LISP was one of the earliest high-level programming languages and, with FORTRAN, is one of the oldest languages currently being used. Lists, which are the fundamental data structures in LISP, can easily be adapted to represent
other important data structures such as trees.
This problem deals with determining whether binary trees represented as LISP S-expressions possess a certain property.
Given a binary tree of integers, you are to write a program that determines whether there exists a root-to-leaf path whose nodes sum to a specified integer. For example, in the tree shown below there are exactly four root-to-leaf paths. The sums of the paths are 27, 22, 26, and 18.
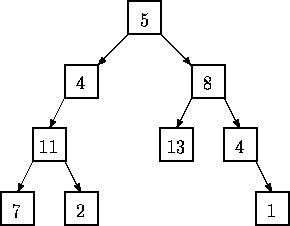
Binary trees are represented in the input file as LISP S-expressions having the following form.
The tree diagrammed above is represented by the expression (5 (4 (11 (7 () ()) (2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )
Note that with this formulation all leaves of a tree are of the form (integer () () )
Since an empty tree has no root-to-leaf paths, any query as to whether a path exists whose sum is a specified integer in an empty tree must be answered negatively.
This problem deals with determining whether binary trees represented as LISP S-expressions possess a certain property.
Given a binary tree of integers, you are to write a program that determines whether there exists a root-to-leaf path whose nodes sum to a specified integer. For example, in the tree shown below there are exactly four root-to-leaf paths. The sums of the paths are 27, 22, 26, and 18.

Binary trees are represented in the input file as LISP S-expressions having the following form.
empty tree ::= () tree ::= empty tree (integer tree tree)
The tree diagrammed above is represented by the expression (5 (4 (11 (7 () ()) (2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )
Note that with this formulation all leaves of a tree are of the form (integer () () )
Since an empty tree has no root-to-leaf paths, any query as to whether a path exists whose sum is a specified integer in an empty tree must be answered negatively.
Input
The input consists of a sequence of test cases in the form of integer/tree pairs. Each test case consists of an integer followed by one or more spaces followed by a binary tree formatted as an S-expression as described above. All
binary tree S-expressions will be valid, but expressions may be spread over several lines and may contain spaces. There will be one or more test cases in an input file, and input is terminated by end-of-file.
Output
There should be one line of output for each test case (integer/tree pair) in the input file. For each pair I,T (I represents the integer, T represents the tree) the output is the string yes if there is a root-to-leaf path in T
whose sum is I and no if there is no path in T whose sum is I.
Sample Input
22 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
20 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
10 (3
(2 (4 () () )
(8 () () ) )
(1 (6 () () )
(4 () () ) ) )
5 ()
Sample Output
yes no yes no
Source
题目大意:给出一个二叉树的表达式,问有没有一个路径和是n
ac代码
Problem: 1145 User: kxh1995 Memory: 164K Time: 0MS Language: C++ Result: Accepted
#include<stdio.h>
int tree_sum(int n)
{
int ans=0,m;
if(scanf(" (%d",&m))
{
ans=tree_sum(n-m)+tree_sum(n-m);
if(ans<2)
ans=0;
}
else
ans=!n;
scanf(" )");
return ans;
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
if(tree_sum(n))
printf("yes\n");
else
printf("no\n");
}
}以上是关于POJ 题目1145/UVA题目112 Tree Summing(二叉树遍历)的主要内容,如果未能解决你的问题,请参考以下文章