机器学习-牛顿方法&指数分布族&GLM

Posted 2020-09-21

本节内容

• 牛顿方法
• 指数分布族
• 广义线性模型

之前学习了梯度下降方法，关于梯度下降（gradient descent），这里简单的回顾下【参考感知机学习部分提到的梯度下降(gradient descent)】。在最小化损失函数时，采用的就是梯度下降的方法逐步逼近最优解，规则为其实梯度下降属于一种优化方法，但梯度下降找到的是局部最优解。如下图：

本节首先讲解的是牛顿方法（NewTon’s Method）。牛顿方法也是一种优化方法，它考虑的是全局最优。接着还会讲到指数分布族和广义线性模型。下面来详细介绍。

1.牛顿方法

现在介绍另一种最小化损失函数?(θ)的方法——牛顿方法,参考Approximations Of Roots Of Functions – Newton’s Method
。它与梯度下降不同，其基本思想如下：

假设一个函数我们需要求解此时的x值。如下图所示：

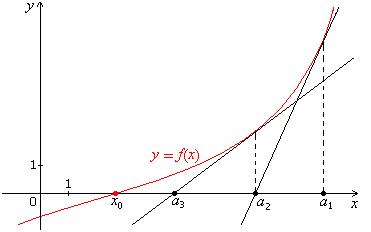
图1 f(x0)=0,a1,a2,a3...逐步接近x0

在a1点的时候，f(x)切线的目标函数由于(a2,0)在这条线上，所以我们有

同理，在a2点的时候，切线的目标函数由于(a3,0)在这条线上，所以我们有

假设在第n次迭代，有那么此时有下面这个递推公式：

其中n>=2。

最后得到的公式也就是牛顿方法的学习规则，为了和梯度下降对比，我们来替换一下变量，公式如下：

那么问题来了，怎么将牛顿方法应用到我们的问题上，最小化损失函数l(theta),(或者是求极大似然估计的极大值)呢？

对于机器学习问题，现在我们优化的目标函数为极大似然估计l,当极大似然估计函数取值最大时，其导数为 0，这样就和上面函数f取 0 的问题一致了，令极大似然函数的求解更新规则是：

对于l,当一阶导数为零时，有极值；此时，如果二阶导数大于零，则l有极小值，如果二阶导数小于零，则有极大值。

上面的式子是当参数θ为实数时的情况，下面我们要求出一般式。当参数为向量时，更新规则变为如下公式：

其中和之前梯度下降中提到的一样，是梯度，H是一个n*n矩阵，H是函数的二次导数矩阵，被成为Hessian矩阵。其某个元素H_ij计算公式如下：

和梯度下降相比，牛顿方法的收敛速度更快，通常只要十几次或者更少就可以收敛，牛顿方法也被称为二次收敛（quadratic convergence），因为当迭代到距离收敛值比较近的时候，每次迭代都能使误差变为原来的平方。缺点是当参数向量较大的时候，每次迭代都需要计算一次 Hessian 矩阵的逆，比较耗时。