注意力机制与外部记忆
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了注意力机制与外部记忆相关的知识,希望对你有一定的参考价值。
参考技术A根据通用近似定理,前馈网络和循环网络都有很强的能力。但由于优化算法和计算能力的限制,在实践中很难达到通用近似的能力。
神经网络中可以存储的信息量称为 网络容量(Network Capacity) 。一般来讲,利用一组神经元来存储信息时,其 存储容量和神经元的数量以及网络的复杂度成正比 。如果要存储越多的信息,神经元数量就要越多或者网络要越复杂,进而导致神经网络的参数成倍地增加。
大脑神经系统有两个重要机制可以解决信息过载问题: 注意力和记忆机制 。我们可以借鉴人脑解决信息过载的机制,从两方面来提高神经网络处理信息的能力。 一方面是注意力,通过自上而下的信息选择机制来过滤掉大量的无关信息;另一方面是引入额外的外部记忆,优化神经网络的记忆结构来提高神经网络存储信息的容量 。
在计算能力有限情况下,注意力机制(Attention Mechanism)作为一种资源分配方案,将计算资源分配给更重要的任务,是解决信息超载问题的主要手段。
注意力是一种人类不可或缺的复杂认知功能,指人可以在关注一些信息的同时忽略另一些信息的选择能力 。
注意力一般分为两种:一种是自上而下的有意识的注意力,称为 聚焦式(Focus)注意力 。聚焦式注意力是指有预定目的、依赖任务的、主动地有意识地聚焦于某一对象的注意力;另一种是自下而上的无意识的注意力,称为 基于显著性(Saliency-Based)的注意力 。基于显著性的注意力是由外界刺激驱动的注意,不需要主动干预,也和任务无关。
一个和注意力有关的例子是 鸡尾酒会效应 。当一个人在吵闹的鸡尾酒会上和朋友聊天时,尽管周围噪音干扰很多,他还是可以听到朋友的谈话内容,而忽略其他人的声音(聚焦式注意力)。同时,如果未注意到的背景声中有重要的词(比如他的名字),他会马上注意到(显著性注意力)。
在目前的神经网络中,我们 可以将最大汇聚(Max Pooling)、门控(Gating)机制来近似地看作是自下而上的基于显著性的注意力机制 。除此之外,自上而下的会聚式注意力也是一种有效的信息选择方式。
用 表示 组输入信息,其中每个向量 都表示一组输入信息。为了节省计算资源,不需要将所有信息都输入到神经网络,只需要从 中选择一些和任务相关的信息。 注意力机制的计算可以分为两步:一是在所有输入信息上计算注意力分布,二是根据注意力分布来计算输入信息的加权平均 。
给定一个和任务相关的查询向量 ,我们用注意力变量 来表示被选择信息的索引位置,即 表示选择了第 个输入向量。为了方便计算,我们采用一种“软性”的信息选择机制,首先计算在给定 和 下,选择第 个输入向量的概率 :
其中 称为注意力分布(Attention Distribution), 为 注意力打分函数 ,可以使用以下几种方式来计算:
其中 为可学习的网络参数, 为输入向量的维度。理论上,加性模型和点积模型的复杂度差不多,但是点积模型在实现上可以更好地利用矩阵乘积,从而计算效率更高。但当输入向量的维度 比较高,点积模型的值通常有比较大方差,从而导致 函数的梯度会比较小。因此,缩放点积模型可以较好地解决这个问题。
上式称为 软性注意力机制(Soft Attention Mechanism) 。下图给出了软性注意力机制的示例。
上面提到的注意力是 软性注意力,其选择的信息是所有输入向量在注意力分布下的期望。此外,还有一种注意力是只关注到某一个输入向量,叫做硬性注意力 。
硬性注意力有两种实现方式:
其中 为概率最大的输入向量的下标,即
硬性注意力的一个缺点是基于最大采样或随机采样的方式来选择信息。因此最终的损失函数与注意力分布间的函数关系不可导,因此无法用反向传播算法进行训练(硬性注意力需要通过强化学习来进行训练) 。为了使用反向传播算法,一般使用软性注意力来代替硬性注意力。
更一般地,我们可以用 键值对(key-value pair) 格式来表示输入信息,其中“键”用来计算注意力分布 ,“值”用来计算聚合信息。
用 表示 组输入信息,给定任务相关的查询向量 时,注意力函数为:
下图给出键值对注意力机制的示例。当 时,键值对模式就等价于普通的注意力机制。
多头注意力(Multi-Head Attention)是利用多个查询 ,来平行地计算从输入信息中选取多组信息。每个注意力关注输入信息的不同部分 。
其中 表示向量拼接。
在之前介绍中,我们假设所有的输入信息是同等重要的,是一种扁平(Flat)结构,注意力分布实际上是在所有输入信息上的多项分布。但 如果输入信息本身具有层次结构,比如文本可以分为词、句子、段落、篇章等不同粒度的层次,我们可以使用层次化的注意力来进行更好的信息选择 。
注意力机制一般可以用作一个神经网络中的组件。
注意力机制可以分为两步:一是计算注意力分布 ,二是根据 来计算输入信息的加权平均。我们可以只利用注意力机制中的第一步,并 将注意力分布作为一个软性的指针(pointer)来指出相关信息的位置 。
指针网络(Pointer Network) 是一种序列到序列模型, 输入是长度为 的向量序列 , 输出是下标序列 。
和一般的序列到序列任务不同,这里的输出序列是输入序列的下标(索引) 。比如输入一组乱序的数字,输出为按大小排序的输入数字序列的下标。比如输入为20, 5, 10,输出为1, 3, 2。
条件概率 可以写为:
其中条件概率 可以通过注意力分布来计算。假设用一个循环神经网络对 进行编码得到向量 ,则:
其中 为在解码过程的第 步时,每个输入向量的未归一化的注意力分布:
其中 为可学习的参数。下图给出指针网络的示例。
当使用神经网络来处理一个变长的向量序列时,我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列。
基于卷积或循环网络的序列编码都是可以看做是一种局部的编码方式,只建模了输入信息的局部依赖关系。虽然循环网络理论上可以建立长距离依赖关系,但是由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系 。如果要建立输入序列之间的长距离依赖关系,可以使用以下两种方法:一种方法是 增加网络的层数 ,通过一个深层网络来获取远距离的信息交互;另一种方法是 使用全连接网络 。全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列。不同的输入长度,其连接权重的大小也是不同的。这时我们就可以 利用注意力机制来“动态”地生成不同连接的权重,这就是自注意力模型(Self-Attention Model) 。
假设输入序列为 ,输出序列为 ,首先我们可以通过线性变换得到三组向量序列:
其中 分别为查询向量序列,键向量序列和值向量序列, 分别为可学习的参数矩阵。
利用键值对的注意力函数,可以得到输出向量 :
其中 为输出和输入向量序列的位置, 连接权重 由注意力机制动态生成 。
下图给出全连接模型和自注意力模型的对比,其中实线表示为可学习的权重,虚线表示动态生成的权重。 由于自注意力模型的权重是动态生成的,因此可以处理变长的信息序列 。
自注意力模型可以作为神经网络中的一层来使用,既可以用来替换卷积层和循环层,也可以和它们一起交替使用。
为了增强网络容量,我们可以 引入辅助记忆单元,将一些信息保存辅助记忆中,在需要时再进行读取,这样可以有效地增加网络容量 。这个引入辅助记忆单元一般称为 外部记忆(External Memory) ,以区别与循环神经网络的内部记忆(即隐状态)。
生理学家发现信息是作为一种 整体效应(collective effect) 存储在大脑组织中。当大脑皮层的不同部位损伤时,其导致的不同行为表现似乎取决于损伤的程度而不是损伤的确切位置。 大脑组织的每个部分似乎都携带一些导致相似行为的信息。也就是说,记忆在大脑皮层是分布式存储的,而不是存储于某个局部区域 。
人脑中的记忆具有 周期性 和 联想性 。
长期记忆可以类比于人工神经网络中的权重参数,而短期记忆可以类比于人工神经网络中的隐状态 。
除了长期记忆和短期记忆,人脑中还会存在一个“缓存”,称为 工作记忆(Working Memory) 。在执行某个认知行为(比如记下电话号码,算术运算)时,工作记忆是一个记忆的临时存储和处理系统,维持时间通常为几秒钟。
和之前介绍的LSTM中的记忆单元相比,外部记忆可以存储更多的信息,并且不直接参与计算,通过读写接口来进行操作。而 LSTM模型中的记忆单元包含了信息存储和计算两种功能,不能存储太多的信息。因此,LSTM中的记忆单元可以类比于计算机中寄存器,而外部记忆可以类比于计算机中的存储器:内存、磁带或硬盘等 。
借鉴人脑中工作记忆,可以在神经网络中引入一个外部记忆单元来提高网络容量。 外部记忆的实现途径有两种:一种是结构化的记忆,这种记忆和计算机中的信息存储方法比较类似,可以分为多个记忆片段,并按照一定的结构来存储;另一种是基于神经动力学的联想记忆,这种记忆方式具有更好的生物学解释性 。
一个不太严格的类比表格如下:
为了增强网络容量,一种比较简单的方式是引入结构化的记忆模块, 将和任务相关的短期记忆保存在记忆中,需要时再进行读取 。这种装备外部记忆的神经网络也称为 记忆网络(Memory Network,MN) 或 记忆增强神经网络(Memory Augmented Neural Network,MANN) 。
记忆网络结构如图:
一般有以下几个模块构成:
这种结构化的外部记忆是带有地址的,即每个记忆片段都可以按地址读取和写入。要实现类似于人脑神经网络的联想记忆能力,就需要按内容寻址的方式进行定位,然后进行读取或写入操作。 按内容寻址通常使用注意力机制来进行。通过注意力机制可以实现一种“软性”的寻址方式,即计算一个在所有记忆片段上的分布,而不是一个单一的绝对地址 。比如读取模型 的实现方式可以为:
其中 是主网络生成的查询向量, 为打分函数。类比于计算机的存储器读取, 计算注意力分布的过程相当于是计算机的“寻址”过程,信息加权平均的过程相当于计算机的“内容读取”过程 。因此,结构化的外部记忆也是一种联想记忆,只是其结构以及读写的操作方式更像是受计算机架构的启发。
通过引入外部记忆,可以将神经网络的参数和记忆容量的“分离”,即在少量增加网络参数的条件下可以大幅增加网络容量。 注意力机制可以看做是一个接口,将信息的存储与计算分离 。
端到端记忆网络(End-To-End Memory Network,MemN2N) 采用一种可微的网络结构,可以多次从外部记忆中读取信息。 在端到端记忆网络中,外部记忆单元是只读的 。
给定一组需要存储的信息 ,首先将其转换成两组记忆片段 和 ,分别存放在两个外部记忆单元中,其中 用来进行寻址, 用来进行输出。
主网络根据输入 生成 ,并使用注意力机制来从外部记忆中读取相关信息 :
并产生输出:
其中 为预测函数。当应用到分类任务时, 可以设为softmax 函数。
为了实现更新复杂的计算,我们可以让主网络和外部记忆进行多轮交互。在第 轮交互中,主网络根据上次从外部记忆中读取的信息 ,产生新的查询向量:
其中 为初始的查询向量, 。
假设第 轮交互的外部记忆为 和 ,主网络从外部记忆读取信息为:
端到端记忆网络结构如图:
External Attention:外部注意力机制
External Attention:外部注意力机制
作者: elfin
最近Transformer在CV领域的研究非常热,如ViT、BoTNet、External Attention等。使用Transformer的传统印象就是慢,这种慢还往往是我们不能接受的推理速度。在最近的实验中,基于单张2080TI,使用ResNet-34实现了batch_size为\\(288\\),图片大小为\\(32\\times200\\),每个epoch的训练用时大约为:5个小时;同样的实验环境下,我实验了Swin Transformer的结构,在stage1实验卷积进行下采样(实现embedding的效果),stage2~stage4使用Swin block,block的数量分别为[2, 8, 2],stage5使用两层卷积进行简单的任务适配。这个结构在训练时,batch_size设置到\\(42\\),图片大小修改为\\(32\\times240\\),每个epoch的训练用时大约为17个小时。Swin Transformer原作者声称其比卷积网络性能好,速度快,经过实验,实际上CNN的推理速度要比Transformer快,性价比方面Transformer确实是更高一些,但是其庞大的参数量也导致模型不太好训练。经过实验对比,在我的数据集上,Swin Transformer提升了将近7个百分点(epoch较少)。
虽然自注意力有那么多优点,但是这推理速度慢,耗资源的特点让我们这些缺硬件的渣渣很难受,然后就在前几天,突然看见清华、谷歌等大佬团队在做\\(Transformer\\rightarrow MLP\\)的操作,当然这里不是指简单返祖现象,以清华的工作为例,它将二次复杂度降到线性复杂度,这个特性有成功吸引到我,所以,下面是清华的External Attention的相关情况。
1、External Attention
1.1 自注意力机制
首先回顾 self-attention机制,常见的自注意力如图所示:
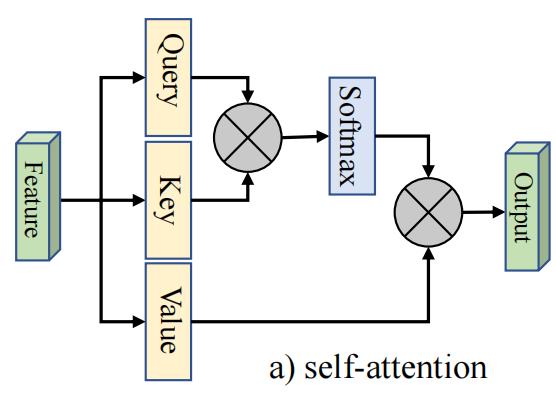
对于给定的输入特征图\\(F\\in \\mathbb{R}^{N\\times d}\\),其中\\(N\\)是像素个数,\\(d\\)是特征维度;自注意力产生了查询矩阵\\(Q\\in \\mathbb{R}^{N\\times {d}\'}\\),键矩阵\\(K\\in \\mathbb{R}^{N\\times {d}\'}\\),和值矩阵\\(V\\in \\mathbb{R}^{N\\times d}\\)。则自注意力机制的计算公式为:
简化版的注意力机制如下:
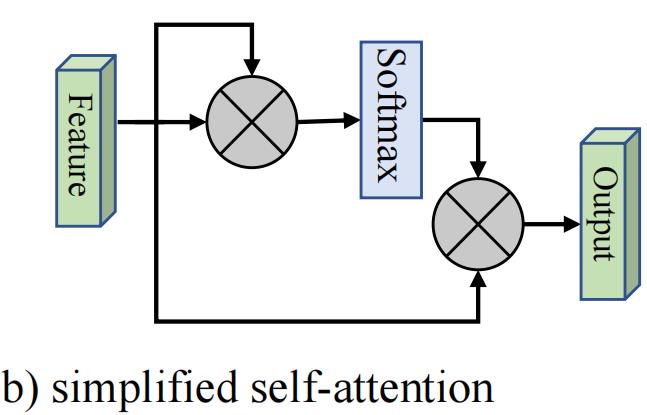
它的计算公式为:
基于上面的公式不难发现,注意力特征图是计算像素级的相似度,输出是输入的精确特征表示。
即使公式(3)(4)简化了,但是其计算复杂度仍然是\\(O\\left ( dN^{2} \\right )\\)。我们注意到随着特征图的增大,计算量的增大往往是我们无法接受的。以我上面的实验为例:
- \\(32\\times200\\)的计算量为:\\(192\\times\\left ( 32\\times200 \\right )^{2}=7864320000\\)
- \\(32\\times240\\)的计算量为:\\(192\\times\\left ( 32\\times240 \\right )^{2}=11324620800\\)
大约增加了\\(40\\%\\)的计算量,这还只是一层,当然上面的计算方式有待商榷,但这也说明了计算量的增长是非常迅猛的,而且在高级语义特征图中,通道数会更大,一定程度上几乎会导致在所有层级上计算量都有很大的提升。当然这个增长是呈现指数倍率增长,所以我们需要提升精度的同时,提升速度、优化资源占用。
1.2 外部注意力机制
经过实验得知:自注意力机制是一个\\(N-to-N\\)的注意力矩阵,可视化像素之间的关系,可以发现这种相关性是比较稀疏的,即很多是冗余信息。因此清华团队提出了一个外部注意力模块。
它的注意力计算是在输入像素与一个外部记忆单元\\(M\\in \\mathbb{R}^{S\\times d}\\)之间:
注意与自注意力机制不同,上式(5)是第\\(i\\)个像素点与\\(M\\)第\\(j\\)行的相似度。这里\\(M\\)是一个输入Input的可学习相关性参数,作为训练数据集的全局记忆。\\(A\\)是从先验信息得来的注意力特征图,Norm操作和自注意力一样。最终,通过\\(A\\)来更新\\(M\\)。
另外,我们用两种不同的记忆单元:\\(M_{k}\\)和\\(M_{v}\\)来增加网络的建模能力。
最终外部注意力机制的计算公式为:
经过上面的公式,外部注意力机制的复杂度是\\(O(dSN)\\)。这里的\\(d\\)、\\(S\\)是一个超参数,经过实验,作者发现\\(S\\)设置为64效果挺好。因此外部注意力机制比自注意力机制更高效,并且它可以直接应用于大尺寸的输入。
2、思考
- 计算量的降低和特征图的大小关系很大,这里的外部注意力机制的\\(S\\)设置为64,那么特征图的像素个数低于64时,实际它的计算量就更大。
- Swin Transformer是基于窗口进行自注意力计算的,window size作者使用的是7,像素个数\\(N=49\\),这也小于\\(64\\),所以同等情况下,外部注意力会有更大的计算量。
完!
以上是关于注意力机制与外部记忆的主要内容,如果未能解决你的问题,请参考以下文章