平衡查找树

Posted 2020-09-21 我是老邱

一、2-3查找树

二叉查找树可以使用于大多数应用场景，但是最坏情况下性能太差。

本节将介绍一种二分查找树，它的运行时间可以保证在对数级别内。

 

1、定义

这里引进3-节点的概念，3-节点含有两个键和三个链接。

2-节点是标准二叉查找树中的节点，含有一个键和两个链接。

Definition.

 A 2-3 search tree is a tree that either is empty or:

• A 2-node, with one key (and associated value) and two links, a left link to a 2-3 search tree with smaller keys, and a right link to a 2-3 search tree with larger keys
• A 3-node, with two keys (and associated values) and three links, a left link to a 2-3 search tree with smaller keys, a middle link to a 2-3 search tree with keys between the node\'s keys and a right link to a 2-3 search tree with larger keys.

 

示意图：

 

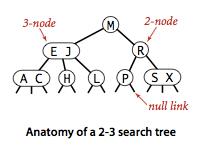
一棵完美平衡的2-3查找树中所有空链接到根节点的距离应该都是相同的。

后续将用2-3树来指代完美平衡的2-3查找树。

 

2、查找操作

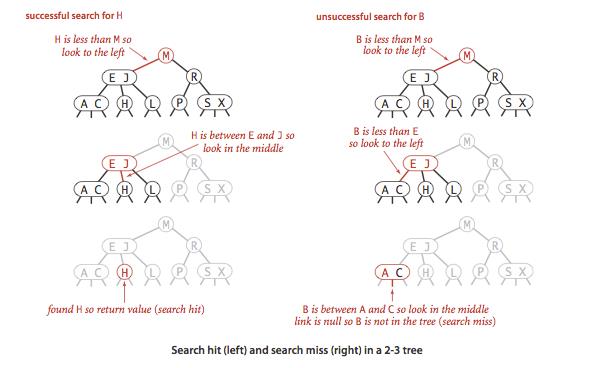
将二叉查找树的查找方法一般化即可得到2-3查找树的查找方法。

（1）先将键值跟根节点中的键进行比较，如果和任意一个键值相等，则查找命中。

（2）否则，根据比较的结果，找到相应区间的链接，并在其指定的子树中继续查找。

（3）如果这是个空链接，那么查找失败。

 

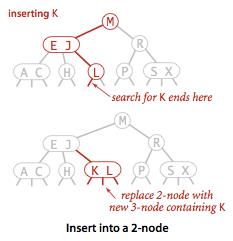
3、向2-节点中插入新键

要在2-3树中插入一个新的节点，我们可以向二叉查找树一样先进性一次未命中查找，然后把新节点挂在树的底部。

但是不能保证完美平衡性，需要在插入之后采取操作保持完美平衡性。

如果未命中的节点是2-节点，那么将这个键加入2-节点中组成3-节点。

如果未命中的节点是3-节点，那么需要采取更多措施。

 

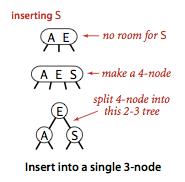
4、向一棵只有一个3-节点的树中插入新键

第一步先把新键临时存到该节点中，使之成为4-节点，有三个键和4个链接。

然后将其分解成3个2-节点组成的2-3树，含有中间键值的2-节点作为根节点，含有最小键值的2-节点跟根节点的左链接相连，含有最大键值的2-节点跟根节点的右链接相连。

插入键前树的高度为0，插入后树的高度为1，这个例子比较特殊，这是树增长的特殊案例。

 

 

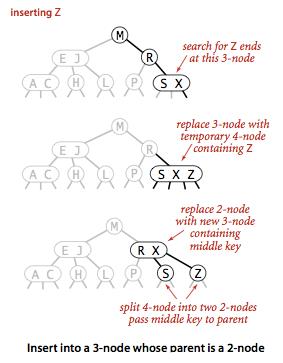
5、向一个父节点是2-节点的3-节点中插入新键

同样，先将新键临时保存到该节点中，组成4-节点并将其分解，但此时不会为中键创建一个新节点。

而是将中键移到父节点中，指向旧的3-节点的链接将被中键两边的两条链接替代，并分别指向两个新的2-节点。

这次转换并不影响2-3树的主要性质，树仍然是有序的，仍然是完美平衡的（空链接到根节点的距离仍然相同）。

 

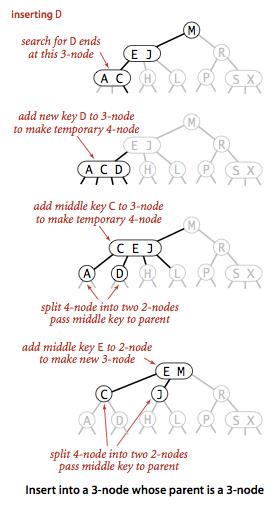
6、向一个父节点是3-节点的3-节点中插入新键

同样，先将新键临时保存到该节点中，组成4-节点再将其分解，将中键插入到父节点中，同时指向旧的3-节点的链接将被中键两边的两条链接替代，父节点此时成为临时的4-节点。

对新的4-节点进行同样的处理，即分解4-节点并将中键插入到父节点中。

推广到一般情况，我们就这样一直向上不断分解临时的4-节点直到遇到一个2-节点，并将其替换成一个3-节点，或者一直到3-节点的根。

 

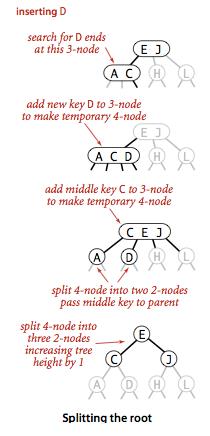
7、分解根节点

如果从插入节点到根节点一路都是3-节点，根节点最终将变成一个临时的4-节点。

这种情况可以照向一棵只有一个3-节点的树中插入新键的方法处理这个问题。

将根节点分解为3个2-节点，使得树高加1。

 

8、局部变换

将2-3树中的一个4-节点分解分解，有六种情况。4-节点是根节点，4-节点是2-节点的左子节点，4-节点是2-节点的右子节点，4-节点是3-节点左子节点，4-节点是3-节点中子节点，4-节点是3-节点右子节点。

2-3插入算法的根本是所有这些都是局部的，除了相关的节点和链接之外不必修改或者检查树的其他部分。

每一次变换中，变更的链接个数不会超过一个很小的常数。每个变换都会将4-节点中的一个键送入它的父节点并重构相应的链接而不用改树的其他部分。

 

9、全局性质

上述局部变换不会影响树的全局有序性和平衡性：任何空链接到根节点的路径长度都是相等的。

 

10、分析

结论：在一棵大小为N的2-3树中，查找和插入操作访问的节点必然不超过logN个。

证明：一棵大小为N的2-3树中，其高度在logN和log3N之间。

2-3树在最坏情况下仍有较好的性能，查找和插入的性能被保证在对数时间内。

但是这样直接实现2-3树不是很现实，因为有很多情况需要处理。

 

二、红黑二叉查找树

上述所述的2-3树插入算法并不难理解，但也不难实现。这里用一种简单的红黑二叉查找树数据结构来表达并实现。

 

 1、替换3-节点

红黑二叉查找树背后的基本思想是利用标准的二叉查找树（完全由2-节点构成）再通过添加一些额外的信息来表示3-节点从而实现2-3树。

红黑二叉查找树的链接有两种类型，红链接和黑链接。红链接将两个2-节点链接起来构成一个3-节点。黑链接是2-3树中的普通链接。

更加准确地表达是，3-节点是由一条左斜的红色链接相连的两个2-节点组成的，即其中一个2-节点是另一个2-节点的左子节点。

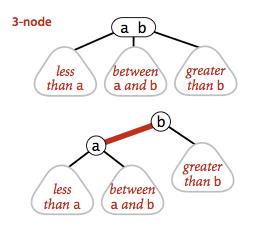
这样表示的优点就是，可以复用标准二叉查找树的方法，如get等。

用这种方式表示2-3树的二叉查找树称为红黑二叉查找树，简称红黑树。

 

2、等价定义

红链接均为左链接
没有任何节点能有两个红链接
该树是完美黑色平衡的：即任意空链接到根节点的路径上的黑链接数量相同

 

3、一一对应

红黑树>>2-3树

如果我们将红链接都展平，那么所有的空链接到根节点的距离都是相同的。

再将红链接相连的两个节点合并，那么就得到了一棵2-3树。

2-3树>>红黑树

如果将一棵2-3树中3-节点画作由红色左链接相连的两个2-节点，那么就不会存在有两个红链接的节点，而且树是完美黑色平衡的。

 

无论我们采用何种方式定义，红黑树都既是二叉查找树和2-3树。

只要能在保持一一对应关系的基础上实现2-3树的插入算法，就能结合两个算法的优点：二叉查找树中简洁高效的查找方法和2-3树中高效的平衡插入算法。

 

4、颜色表示

将链接的颜色保存节点数据类型中，用布尔类型来存储。

private class Node {
        private Key key;           // key
        private Value val;         // associated data
        private Node left, right;  // links to left and right subtrees
        private boolean color;     // color of parent link
        private int size;          // subtree count

        public Node(Key key, Value val, boolean color, int size) {
            this.key = key;
            this.val = val;
            this.color = color;
            this.size = size;
        }
    }

这里约定空链接为黑色链接。

用两个常量来设定红黑链接。

    private static final boolean RED   = true;
    private static final boolean BLACK = false;

 

实现一个判断链接是否红色的便捷方法，测试该节点的父链接是否为红色。

　　// is node x red; false if x is null ?
    private boolean isRed(Node x) {
        if (x == null) return false;
        return x.color == RED;
    }

 

5、旋转

在我们实现某个操作时，我们可以暂时允许出现红色右链接或者两条连续的红链接，但在完成这些操作前这些都需要被修复。

旋转操作会改变红链接的指向。

首先，假设有一个红色右链接，我们需要对其进行左旋转转化成左链接。

左旋转方法接受一条指向红黑树中的某个节点的链接h作为参数，并且默认这个节点的右链接是红色的，左链接是黑色的。

会对其进行相应的调整，返回一个链接，指向同一组键的子树，且其左链接为红链接，右链接为黑链接。

上述操作很好理解，只是将较小者作为根节点改为用较大者作为根节点。

步骤如下：

先用x保存较大节点
把h的右链接替换为x的左链接
把x的左链接替换为h
这时x作为即将返回的根节点

此时还需要对指向h和x的链接进行颜色调整
指向x的链接颜色继承原来指向h的颜色，指向h的颜色改为红色

此时还要对子树的size进行更改
x的size继承旧的h的size，h的size则重新计算

 

右旋转很好实现，只需要将左右对调过来即可，如下所示：

 

6、旋转重置父节点的链接

无论是左旋转还是右旋转，旋转操作都会返回一个链接，在旋转返回后算法需要用这个返回值来重置父节点中的相应链接。

h = rotateLeft(h);

 

这个操作可能会导致两条连续的红链接，算法会继续用旋转操作修正这种情况。

在插入新键时，我们可以使用旋转操作帮助我们保证2-3树和红黑树之间的一一对应关系。因为旋转操作可以保持红黑树的两个重要性质：有序性和完美平衡性。

 

旋转操作可以保持红黑树不存在两条连续的红链接和不存在红色的右链接，下边对各种情况进行分析。

 

7、向2-节点插入新键

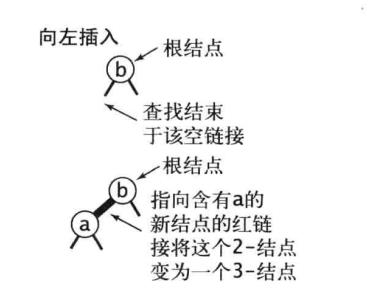
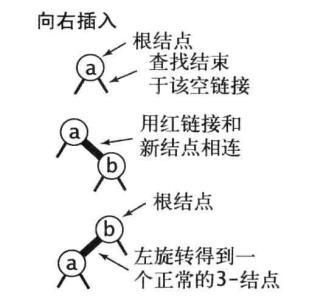
向一棵只有一个2-节点的红黑树中插入一个新的节点（红链接），如果新键小于2-节点中的键值，那么不用多余的操作。

如果新键大于2-节点中的键值，那么需要进行左旋转。

root = rotateLeft(root)

 

对根节点进行左旋转，并修正根节点的链接，图解：

 

8、向树底部2-节点中插入新键

用和二叉查找树相同的方法向一棵红黑树中插入一个新键，将会在底部新增一个节点。

但总是用红链接将新节点和父节点相连。如果父节点是一个2-节点，那么第7中的处理方法仍然适用。

如果指向新节点是父节点的左链接，那么父节点直接成为了一个3-节点。

如果指向新节点是父节点的右链接，那么需要进行一次左旋转。

 

9、向一个3-节点中插入新键

这种情况可以分为三种情况，新键小于3-节点中的两个键，新键在3-节点两个键之间，新键比3-节点两个键都要大。

这三种情况都会使一个节点同时链接到两个红链接。

 

最简单的是新键比3-节点两个键都要大的情况：

新节点被链接到3-节点的右链接，此时只需要将中键节点的两个红色链接改为黑色即可。

 

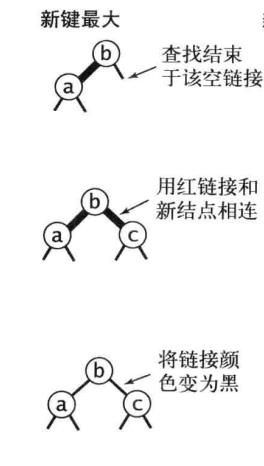
新键最小的情况：

新节点被链接到3-节点的左链接，产生了两条连续的红色链接。

此时只需对上层红色链接右旋转即可得到第一种情况。

 

 

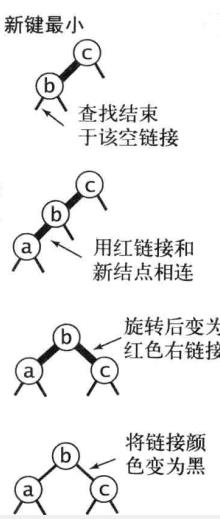
新键在3-节点两键之间的情况：

新节点链接到3-节点中的中间链接上，又产生了两条连续的红色链接。

此时将下层红链接左旋转即可得到第二种情况。

总的来说，最终得到的效果同2-3树中的切分临时4-节点。

转换成第一种情况之后，对中键节点进行颜色变换操作。

颜色变换的函数如下：

　　// flip the colors of a node and its two children
    private void flipColors(Node h) {
        // h must have opposite color of its two children
        // assert (h != null) && (h.left != null) && (h.right != null);
        // assert (!isRed(h) &&  isRed(h.left) &&  isRed(h.right))
        //    || (isRed(h)  && !isRed(h.left) && !isRed(h.right));
        h.color = RED;
        h.left.color = BLACK;
        h.right.color = BLACK;
    }

这里相当于将4-节点切分为3个2-节点，并将中键插入到父节点中。

颜色变换这个操作跟旋转操作一样都是局部变换，不会影响整棵树的黑色平衡性。

 

 

 

10、根节点总是为黑色

 上述的颜色变换操作可能会使根节点链接颜色变为红色，所以每次插入后都需要将根节点链接变为黑色。

 

11、红链接在树中向上传递

向树底部3-节点中插入新键，都会导致红链接向上传递，相当于将中键插入父节点中。

可以继续对父节点采取同样的修正操作，直到遇到2-节点或者根节点。

这种向上传递的处理，最好的实现方式是用递归的方法。

 

总之，只要准确地使用左旋转、右旋转和颜色变换这三种操作，就能保证插入操作后红黑树和2-3树的一一对应关系。

在沿着插入点到根节点路径向上移动时所经过的每个节点中顺序完成以下操作，就能完成插入操作：

如果右子节点是红色的，左子节点是黑色的，则进行左旋转
如果左子节点是红色的，并且它的左子节点也是红色的，则进行右旋转
如果左子节点和右子节点都是红色的，那么进行颜色变换

 

三、实现

因为保持树的平衡性的操作是自下而上的，植入已有的实现非常简单，只需要在递归调用之后执行这些操作即可。

/**
     * Inserts the specified key-value pair into the symbol table, overwriting the old 
     * value with the new value if the symbol table already contains the specified key.
     * Deletes the specified key (and its associated value) from this symbol table
     * if the specified value is {@code null}.
     *
     * @param key the key
     * @param val the value
     * @throws IllegalArgumentException if {@code key} is {@code null}
     */
    public void put(Key key, Value val) {
        if (key == null) throw new IllegalArgumentException("first argument to put() is null");
        if (val == null) {
            delete(key);
            return;
        }

        root = put(root, key, val);
        root.color = BLACK;
        // assert check();
    }

    // insert the key-value pair in the subtree rooted at h
    private Node put(Node h, Key key, Value val) { 
        if (h == null) return new Node(key, val, RED, 1);

        int cmp = key.compareTo(h.key);
        if      (cmp < 0) h.left  = put(h.left,  key, val); 
        else if (cmp > 0) h.right = put(h.right, key, val); 
        else              h.val   = val;

        // fix-up any right-leaning links
        if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
        if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
        if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);
        h.size = size(h.left) + size(h.right) + 1;

        return h;
    }

上述中的三个操作，都可以相应用一个if语句来完成。

代码相当简洁，但是如果没有2-3树和红黑树相关数据结构只是作为铺垫，这段实现将会非常难以理解。

 

四、删除

红黑树的 deleteMin()，deleteMax()和delete()函数实现比较麻烦。

要更好地描述删除算法，需要重回2-3树。

和插入操作一样，我们可以定义一系列局部变换来使删除一个节点的同时保持树的完美平衡性。

删除操作过程比插入过程稍微复杂一点，因为算法不仅要在沿着查找路径向下的同时进行构造临时4-节点，还要在沿着查找路径向上的同时进行分解临时4-节点（同插入操作）。

 

1、自顶向下的2-3-4树

作为第一轮热身，我们先了解一个沿查找路径既能向上也能向下进行变换的稍简单的插入算法。

2-3-4树插入算法：2-3-4树允许4-节点的存在，沿查找路径向下进行变换是为了保证当前节点不是4-节点，而沿查找路径向上进行变换是为了分解4-节点。

这个算法的实现：只需要移动一行代码即可。

/**
     * Inserts the specified key-value pair into the symbol table, overwriting the old 
     * value with the new value if the symbol table already contains the specified key.
     * Deletes the specified key (and its associated value) from this symbol table
     * if the specified value is {@code null}.
     *
     * @param key the key
     * @param val the value
     * @throws IllegalArgumentException if {@code key} is {@code null}
     */
    public void put(Key key, Value val) {
        if (key == null) throw new IllegalArgumentException("first argument to put() is null");
        if (val == null) {
            delete(key);
            return;
        }

        root = put(root, key, val);
        root.color = BLACK;
        // assert check();
    }

    // insert the key-value pair in the subtree rooted at h
    private Node put(Node h, Key key, Value val) { 
        if (h == null) return new Node(key, val, RED, 1);

        if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);

        int cmp = key.compareTo(h.key);
        if      (cmp < 0) h.left  = put(h.left,  key, val); 
        else if (cmp > 0) h.right = put(h.right, key, val); 
        else              h.val   = val;

        // fix-up any right-leaning links
        if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
        if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
        h.size = size(h.left) + size(h.right) + 1;

        return h;
    }
    

 

2、删除最小键

作为第二轮热身，我们分析2-3树中删除最小键的操作。

从树的底部的3-节点删除键时很简单的，但2-节点则很难，因为删除2-节点之后会留下一个空节点。这样会破坏树的完美平衡性。

为了保证算法不会删除2-节点，算法在沿着查找路径向下的同时，维持当前节点不是2-节点（3-节点或者临时的4-节点）。

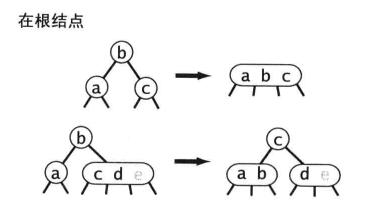
（1）根节点

有两种情况：

第一种情况：根节点以及其两个子节点都是2-节点，可以直接将这三个2-节点变为4-节点。

第二种情况：不是上述情况，有必要则从右侧兄弟节点中“借”一个键。

（2）沿着路径向下的时候

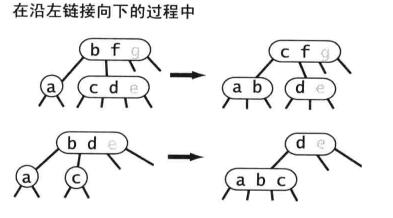
必须保持：

如果当前节点的左子节点不是2-节点，完成。

如果当前节点的左子节点是2-节点，且其临近节点不是2-节点，则将其临近节点中的一个键移到左子节点中。

如果当前节点的左子节点是2-节点，且其临近节点也是2-节点，则将左子节点、父节点最小键、临近节点组合成一个4-节点。父节点由3-节点变为2-节点或者由4-节点变为3-节点。

（3）底部

遍历这个过程，最终能得到一个含有最小键的3-节点或者4-节点。最后把最小键删除，再沿着查找路径向上分解所有临时4-节点。、

（4）实现

    /**
     * Removes the smallest key and associated value from the symbol table.
     * @throws NoSuchElementException if the symbol table is empty
     */
    public void deleteMin() {
        if (isEmpty()) throw new NoSuchElementException("BST underflow");

        // if both children of root are black, set root to red
        if (!isRed(root.left) && !isRed(root.right))
            root.color = RED;

        root = deleteMin(root);
        if (!isEmpty()) root.color = BLACK;
        // assert check();
    }

    // delete the key-value pair with the minimum key rooted at h
    private Node deleteMin(Node h) { 
        if (h.left == null)
            return null;

        if (!isRed(h.left) && !isRed(h.left.left))
            h = moveRedLeft(h);

        h.left = deleteMin(h.left);
        return balance(h);
    }

    // Assuming that h is red and both h.left and h.left.left
    // are black, make h.left or one of its children red.
    private Node moveRedLeft(Node h) {
        // assert (h != null);
        // assert isRed(h) && !isRed(h.left) && !isRed(h.left.left);

        flipColors(h);
        if (isRed(h.right.left)) { 
            h.right = rotateRight(h.right);
            h = rotateLeft(h);
            flipColors(h);
        }
        return h;
    }

     // restore red-black tree invariant
    private Node balance(Node h) {
        // assert (h != null);

        if (isRed(h.right))                      h = rotateLeft(h);
        if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
        if (isRed(h.left) && isRed(h.right))     flipColors(h);

        h.size = size(h.left) + size(h.right) + 1;
        return h;
    }

要特别注意的是，flipColors(Node h)是将三条链接的颜色反转，如下所示：

    // flip the colors of a node and its two children
    private void flipColors(Node h) {
        // h must have opposite color of its two children
        // assert (h != null) && (h.left != null) && (h.right != null);
        // assert (!isRed(h) &&  isRed(h.left) &&  isRed(h.right))
        //    || (isRed(h)  && !isRed(h.left) && !isRed(h.right));
        h.color = !h.color;
        h.left.color = !h.left.color;
        h.right.color = !h.right.color;
    }

删除操作这里，是将三个节点组合成临时4-节点，跟插入操作刚好反过来。

将上述沿着查找路径向下的分析中的2-3树一一对应到红黑树，可以更好地理解这段代码。

3、删除最大键

同样的道理，为了保证算法不会删除2-节点，算法在沿着查找路径向下的同时，维持当前节点不是2-节点（3-节点或者临时的4-节点）。

    /**
     * Removes the largest key and associated value from the symbol table.
     * @throws NoSuchElementException if the symbol table is empty
     */
    public void deleteMax() {
        if (isEmpty()) throw new NoSuchElementException("BST underflow");

        // if both children of root are black, set root to red
        if (!isRed(root.left) && !isRed(root.right))
            root.color = RED;

        root = deleteMax(root);
        if (!isEmpty()) root.color = BLACK;
        // assert check();
    }

    // delete the key-value pair with the maximum key rooted at h
    private Node deleteMax(Node h) { 
        if (isRed(h.left))
            h = rotateRight(h);

        if (h.right == null)
            return null;

        if (!isRed(h.right) && !isRed(h.right.left))
            h = moveRedRight(h);

        h.right = deleteMax(h.right);

        return balance(h);
    }

    // Assuming that h is red and both h.right and h.right.left
    // are black, make h.right or one of its children red.
    private Node moveRedRight(Node h) {
        // assert (h != null);
        // assert isRed(h) && !isRed(h.right) && !isRed(h.right.left);
        flipColors(h);
        if (isRed(h.left.left)) { 
            h = rotateRight(h);
            flipColors(h);
        }
        return h;
    }

这里跟删除最小键有点不同，因为我们认为规定了3-节点是红链接左斜的。

4、删除

在向下查找路径中：

如果在左树，跟删除最小键一样的变换操作可以保证当前节点不是2-节点。

如果在右树，跟删除最大键一样的变换操作可以保证当前节点不是2-节点。

如果被查找的键在树的底部，可以直接删除。

如果不是在底部，算法需要将它和它的继承节点交换（和经典二叉查找树一样），问题转换为在一棵根节点不是2-节点的子树中删除最小键。

    // delete the key-value pair with the given key rooted at h
    private Node delete(Node h, Key key) { 
        // assert get(h, key) != null;

        if (key.compareTo(h.key) < 0)  {
            if (!isRed(h.left) && !isRed(h.left.left))
                h = moveRedLeft(h);
            h.left = delete(h.left, key);
        }
        else {
            if (isRed(h.left))
                h = rotateRight(h);
            if (key.compareTo(h.key) == 0 && (h.right == null))
                return null;
            if (!isRed(h.right) && !isRed(h.right.left))
                h = moveRedRight(h);
            if (key.compareTo(h.key) == 0) {
                Node x = min(h.right);
                h.key = x.key;
                h.val = x.val;
                // h.val = get(h.right, min(h.right).key);
                // h.key = min(h.right).key;
                h.right = deleteMin(h.right);
            }
            else h.right = delete(h.right, key);
        }
        return balance(h);
    }

五、性质分析

性质1：一棵大小为N的红黑树的高度不会超过2logN。

简略证明：最坏情况是其最左边的节点全部是3-节点，而其余均为2-节点。

 

性质2：一棵大小为N的红黑树中，根节点到任意节点的平均路径长度为~1.00logN。

 

红黑树最复杂的代码仅限于put和delete，二叉查找树中的其余方法可以不用改动就可以使用。

红黑树保证了所有的操作运行时间都是对数级别的。