输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5

Posted 2020-09-21 洞拐洞幺

问题描述：

　　　　输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

　　思路：

　　在二叉树的前序遍历序列中，第一个数字总是树的根结点的值。但在中序遍历序列中，根结点的值在序列的中间，左子树的结点的值位于根结点的值的左边，而右子树的结点的值位于根结点的值的右边。因此我们需要扫描中序遍历序列，才能找到根结点的值。

　　如下图所示，前序遍历序列的第一个数字1就是根结点的值。扫描中序遍历序列，就能确定根结点的值的位置。根据中序遍历特点，在根结点的值1前面的3个数字都是左子树结点的值，位于1后面的数字都是右子树结点的值。

 

 

　　

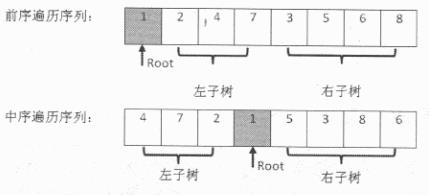
　　同样，在前序遍历的序列中，根结点后面的3个数字就是3个左子树结点的值，再后面的所有数字都是右子树结点的值。这样我们就在前序遍历和中序遍历两个序列中，分别找到了左右子树对应的子序列。

　　既然我们已经分别找到了左、右子树的前序遍历序列和中序遍历序列，我们可以用同样的方法分别去构建左右子树。也就是说，接下来的事情可以用递归的方法去完成。
　　完整的代码示例如下，方式一使用数组存储前序遍历序列和中序遍历序列；方式二使用容器存储。

#include<iostream>  
using namespace std;  
  
template<class T>  
struct BinaryTreeNode  
{  
    T _value; //数据  
    BinaryTreeNode<T>* _left; //左孩子  
    BinaryTreeNode<T>* _right; //右孩子  
  
    BinaryTreeNode()  
        : _value()  
        , _left(NULL)  
        , _right(NULL)  
    {}  
      
};  
template<class T>  
class BinaryTree  
{  
public:   
    BinaryTreeNode<T>* ConstructCore(int* startPre,int* endPre,int* startIn,int* endIn)  
    {  
        int rootValue = startPre[0];  //前序遍历的第一个数字就是根节点的值  
        BinaryTreeNode<T>* root = new BinaryTreeNode<T>();   
        root->_value = rootValue;  
        root->_left = root->_right = NULL;  
        cout << root->_value<< " ";  
  
        if (startPre == endPre)  
        {  
            if (startIn == endIn && *startPre == *startIn)  
            {  
                return root;  
            }  
            else  
            {  
                return NULL;  
            }  
        }  
  
        int* rootIn = startIn;  
        //在中序遍历中找根节点的值  
        while (*rootIn != rootValue && rootIn <= endIn)  
        {  
            ++rootIn;  
        }  
        if (rootIn == endIn && *rootIn != rootValue)  
            return NULL;  
          
        int leftLength = rootIn - startIn;//左子树长度   中序遍历序列中根节点前面的数字都是左子树节点的值  
        int* leftEnd = startPre + leftLength;//前序遍历序列中左子树的值  
        //构建左子树  
        if (leftLength > 0)  
        {  
            root->_left=ConstructCore(startPre+1,leftEnd,startIn,rootIn-1);  
        }  
        //构建右子树  
        if (leftLength < endPre - startPre)  
        {  
            root->_right = ConstructCore(leftEnd+1,endPre,rootIn+1,endIn);  
        }  
        return root;      
    }  
    BinaryTreeNode<T>* Construct(int* preorder, int* inorder, int length)  
    {  
        if (preorder == NULL || inorder == NULL || length <= 0)  
            return NULL;  
        return ConstructCore(preorder,preorder+length-1,inorder,inorder+length-1);  
    }     
};  
  
int main()  
{  
    int preorder[] = { 1,2,4,7,3,5,6,8 };  
    int inorder[] = { 4,7,2,1,5,3,8,6 };  
    BinaryTree<int> bt;  
    BinaryTreeNode<int>* root=bt.Construct(preorder, inorder, 8);  
    return 0;  
}