数据结构基本概念

Posted 2020-09-21 在下雨的Tokyo

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构基本概念相关的知识，希望对你有一定的参考价值。

什么是数据结构

“数据结构是数据对象，以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出”——Sartaj Sahni,《数据结构、算法与应用》
“数据结构是ADT(抽象数据类型Abstract Data Type)的物理实现。”——Clifford A.Shaffer,《数据结构与算法分析》
“数据结构(data structture)是计算机中存储、组织数据的方式。通常情况下，经i想你选择的数据结构可以带来最优效率的算法。”——中文维基百科

　目前没有官方的定义。

思考：解决问题方法的效率，跟什么有关呢？

① 解决问题方法的效率，跟数据的组织方式有关

例1：如何在书架上摆放书籍？

首先这个问题是不科学的，没有告诉书架的是什么样子的。

图书的摆放要使得2个相关操作方便实现：

操作1：新书怎么插入？
操作2：怎么找到某本指定的书？

解决方法：

方法1：随便放
- 操作1：新书怎么插入？
  - 哪里有空放哪里，一步到位
- 操作2：怎么找到某本指定的书？
  - 累死......
方法2：按照书名的拼音字母顺序排放
- 操作1：新书怎么插入？
- 操作2：怎么找到某本指定的书？
  - 二分查找
方法3：把书架划分成几块区域，每块区域指定摆放某种类别的图书，在每种类别内，按照书名的拼音字母顺序排放
- 操作1：新书怎么插入？
  - 先定类别，二分查找确定位置，移出空位
- 操作2：怎么找到某本指定的书？
  - 先定类别，再二分查找

问题来了：空间如何分配？类别应该分多细？

② 解决问题方法的效率，跟空间的利用效率有关。

例2：写程序实现一个函数PrintN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数。

两种不同的实现方式：

循环实现的函数：                       
void PrintN(int N){                 
  int i;                                
  for(i=1;i<=N;i++){                    
    printf("%d ",i);                    
  }                                     
}

1 递归实现的函数：
2 void PrintN(int N){
3     if(N){
4        PrintN(N-1);
5        Printf("%d ",i);
6     }
7 }

如何比较这两个函数的执行效率呢？不妨将N=100，1000，10000，100000，......

测试程序：

#include<stdio.h>
void PrintN(int N);
int main(){
    int N;
    scanf("%d",&N);
    PrintN(N);
    return 0;  
}

当N=100时：(经测试，N=10，100，1000，两个函数的显示都是正常的)

当N=100000时，显示出问题：循环实现的函数运行正常，但是递归实现的函数无法运行。

递归函数虽然简单、容易理解，但是对空间的占用率大，一般电脑不会选择执行递归的程序，当它将所有能利用的空间占用后，就直接爆掉，所以在N等于100000时，没有任何输出。

③ 解决问题方法的效率，跟算法的巧妙程度有关

例3：写程序计算给定多项式在给定点x处的值。f(x)=a₀+a₁x+...+a_n-1x^n-1+a_nxⁿ

最傻最直接的算法：对标准多项式的一个直接翻译

1 double f(int n,double a[],double x){
2     int i;
3     double p=a[0];
4     for(i=1;i<=n;i++){
5         p+=(a[i]*pow(x,i));//累加求和
6     }
7     return p;
8 }

这种写法比较low，专业处理方式：利用结合律，将函数的形式改成：f(x)=a₀+x(a₁+x(...(a_n-1+x(a_n))))

处理这个问题的标准程序：

1 double f(int n,double a[],double x){
2     int i;
3     double p=a[n];
4     for(i=n;i>0;i--){
5         p=a[i-1]+x*p;
6     }
7     return p;
8 }

凭什么说第二个函数比第一个函数要好呢？——当然是因为第二个函数的执行效率高啦！C语言里面提供了clock()这个函数用于测试。

clock()：捕捉从程序开始运行到clock()被调用所耗费的时间。这个时间单位是clock tick,即“时钟打点”。

配套的常数CLK_TCK：机器时钟每秒所走的时钟打点数。【不同的机器可能不一样】

常用的测试模板

#include<stdio.h>
#include<time.h>   //需要引入这个头文件

clock_t start,stop;
/* clock_t是clock()函数返回的变量类型 */
double duration;
/* 记录被测函数运行时间，以秒为单位 */
int main(){
    /* 不在测试范围内的准备工作写在clock()调用之前 */
    start=clock();//开始计时
    MyFunction(); //被测函数写在这里
    stop=clock(); //停止计时
    duration=((double)(stop-start))/CLK_TCK;//换算成以秒为单位
　　 /* 其他不在测试范围内的处理写在后面，例如输出duration的值 */
    return 0;
}

下面我们写程序计算多项式在给定点x=1.1处的值f(1.1)

测试程序：

 1 #include<stdio.h>
 2 #include<math.h>
 3 #include<time.h>
 4 clock_t start,stop;
 5 double duration;
 6 #define MAXN 10  //多项式最大项数，即多项式阶数+1
 7 double f1(int n,double a[],double x);
 8 double f2(int n,double a[],double x);
 9 int main(){
10     int i;
11     double a[MAXN];//存储多项式的系数
12     for(i=0;i<MAXN;i++)
13         a[i]=(double)i;
14     start=clock();
15 
16     f1(MAXN-1,a,1.1);
17     stop=clock();
18     duration=((double)(stop-start))/CLK_TCK;
19     printf("ticks1=%f\\n",(double)(stop-start));
20     printf("duration1=%6.2fe\\n",duration);
21 
22     start=clock();
23     f2(MAXN-1,a,1.1);
24     stop=clock();
25     duration=((double)(stop-start))/CLK_TCK;
26     printf("ticks2=%f\\n",(double)(stop-start));
27     printf("duration2=%6.2fe\\n",duration);
28 
29     return 0;
30 }
31 
32 
33 double f1(int n,double a[],double x){
34      int i;
35      double p=a[0];
36      for(i=1;i<=n;i++){
37          p+=(a[i]*pow(x,i));//累加求和
38      }
39      return p;
40  } 
41 double f2(int n,double a[],double x){
42      int i;
43      double p=a[n];
44      for(i=n;i>0;i--){
45          p=a[i-1]+x*p;
46      }
47      return p;
48  }

结果：

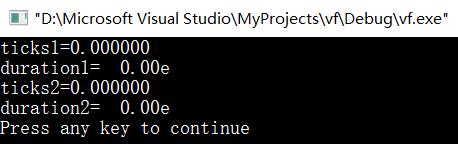
原因：两个函数的运行速度太快，都不满足一个tick，clock函数根本捕捉不到两个函数的区别

解决方案：让被测函数重复运行充分多次，使得测出的总的时钟打点间隔充分长，最后计算被测函数平均每次运行的时间即可！

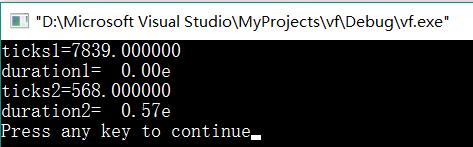
 1 ......
 2 #define MAXK 1e7 //被测函数最大重复次数
 3 ......
 4 int main(){
 5     ......
 6     start=clock();
 7     for(i=0;i<MAXK;i++)
 8         f1(MAXN-1,a,1.1);
 9     stop=clock();
10     duration=((double)(stop-start))/CLK_TCK/MAXK;//计算单次运行时间
11     printf("ticks1=%f\\n",(double)(stop-start));
12     printf("duration1=%6.2fe\\n",duration);
13         ......
14     return 0;
15 }
16 ......