决策树算法

Posted 2020-09-20

1、决策树/判定树

决策树/判定树是一个类似于流程图的树结构，其中每个内部结点表示在一个属性上的测试，每个分支表示一个属性输出，而每个树叶结点代表类或者类分布。树的最顶层是根节点

如下图所示，根节点为Play 9 + Don‘t Play 5，根据OUTLOOK属性产生三个分支sunny、overcast、rain，其中为overcast时产生一个类，即Play 4 + Don‘t Play 0，为sunny和rain时还要继续根据其他属性来做划分。

 

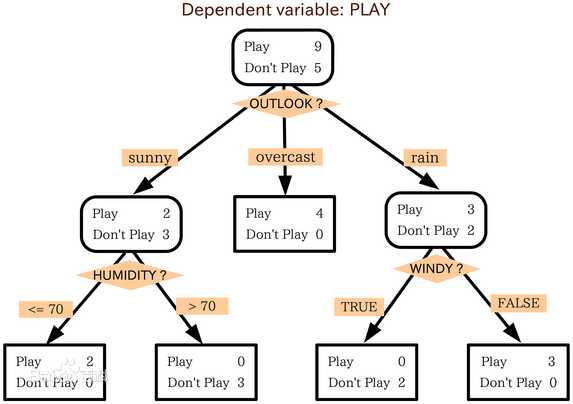
2、决策树构造

决策树的构造过程不依赖领域知识，它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。

构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况：

1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。

2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试，按照“属于此子集”和“不属于此子集”分成两个分支。

3、属性是连续值。此时确定一个值作为分裂点split_point，按照>split_point和<=split_point生成两个分支。

构造决策树的关键性内容是进行属性选择度量，属性选择度量是一种选择分裂准则，是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式方法，它决定了拓扑结构及分裂点split_point的选择。

 

3、ID3算法

• 树以代表训练样本的单个结点开始。
• 如果样本都在同一个类，则该结点成为树叶，并用该类标号。
• 否则，算法使用称为信息增益的基于熵的度量作为启发信息，选择能够最好地将样本分类的属性。该属性成为该结点的“测试”或“判定”属性。在算法的该版本中，所有的属性都是分类的，即离散值。连续属性必须离散化。对测试属性的每个已知的值，创建一个分枝，并据此划分样本。算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不必在该结点的任何后代上考虑它。

• 递归划分步骤仅当下列条件之一成立停止：

　　(a) 给定结点的所有样本属于同一类。

　　(b) 没有剩余属性可以用来进一步划分样本。在此情况下，使用多数表决。这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结点样本的类分布。

　　(c) 分枝test_attribute = ai没有样本。在这种情况下，以 samples 中的多数类创建一个树叶。

 

几个相关概念：

　　1、设D为用类别对训练元组进行的划分，则D的熵（entropy）表示为：

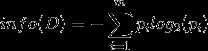
 　　其中pi表示第i个类别在整个训练元组中出现的概率，可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。

　　2、假设将训练元组D按属性A进行划分，则A对D划分的期望信息为：

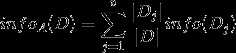
　　3、信息增益即为两者的差值：

 

 

 

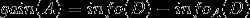
举例，如下图所示：

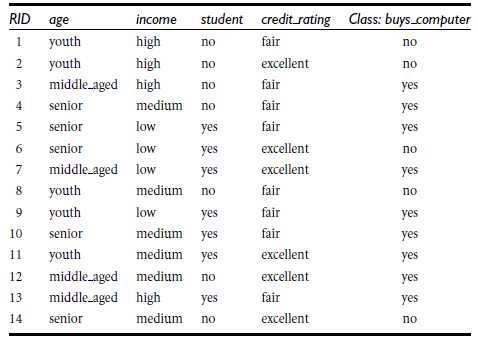
 其中，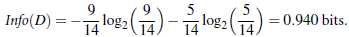

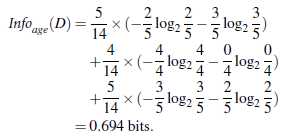
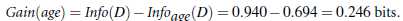
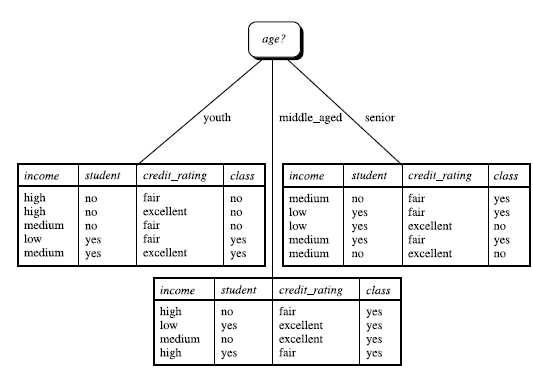
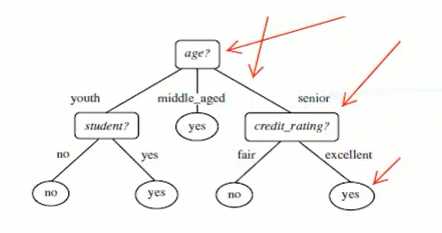
 类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048。因此选择age作为根节点，即

重复上述步骤，直至满足停止条件。结果为：                                                              分支                根节点     结点             树叶

4、C4.5算法

ID3算法存在一个问题，就是偏向于多值属性，例如，如果存在唯一标识属性ID，则ID3会选择它作为分裂属性，这样虽然使得划分充分纯净，但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率（gain ratio）的信息增益扩充，试图克服这个偏倚。

C4.5算法首先定义了“分裂信息”，其定义可以表示成：

?

 

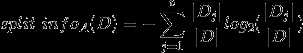
其中各符号意义与ID3算法相同，然后，增益率被定义为：

?

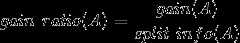
C4.5选择具有最大增益率的属性作为分裂属性，其具体应用与ID3类似。