逻辑回归特征选择

Posted 2020-09-20 msw0529

特征选择很重要，除了人工选择，还可以用
其他机器学习方法，如逻辑回归、随机森林、PCA、
LDA等。

分享一下逻辑回归做特征选择

特征选择包括:

特征升维

特征降维

特征升维

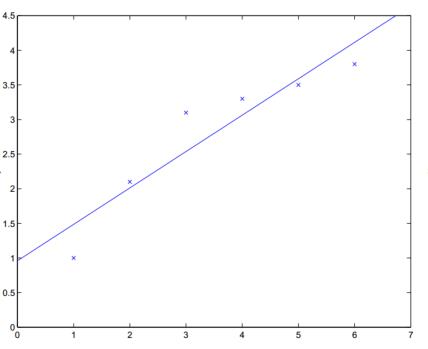
如一个样本有少量特征，可以升维，更好的拟合曲线

 

特征X 

 

升维X/X**2/

效果验证，做回归

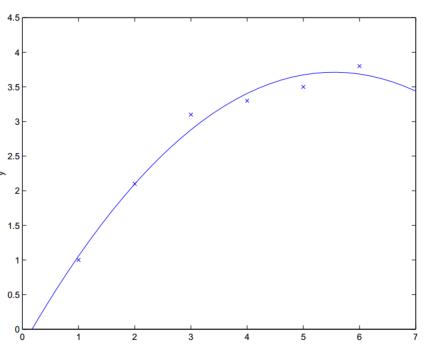
加特征x**2之后的效果

 

 

 

特征X1、X2 

升维X1/X2/X1X2/X1**2/X2**2/  

 

 特征降维

利用L1正则化做特征选择

sparkmllib代码实现

import java.io.PrintWriter
import java.util

import org.apache.spark.ml.attribute.{Attribute, AttributeGroup, NumericAttribute}
import org.apache.spark.ml.classification.{BinaryLogisticRegressionTrainingSummary, LogisticRegressionModel, LogisticRegression}
import org.apache.spark.mllib.classification.LogisticRegressionWithSGD
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.rdd.RDD
import org.apache.spark.sql.{SQLContext, DataFrame, Row}
import org.apache.spark.sql.types.{DataTypes, StructField}
import org.apache.spark.{SparkContext, SparkConf}

object LogisticRegression {
    def main(args: Array[String]) {
        val conf = new SparkConf().setAppName("test").setMaster("local")
        val sc = new SparkContext(conf)
        val sql  = new SQLContext(sc);
        val df: DataFrame = sql.read.format("libsvm").load("rl.txt")

//        val training = sc.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")


        val Array(train, test) = df.randomSplit(Array(0.7, 0.3),seed = 12L)
        val lr = new LogisticRegression()
                .setMaxIter(10)
                .setRegParam(0.3)
                .setElasticNetParam(1)//默认0 L2   1---》L1

        // Fit the model
        val lrModel: LogisticRegressionModel = lr.fit(train)

        lrModel.transform(test).show(false)
        // Print the coefficients and intercept for logistic regression
//        coefficients 系数  intercept 截距
        println(s"Coefficients: ${lrModel.coefficients} Intercept: ${lrModel.intercept}")

        lrModel.write.overwrite().save("F:\\\\mode")

        val weights: Array[Double] = lrModel.weights.toArray

        val pw = new PrintWriter("F:\\\\weights");
        //遍历
        for(i<- 0 until weights.length){
            //通过map得到每个下标相应的特征名

            //特征名对应相应的权重
            val str = weights(i)
            pw.write(str.toString)
            pw.println()
        }
        pw.flush()
        pw.close()


    }
}

　　样本lr.txt

0 1:5.1 2:3.5 3:1.4 4:0.2
0 1:4.9 2:3.0 3:1.4 4:0.2
0 1:4.7 2:3.2 3:1.3 4:0.2
0 1:4.6 2:3.1 3:1.5 4:0.2
0 1:5.0 2:3.6 3:1.4 4:0.2
0 1:5.4 2:3.9 3:1.7 4:0.4
0 1:4.6 2:3.4 3:1.4 4:0.3
0 1:5.0 2:3.4 3:1.5 4:0.2
0 1:4.4 2:2.9 3:1.4 4:0.2
0 1:4.9 2:3.1 3:1.5 4:0.1
0 1:5.4 2:3.7 3:1.5 4:0.2
0 1:4.8 2:3.4 3:1.6 4:0.2
0 1:4.8 2:3.0 3:1.4 4:0.1
0 1:4.3 2:3.0 3:1.1 4:0.1
0 1:5.8 2:4.0 3:1.2 4:0.2
0 1:5.7 2:4.4 3:1.5 4:0.4
0 1:5.4 2:3.9 3:1.3 4:0.4
0 1:5.1 2:3.5 3:1.4 4:0.3
0 1:5.7 2:3.8 3:1.7 4:0.3
0 1:5.1 2:3.8 3:1.5 4:0.3
0 1:5.4 2:3.4 3:1.7 4:0.2
0 1:5.1 2:3.7 3:1.5 4:0.4
0 1:4.6 2:3.6 3:1.0 4:0.2
0 1:5.1 2:3.3 3:1.7 4:0.5
0 1:4.8 2:3.4 3:1.9 4:0.2
0 1:5.0 2:3.0 3:1.6 4:0.2
0 1:5.0 2:3.4 3:1.6 4:0.4
0 1:5.2 2:3.5 3:1.5 4:0.2
0 1:5.2 2:3.4 3:1.4 4:0.2
0 1:4.7 2:3.2 3:1.6 4:0.2
0 1:4.8 2:3.1 3:1.6 4:0.2
0 1:5.4 2:3.4 3:1.5 4:0.4
0 1:5.2 2:4.1 3:1.5 4:0.1
0 1:5.5 2:4.2 3:1.4 4:0.2
0 1:4.9 2:3.1 3:1.5 4:0.1
0 1:5.0 2:3.2 3:1.2 4:0.2
0 1:5.5 2:3.5 3:1.3 4:0.2
0 1:4.9 2:3.1 3:1.5 4:0.1
0 1:4.4 2:3.0 3:1.3 4:0.2
0 1:5.1 2:3.4 3:1.5 4:0.2
0 1:5.0 2:3.5 3:1.3 4:0.3
0 1:4.5 2:2.3 3:1.3 4:0.3
0 1:4.4 2:3.2 3:1.3 4:0.2
0 1:5.0 2:3.5 3:1.6 4:0.6
0 1:5.1 2:3.8 3:1.9 4:0.4
0 1:4.8 2:3.0 3:1.4 4:0.3
0 1:5.1 2:3.8 3:1.6 4:0.2
0 1:4.6 2:3.2 3:1.4 4:0.2
0 1:5.3 2:3.7 3:1.5 4:0.2
0 1:5.0 2:3.3 3:1.4 4:0.2
1 1:7.0 2:3.2 3:4.7 4:1.4
1 1:6.4 2:3.2 3:4.5 4:1.5
1 1:6.9 2:3.1 3:4.9 4:1.5
1 1:5.5 2:2.3 3:4.0 4:1.3
1 1:6.5 2:2.8 3:4.6 4:1.5
1 1:5.7 2:2.8 3:4.5 4:1.3
1 1:6.3 2:3.3 3:4.7 4:1.6
1 1:4.9 2:2.4 3:3.3 4:1.0
1 1:6.6 2:2.9 3:4.6 4:1.3
1 1:5.2 2:2.7 3:3.9 4:1.4
1 1:5.0 2:2.0 3:3.5 4:1.0
1 1:5.9 2:3.0 3:4.2 4:1.5
1 1:6.0 2:2.2 3:4.0 4:1.0
1 1:6.1 2:2.9 3:4.7 4:1.4
1 1:5.6 2:2.9 3:3.6 4:1.3
1 1:6.7 2:3.1 3:4.4 4:1.4
1 1:5.6 2:3.0 3:4.5 4:1.5
1 1:5.8 2:2.7 3:4.1 4:1.0
1 1:6.2 2:2.2 3:4.5 4:1.5
1 1:5.6 2:2.5 3:3.9 4:1.1
1 1:5.9 2:3.2 3:4.8 4:1.8
1 1:6.1 2:2.8 3:4.0 4:1.3
1 1:6.3 2:2.5 3:4.9 4:1.5
1 1:6.1 2:2.8 3:4.7 4:1.2
1 1:6.4 2:2.9 3:4.3 4:1.3
1 1:6.6 2:3.0 3:4.4 4:1.4
1 1:6.8 2:2.8 3:4.8 4:1.4
1 1:6.7 2:3.0 3:5.0 4:1.7
1 1:6.0 2:2.9 3:4.5 4:1.5
1 1:5.7 2:2.6 3:3.5 4:1.0
1 1:5.5 2:2.4 3:3.8 4:1.1
1 1:5.5 2:2.4 3:3.7 4:1.0
1 1:5.8 2:2.7 3:3.9 4:1.2
1 1:6.0 2:2.7 3:5.1 4:1.6
1 1:5.4 2:3.0 3:4.5 4:1.5
1 1:6.0 2:3.4 3:4.5 4:1.6
1 1:6.7 2:3.1 3:4.7 4:1.5
1 1:6.3 2:2.3 3:4.4 4:1.3
1 1:5.6 2:3.0 3:4.1 4:1.3
1 1:5.5 2:2.5 3:4.0 4:1.3
1 1:5.5 2:2.6 3:4.4 4:1.2
1 1:6.1 2:3.0 3:4.6 4:1.4
1 1:5.8 2:2.6 3:4.0 4:1.2
1 1:5.0 2:2.3 3:3.3 4:1.0
1 1:5.6 2:2.7 3:4.2 4:1.3
1 1:5.7 2:3.0 3:4.2 4:1.2
1 1:5.7 2:2.9 3:4.2 4:1.3
1 1:6.2 2:2.9 3:4.3 4:1.3
1 1:5.1 2:2.5 3:3.0 4:1.1
1 1:5.7 2:2.8 3:4.1 4:1.3

　　特征选择

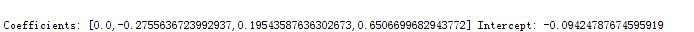
第一个特征权重为0，可以忽略，选择2，3，4个特征