fdtd二维

Posted 2020-09-20 I know you

先列出理论 

对于二维物质，在z向上是无变化的，可以有如下结论

1.假设激励源在z向也无变换，因此所有关于z的偏导都为0

2.再假设无自由电流和电荷

上面可以出现这样两个循环

\\(E_z \\Longrightarrow H_x  H_y\\Longrightarrow  E_z \\)   TM

\\(H_z \\Longrightarrow E_x  E_y \\Longrightarrow  H_z \\)   TE

 第二个循环对应的方程如下：

 \\(\\frac{\\partial E_x}{\\partial t}=\\frac{1}{\\epsilon}\\frac{\\partial H_z}{ \\partial y}\\) 

 \\(\\frac{\\partial E_y}{\\partial t}=-\\frac{1}{\\epsilon}\\frac{\\partial H_z}{ \\partial x}\\)

\\(\\frac{\\partial H_z}{\\partial t}=\\frac{1}{\\mu}\\left(\\frac{\\partial E_x}{ \\partial y}-\\frac{\\partial E_y}{ \\partial x}\\right)\\)

差分过程可以用下图来说明，O代表H_z，×代表E,两个H可以得到一个E，而反过来四个E又可以得到一个H，如此循环不断前进

 

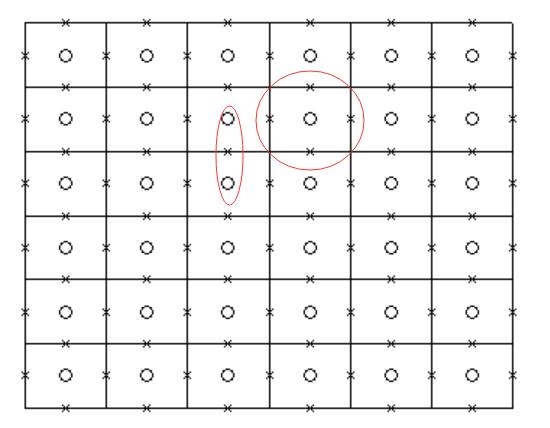
该图代码

 

figure();
hold on;
d=20
N=6;
for i=0:N
    plot([i*d,i*d],[0,N*d],\'-k\'); hold on;
    plot([0,N*d],[i*d,i*d],\'-k\'); hold on;
    plot(ones(N)*i*d,((1:N)-1/2)*d,\'kx\'); hold on;
    plot(((1:N)-1/2)*d,ones(N)*i*d,\'kx\'); hold on;
end
for i=1:N
    plot(((1:N)-1/2)*d,ones(N)*(i-1/2)*d,\'ko\'); hold on;
end
axis([-20,140,-20,140]);

 

根据以上关系，可以编写以上步进代码

 

N=201; %box number
pos_center=floor(N/2)+1;
N_cycle=400;
c_const=3e8;
mu=4*pi*1e-7;
epsilon=8.85*10^-12;
w=1e10;
dx=2*pi*c_const/w/10;
dy=dx;
dt=dx/c_const/2;
 
 %the edge is fixed to 0;
Ex=zeros(N+1,N);%box(i,j) upper
Ey=zeros(N,N+1);%box(i,j) left
Hz=zeros(N,N);%box(i,j) center
 
for i=1:N_cycle      
       %from Hz to Ex Ey
       Ex(2:N,1:N)=Ex(2:N,1:N)+dt/epsilon*(Hz(2:N,1:N)-Hz(1:N-1,1:N))/dy;
       Ey(1:N,2:N)= Ey(1:N,2:N)-dt/epsilon*(Hz(1:N,2:N)-Hz(1:N,1:N-1))/dx;
       %from Ex Ey to Hz
       Hz(1:N,1:N)=Hz(1:N,1:N)+dt/mu*( (Ex(2:N+1,1:N)-Ex(1:N,1:N))/dy ...
                                   -(Ey(1:N,2:N+1)-Ey(1:N,1:N))/dx);
        %add a cos source in the center                      
       Hz(pos_center,pos_center)=cos(w*i*dt);
        imshow(imresize(Hz/max(max(Hz)),10));
end

 

　　

 

附录：关于网格大小：要远小于波长（取0.1 lambda），且远小于物体尺寸