素数线性筛优化

Posted 2020-09-20 Fresh__air

大致思路：

　　初始时，令2是素数，假设2之后奇数全部数都是素数(偶数不考虑会快一点点)，从3开始每当找到一个素数时，显然这个素数乘上另外一个数之后都是合数，把这些合数都筛掉，直到最后一个奇数超出范围，剩下的都是奇数都是素数。

　　注：以下代码只为得到n以内的素数，所以执行后标记数组中的标记是不完整的，如函数1和2中的isPrime[4]=1显然是错的，不过这对prime数组没有影响。如果想使标记数组完整，请自行修改。

前提：

1 #include<bits/stdc++.h>
2 using namespace std;
3 
4 const int MN=1e+8;
5 bool isPrime[MN];//isPrime[i]:i是否素数 
6 int prime[MN/10];//prime[i]:第i个素数 

1.普通筛法：

 1 int makePrime1(int n)//求n以内的素数，返回得到的素数个数，下同 
 2 {
 3     memset(isPrime,1,sizeof(isPrime));
 4     memset(prime,0,sizeof(prime));
 5     //
 6     prime[1]=2;
 7     int cnt=1;
 8     for(long long i=3;i<=n;i+=2)
 9     {
10         if(isPrime[i])
11         {
12             prime[++cnt]=i;
13             for(long long j=i*i;j<=n;j+=i)//1此处初始值 j=i*i 比 j=i+i 要快;i和j用long long，因为i*i可能超出int范围
14                 isPrime[j]=0;
15         }
16     }
17     return cnt;
18 }

2.线性筛法：每个合数只筛一次

 1 int makePrime2(int n)
 2 {
 3     memset(isPrime,1,sizeof(isPrime));
 4     memset(prime,0,sizeof(prime));
 5     //
 6     prime[1]=2;
 7     int cnt=1;
 8     for(int i=3;i<=n;i+=2)
 9     {
10         if(isPrime[i])
11             prime[++cnt]=i;
12         for(int j=1;j<=cnt&&i*prime[j]<=n;j++)//关键 
13         {
14              isPrime[i*prime[j]]=0;
15              if(!(i%prime[j])) //(1)
16                  break;
17         }
18     }
19     return cnt;
20 }

　　关键for循环的作用：

　　　　1）i是素数：标记 i*prime[j]（prime[j]为比i小的素数）为合数。

　　　　2）i是合数：标记 i*prime[j]（prime[j]为比 i 的最小素数因子更小或相等的素数）为合数，因为当prime[j]从2增加到 i 的最小素数因子（即（1）成立）时接下来就break了。

 

3.线性筛法空间优化（1）：用每个bool/char isPrime[i]的每一位表示一个数（0，1，2......）的标记；

　　　　　　　　　　　　  则从0到n数 i 在数组中的标记为 isPrime[i/8]&(1<<(i%8))。逻辑同上，只需改3处，可节省大量空间

 1 int makePrime3(int n)
 2 {
 3     memset(isPrime,-1,sizeof(isPrime)); //(1)把每一位变成1 
 4     memset(prime,0,sizeof(prime));
 5     //
 6     prime[1]=2;
 7     int cnt=1;
 8     for(int i=3;i<=n;i+=2)
 9     {
10         if(isPrime[i/8]&(1<<(i%8))) //(2)判断i是否为素数
11             prime[++cnt]=i;
12         for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
13         {
14             int t=i*prime[j];
15             isPrime[t/8]&=(~(1<<(t%8))); //(3)把isPrime[t/8]的第t%8位变为0
16             if(!(i%prime[j]))
17                  break;
18         }
19     }
20     return cnt;
21 }

4.线性筛法空间优化（2）：bool/char isPriem[i]中的每一位只存奇数（1,3,5,7......i，对应序号为0,1,2,3.......(i-1)/2）的标记，可使isPrime数组再节省一半空间；

　　　　　　　　　　　　  则从1到n奇数 i 在数组中的标记为isPrime[(i-1)/2/8]&(1<<((i-1)/2%8))。

 1 int makePrime4(int n)
 2 {
 3     memset(isPrime,-1,sizeof(isPrime)); 
 4     memset(prime,0,sizeof(prime));
 5     //
 6     prime[1]=2;
 7     int cnt=1;
 8     for(int i=3;i<=n;i+=2)
 9     {
10         if(isPrime[(i-1)/2/8]&(1<<((i-1)/2%8))) //(1)将i改为(i-1)/2即可 
11             prime[++cnt]=i;
12         for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
13         {
14             int t=i*prime[j];
15             if(t%2)    //(2)当t为奇数时才有标记可以改变，偶数直接忽略 
16                 isPrime[(t-1)/2/8]&=(~(1<<((t-1)/2%8))); //t改成(t-1)/2即可
17             if(!(i%prime[j]))
18                  break;
19         }
20     }
21     return cnt;
22 }

 注：空间优化通常会增加时间负担

附下4个函数求五千万以内的素数的运行时间：

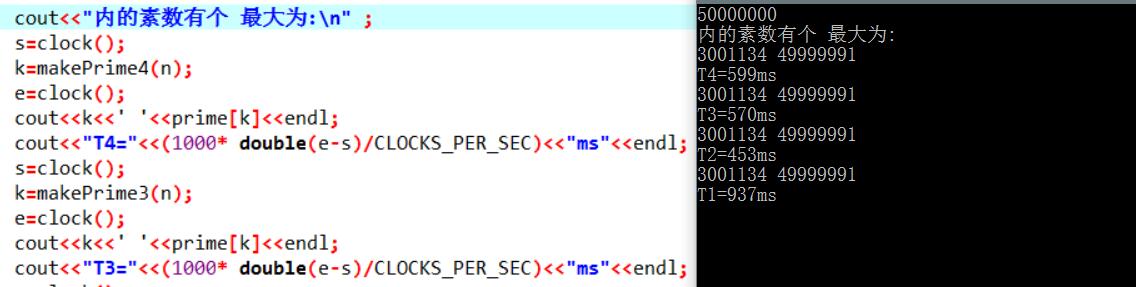
测评代码：

 1 int main()
 2 {
 3     clock_t s,e;
 4     int n,k;
 5     while(cin>>n)
 6     {
 7         cout<<"内的素数有个 最大为:\\n" ;
 8         s=clock();
 9         k=makePrime4(n);
10         e=clock();
11         cout<<k<<\' \'<<prime[k]<<endl;
12         cout<<"T4="<<(1000* double(e-s)/CLOCKS_PER_SEC)<<"ms"<<endl;
13         s=clock();
14         k=makePrime3(n);
15         e=clock();
16         cout<<k<<\' \'<<prime[k]<<endl;
17         cout<<"T3="<<(1000* double(e-s)/CLOCKS_PER_SEC)<<"ms"<<endl;
18         s=clock();
19         k=makePrime2(n);
20         e=clock();
21         cout<<k<<\' \'<<prime[k]<<endl;
22         cout<<"T2="<<(1000* double(e-s)/CLOCKS_PER_SEC)<<"ms"<<endl;
23         s=clock();
24         k=makePrime1(n);
25         e=clock();
26         cout<<k<<\' \'<<prime[k]<<endl;
27         cout<<"T1="<<(1000* double(e-s)/CLOCKS_PER_SEC)<<"ms"<<endl;
28         
29     }
30     return 0;
31 }