双因素方差检验

Posted 2020-09-20

 

 

数据来源

https://github.com/thomas-haslwanter/statsintro_python/tree/master/ISP/Code_Quantlets/08_TestsMeanValues/anovaTwoway

 

 

 

 

# -*- coding: utf-8 -*-
"""
Created on Tue May 30 10:16:54 2017

@author: daxiong
"""

# Import standard packages
import numpy as np
import pandas as pd

# additional packages
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

# Get the data
inFile = ‘altman_12_6.txt‘
data = np.genfromtxt(inFile, delimiter=‘,‘)

def anova_interaction(data):
    ‘‘‘ANOVA with interaction: Measurement of fetal head circumference,
    by four observers in three fetuses, from a study investigating the
    reproducibility of ultrasonic fetal head circumference data.
    ‘‘‘
    
    
    
    # Bring them in DataFrame-format
    df = pd.DataFrame(data, columns=[‘hs‘, ‘fetus‘, ‘observer‘])
    
    # Determine the ANOVA with interaction
    #C(fetus):C(observer)表示两者的交互
    formula = ‘hs ~ C(fetus) + C(observer) + C(fetus):C(observer)‘
    lm = ols(formula, df).fit()
    anovaResults = anova_lm(lm)
    # --- >>> STOP stats <<< ---
    print(anovaResults)

    return  anovaResults[‘F‘][0]
                              
anova_interaction(data)
‘‘‘
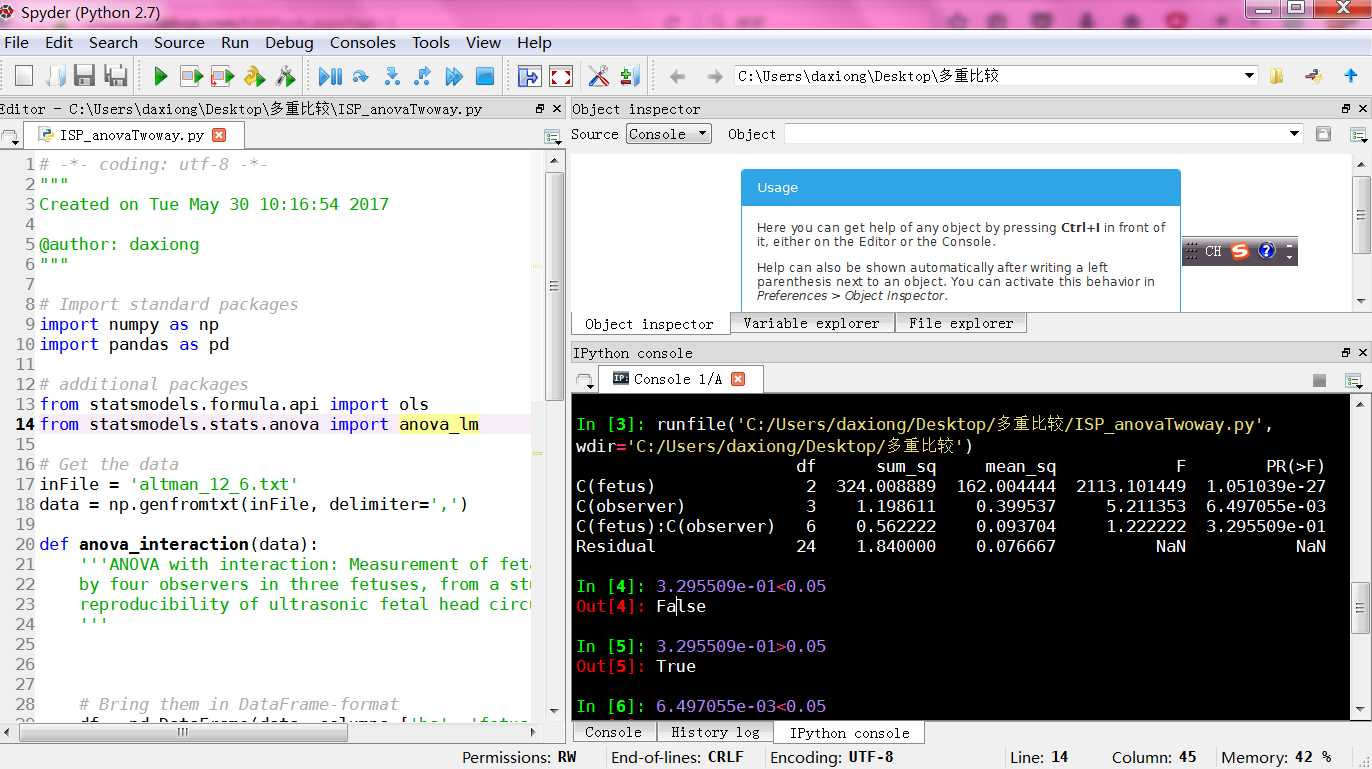
                      df      sum_sq     mean_sq            F        PR(>F)
C(fetus)               2  324.008889  162.004444  2113.101449  1.051039e-27
C(observer)            3    1.198611    0.399537     5.211353  6.497055e-03
C(fetus):C(observer)   6    0.562222    0.093704     1.222222  3.295509e-01
Residual              24    1.840000    0.076667          NaN           NaN

fetus和observer的交互没有显著影响
3.295509e-01>0.05
Out[5]: True

6.497055e-03<0.05
Out[6]: True

‘‘‘