20170529_3 数论_gcd 题解

Posted 2020-09-20

1.LCM Range最小公倍数

其实就是求 l 到 r 这么多自然数的最小公倍数。

需要注意LCM的求法，

理论：a与b的最小公倍数＝a*b/gcd(a,b)。

这里，lcm=ans*i*gcd(ans,i)

在后面的学习中由于ans*i可能很大，容易爆

所以可以写作：lcm=ans*gcd(ans,i)*i （交换律）

最终的答案由于就是当前答案和后一个数的lcm

代码如下：

var l,r,i,ans:longint;
function gcd(x,y:qword):qword;
begin
 if y=0 then gcd:=x
 else gcd:=gcd(y,x mod y);
end;
begin
assign(input,‘lcm.in‘);
assign(output,‘lcm.out‘);
reset(input);
rewrite(output);
 readln(l,r);
 ans:=1;
 for i:=l to r do
   ans:=ans div gcd(ans,i)*i ;//迭代
 writeln(ans);
close(input);
close(output);
end.

2.最大公约数(gcd.pas/c/cpp)

下面要解析的是一道 NOI 2012 chess 的原题！orz

请首先看：对于 100%：N, Q <= 100000，所有数的绝对值始终小于等于 10^16

这是数据范围，吓蒙了！果然是NOI难度啊（其实这种难度好像算NOI历史最低了吧？）

模拟就不用说了吧，太简单！于是就来对于100%数据的题解。

这里用到gcd的求法2：

更相减损法

“关于约分问题,实质是如何求分子,分母最大公约数的问题.<九章算术>中介绍了这个方法,叫做”更相减损术”,即“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”

翻译成现代语言如下：
　　第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
　　第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
　　则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
　　其中所说的“等数”，就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法。

数学家刘徽对此法进行了明确的注解和说明,是一个实用的数学方法,中学生应该掌握它.

如何证明?不妨举个栗子：

今有九十一分之四十九,问约之得几何?注：实质上就是求gcd

我们用(91,49)表示91和49的最大公约数.按刘徽所说,分别列出分子,分母,”以少减多,更相减损,求其等也,以等数约之,等数约之,即除也,其所以相减者皆等数之重叠,故以等数约之.”译文如下：约分的法则是：若分子、分母均为偶数时，可先被2除，否则，将分子与分母之数列在它处，然后以小数减大数，辗转相减，求它们的最大公约数，用最大公约数去约简分子与分母。其与古希腊欧几里德所著的《几何原本》中卷七第一个命题所论的相同。列式如下:

91≡42（mod49)

49≡7（mod42)

7│42

再来看一个栗子：

(24,15)->(9,15)->(9,6)->(3,6)->(3,3)

说明了：

每次所得两数与前两数有相同的等数,两数之值逐步减少,因而到有限步后必然获得相同的两数,也即所求的等数,其理由不证自明.

证明更相减损法成立！

用现代语言来说就是 (a, b) = (a, a - b)

接下来就是推论下去：

gcd(a[1], a[2]) = gcd(a[1], a[2] – a[1])
gcd(a[2], a[3]) = gcd(a[2], a[3] – a[2])
gcd(a[1], a[2], a[3]) = gcd(a[1], a[2]–a[1], a[3]–a[2])
………
gcd(a[1], … , a[n]) = gcd(a[1], a[2]–a[1],………,a[n]–a[n - 1])

对于题目中所说每个数都加增加了多少其实不需要使用O(n)的算法

这里可以看到：上面的式子中除了a[1]其他都是不变的！

即 d=a[2]–a[1],………,a[n]–a[n - 1]（d为常数）

于是原来O(n)的算法变成了O(1)累加a[1]即可！

在读入a[2..n]数据时就处理gcd，得到常数d，

对于1到Q就形成O(N) – O(1)  在线算法。

总结一下本题思路：怎么求gcd?

(a, b) = (b, a mod b)--->(a, b) = (a, a - b)

gcd(a[1], a[2]) = gcd(a[1], a[2] – a[1])
gcd(a[2], a[3]) = gcd(a[2], a[3] – a[2])
gcd(a[1], a[2], a[3]) = gcd(a[1], a[2]–a[1], a[3]–a[2])
………
gcd(a[1], … , a[n]) = gcd(a[1], a[2]–a[1],………,a[n]–a[n - 1])
上面的式子中除了a[1]其他都是不变的！因此可事先预处理出来

即读入a[2..n]数据时就处理gcd，得到d，但需要考虑a[i]-a[i-1]可能为负数（简单的将其为abs(a[i]-a[i-1])）。
每次修改a[1],求gcd(a[1],d)即是答案。
O(N) – O(1) 在线算法

代码如下：

var n,q,i:longint;
    a:array[0..100000]of int64;
    d,t:int64;
function gcd(a,b:int64):int64;
begin
 if a<0 then a:=-a;
 if b<0 then b:=-b;
 if b=0 then exit(a)
   else exit(gcd(b,a mod b));
end;
begin
assign(input,‘gcd.in‘);
assign(output,‘gcd.out‘);
reset(input);
rewrite(output);
 readln(n,q);
 d:=0;
 for i:=1 to n do begin
  read(a[i]);
  if i<>1 then d:=gcd(a[i]-a[i-1],d);
 end;
 for i:=1 to q do begin
  read(t);
  a[1]:=a[1]+t;
  writeln(gcd(a[1],d));
 end;
 close(input);
 close(output);
end.

3.约数统计AHOI2005

安徽省队选拔的水题！但是还是orz

N=4时：

1：1

2：1、2

3：1、3

4：1、2、4

我们可以发现 总和中1出现了n次，2出现了n/2次，3出现了n/3次……答案就是n+n/2+n/3+n/4（这里的/其实是div）

于是推广一下：

考虑[1,n]中每个数的约数当中有i的数就是n div i个。因此i对答案的贡献就是n div i。

∴ans=（n+n/2+n/3+……+n/n ）mod (10^9+7)（这里的/其实是div）

程序如下：

var n,i,sum,p:longint;
begin
assign(input,‘1.in‘);
assign(output,‘1.out‘);
reset(input);
rewrite(output);
 p:=1000000007;
 readln(n);
 for i:=1 to n do
  sum:=(sum+n div i)mod p;
 writeln(sum mod p);
close(input);
close(output);
end.

4.最轻的天平 (mobile.c/cpp/pas)L1961

https://www.luogu.org/problem/show?pid=1961

有没有发现其实这个天平有点像完全二叉树?我也觉得像。

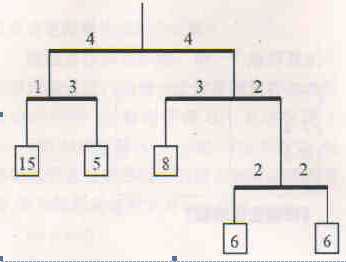
解决这道题需要3个分析知识：

●题目中的隐含条件为挂的物品必须为整数，即每个天平悬挂的物品重量必须为整数。（没什么好解释）
●题目的约束条件即为天平必须平衡，即重量与长度的乘积必须相等。（简单机械中的杠杆原理）
●左右没有天平(叶)的天平左右的单位重量都为1，该杠杆的最轻重量即为（p+q） div gcd(p,q) （转化一下就是 p div gcd(p,q) + q div gcd(p,q)）

总体的算法思想是：

若天平i左边的最轻重量为x，右边为y，则左边重量为ax，右边为by
∴ax*p=by*q，a:b=qy:xp，我们使a:b最简即可(求gcd)，ax+by即为天平的最轻重量。

(a,b∈N*) 是指a,b均为自然数

但是我们都不知道根节点是哪个怎么求呢？

这里用到类似并查集的算法：

 for i:=1 to n do begin
  readln(p[i],q[i],r[i],b[i]);
  fa[r[i]]:=true;
  fa[b[i]]:=true;
 end;
 for i:=1 to n do  if fa[i]=false then root:=i;

这样我们就找到了根root。

随后就是递归建树（假假的树）：

procedure build(k:longint; var ans:int64);
var t,d1,d2:int64;
begin
 if r[k]<>0 then build(r[k],d1) else d1:=1;//如果不是叶结点就递归深入，否则假定根节点是1开始累加退回
 if b[k]<>0 then build(b[k],d2) else d2:=1;//同上
 t:=(p[k]*d1)*(q[k]*d2) div gcd(p[k]*d1,q[k]*d2);//上面解释里a:b最简的值，即该结点（天平）的最小重量
 ans:=t div p[k]+ t div q[k];//预备知识3：该杠杆的最轻重量即为（p+q） div gcd(p,q) （转化一下就是 p div gcd(p,q) + q div gcd(p,q)）
end;

于是就做好了！

代码如下：

var i,root,n:longint;
    sum:int64;
    fa:array[0..1000]of boolean;
    p,q,r,b:array[1..1000]of longint;
function gcd(a,b:longint):longint;
 begin
  if b=0 then gcd:=a
   else gcd:=gcd(b,a mod b);
end;
procedure build(k:longint; var ans:int64);
var t,d1,d2:int64;
begin
 if r[k]<>0 then build(r[k],d1) else d1:=1;
 if b[k]<>0 then build(b[k],d2) else d2:=1;
 t:=(p[k]*d1)*(q[k]*d2) div gcd(p[k]*d1,q[k]*d2);
 ans:=t div p[k]+ t div q[k];
end;
begin
 assign(input,‘mobile.in‘); reset(input);
 assign(output,‘mobile.out‘); rewrite(output);
 readln(n);
 for i:=1 to n do begin
  readln(p[i],q[i],r[i],b[i]);
  fa[r[i]]:=true;
  fa[b[i]]:=true;
 end;
 for i:=1 to n do
  if fa[i]=false then root:=i;
 build(root,sum);
 writeln(sum);
 close(input);close(output);
end.