POJ 2391 Ombrophobic Bovines（二分+拆点+最大流）

Posted 2020-09-20 谦谦君子，陌上其华

 

http://poj.org/problem?id=2391

题意：

给定一个无向图，点i处有Ai头牛，点i处的牛棚能容纳Bi头牛，求一个最短时间T，使得在T时间内所有的牛都能进到某一牛棚里去。

 

思路：

建立一个源点和汇点，源点和牛棚的初始牛量相连，汇点和牛棚容量相连。这样跑最大流，如果最后流量等于牛的总数时，就说明是可以的。

那么，怎么连边呢？
二分时间，根据时间来连边，所以首先我们先跑一遍floyd计算出两点距离。然后在该时间下，如果d【i】【j】，那么就添加边（i，i\'，INF），表面这段路是可以走的。

注意，这里是需要拆点的！！！

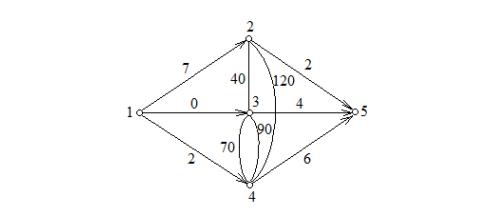
看这个建图，这个没有拆点，那么当我们的时间T=70的时候，只有（2,3）和（3,4）是满足的，但是在图中2-4也相连了，也就是说2-4也可以走，但事实上（2,4）这条路超过了时间设定。所以，不拆点是行不通的。

事实上，这个并不是一个二分图，任意点之间都可能有路径，所以需要拆点。

最后，注意这道题目的数据是很大的！！！

附上数据：http://contest.usaco.org/MAR05_4.htm

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<cstring>
  4 #include<cstdio>
  5 #include<vector>
  6 #include<stack>
  7 #include<queue>
  8 #include<cmath>
  9 #include<map>
 10 using namespace std;
 11 typedef long long LL;
 12 typedef pair<int,int> pll;
 13 const LL INF=1e16;
 14 const int maxn=500+5;
 15 
 16 int n,m;
 17 int full_flow;
 18 int s[maxn],t[maxn];
 19 LL g[maxn][maxn];
 20 
 21 struct Edge
 22 {
 23     int from,to,cap,flow;
 24     Edge(int u,int v,int w,int f):from(u),to(v),cap(w),flow(f){}
 25 };
 26 
 27 struct Dinic
 28 {
 29     int n,m,s,t;
 30     vector<Edge> edges;
 31     vector<int> G[maxn];
 32     bool vis[maxn];
 33     int cur[maxn];
 34     int d[maxn];
 35 
 36     void init(int n)
 37     {
 38         this->n=n;
 39         for(int i=0;i<n;++i) G[i].clear();
 40         edges.clear();
 41     }
 42 
 43     void AddEdge(int from,int to,int cap)
 44     {
 45         edges.push_back( Edge(from,to,cap,0) );
 46         edges.push_back( Edge(to,from,0,0) );
 47         m=edges.size();
 48         G[from].push_back(m-2);
 49         G[to].push_back(m-1);
 50     }
 51 
 52     bool BFS()
 53     {
 54         queue<int> Q;
 55         memset(vis,0,sizeof(vis));
 56         vis[s]=true;
 57         d[s]=0;
 58         Q.push(s);
 59         while(!Q.empty())
 60         {
 61             int x=Q.front(); Q.pop();
 62             for(int i=0;i<G[x].size();++i)
 63             {
 64                 Edge& e=edges[G[x][i]];
 65                 if(!vis[e.to] && e.cap>e.flow)
 66                 {
 67                     vis[e.to]=true;
 68                     d[e.to]=d[x]+1;
 69                     Q.push(e.to);
 70                 }
 71             }
 72         }
 73         return vis[t];
 74     }
 75 
 76     int DFS(int x,int a)
 77     {
 78         if(x==t || a==0) return a;
 79         int flow=0, f;
 80         for(int &i=cur[x];i<G[x].size();++i)
 81         {
 82             Edge &e=edges[G[x][i]];
 83             if(d[e.to]==d[x]+1 && (f=DFS(e.to,min(a,e.cap-e.flow) ) )>0)
 84             {
 85                 e.flow +=f;
 86                 edges[G[x][i]^1].flow -=f;
 87                 flow +=f;
 88                 a -=f;
 89                 if(a==0) break;
 90             }
 91         }
 92         return flow;
 93     }
 94 
 95     int Maxflow(int s,int t)
 96     {
 97         this->s=s; this->t=t;
 98         int flow=0;
 99         while(BFS())
100         {
101             memset(cur,0,sizeof(cur));
102             flow +=DFS(s,0x3f3f3f3f);
103         }
104         return flow;
105     }
106 }DC;
107 
108 void floyd()
109 {
110     for (int k = 1; k <= n; k++)
111     for (int i = 1; i <= n; i++)
112     for (int j = 1; j <= n; j++)
113         g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
114 }
115 
116 void init(LL x)
117 {
118     DC.init(2*n+2);
119 
120     for(int i=1;i<=n;i++)
121     {
122         DC.AddEdge(0,i,s[i]);
123         DC.AddEdge(i+n,2*n+1,t[i]);
124         DC.AddEdge(i,i+n,0x3f3f3f3f);
125     }
126 
127     for(int i=1;i<=n;i++)
128         for(int j=i+1;j<=n;j++)
129         if(g[i][j]<=x)
130     {
131         DC.AddEdge(i,j+n,0x3f3f3f3f);
132         DC.AddEdge(j,i+n,0x3f3f3f3f);
133     }
134 }
135 
136 int main()
137 {
138     //freopen("D:\\\\input.txt","r",stdin);
139     while(scanf("%d%d",&n,&m)!=EOF)
140     {
141         full_flow=0;
142         for(int i=1;i<=n;i++)
143         {
144             scanf("%d%d",&s[i],&t[i]);
145             full_flow+=s[i];
146         }
147 
148         for(int i=1;i<=n;i++)
149         {
150             for(int j=1;j<=n;j++)
151             g[i][j]=INF;
152             g[i][i]=0;
153         }
154 
155         for(int i=0;i<m;i++)
156         {
157             int u,v;
158             LL w;
159             scanf("%d%d%lld",&u,&v,&w);
160             if(w<g[u][v])  g[u][v]=g[v][u]=w;
161         }
162 
163         floyd();
164 
165         LL L=0,R=0;
166         LL ans=-1;
167 
168         for(int i=1;i<=n;i++)
169             for(int j=1;j<=n;j++)
170             if(g[i][j]!=INF)   R=max(R,g[i][j]);
171 
172         while(L<=R)
173         {
174             LL mid=(L+R)/2;
175             init(mid);
176             if(DC.Maxflow(0,2*n+1)==full_flow)
177             {
178                 ans=mid;
179                 R=mid-1;
180             }
181             else L=mid+1;
182         }
183         printf("%I64d\\n",ans);
184     }
185 
186     return 0;
187 }