Manacher算法—最长回文串

Posted 2020-09-20 启动

若字符串长度为n，则算法的时间复杂度为o(n)

假设有一个字符串abaaba

先把该字符串变成$  #  a  #  b  #  a  #  a  #  b  #  a  #

第一个字符设为‘$’，防止计算的时候数组越界

再计算p数组，先给出p数组的答案

i为坐标，ma数组放改变后的字符串，p数组代表以该字符为中心，向右和向左延伸p[i]个，是回文串

i      　0  1  2  3  4  5  6  7  8  9  10 11 12 13
ma[]   $  #  a  #  b  #  a   #  a  #  b   #   a   #
p[]      1  1  2  1  4  1  2   7  2  1   4  1   2   1

附上完整代码

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 typedef long long LL;
 6 const int maxn = 110000;
 7 char ma[maxn*2];
 8 int p[maxn*2];
 9 
10 void Manacher(char *s,int len) {
11     int l = 0;
12     ma[l++] = \'$\';
13     ma[l++] = \'#\';
14     for(int i = 0; i < len; i++) {
15         ma[l++] = s[i];
16         ma[l++] = \'#\';
17     }
18     ma[l] = 0;
19     int mx = 0,id = 0;
20     for(int i = 0; i < l; i++) {
21         p[i] = mx > i?min(p[2*id - i],mx - i) : 1;//这一步最为关键
22         while(ma[i + p[i]] == ma[i - p[i]]) p[i]++;
23         if(i+p[i] > mx) {
24             mx = i + p[i];//mx代表i位置向右延伸最右端的位置
25             id = i;//id记录最优mx情况下i的位置
26         }
27     }
28 }
29 int main() {
30     //freopen("in.txt","r",stdin);
31     //freopen("out.txt,"w",stdout");
32     ios_base::sync_with_stdio(0);cin.tie();
33      char s[110000];
34      while(scanf("%s",s) != EOF) {
35          int len = strlen(s);
36          Manacher(s, len);
37          int ans = 0;
38          for(int i = 0; i < 2*len+2; i++)
39              ans = max(ans, p[i] - 1);
40          printf("%d\\n",ans); 
41      }
42      return 0;
43 }
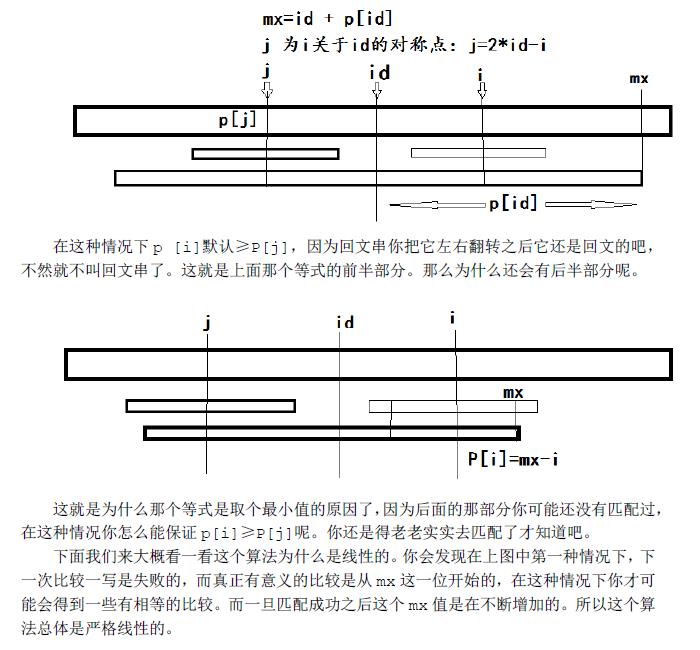
下列这图是盗用别人的，这张图很好诠释了p[i] = mx > i ? min(p[2*id - i],mx - i) : 1;

j = 2*id - 1; p[j] 已经算出来了，又因为id向左向右延伸mx都是回文的，所以p[i] == p[j] (在满足小于 mx - i 的情况下)