[2016-03-11][POJ][1609][Tiling Up Blocks]

Posted 2020-06-21 红洋

[2016-03-11][POJ][1609][Tiling Up Blocks]

Tiling Up Blocks

Time Limit: 1000MS

Memory Limit: 10000KB

64bit IO Format: %I64d & %I64u

Submit Status

Description

Michael The Kid receives an interesting game set from his grandparent as his birthday gift. Inside the game set box, there are n tiling blocks and each block has a form as follows: 

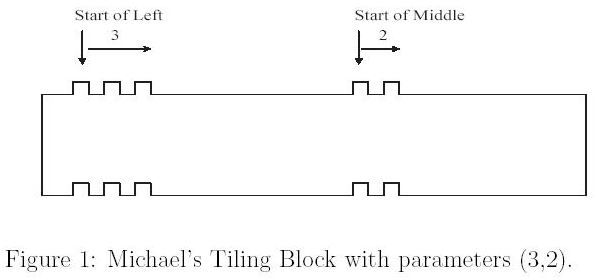
Each tiling block is associated with two parameters (l,m), meaning that the upper face of the block is packed with l protruding knobs on the left and m protruding knobs on the middle. Correspondingly, the bottom face of an (l,m)-block is carved with l caving dens on the left and m dens on the middle. 
It is easily seen that an (l,m)-block can be tiled upon another (l,m)-block. However,this is not the only way for us to tile up the blocks. Actually, an (l,m)-block can be tiled upon another (l‘,m‘)-block if and only if l >= l‘ and m >= m‘. 
Now the puzzle that Michael wants to solve is to decide what is the tallest tiling blocks he can make out of the given n blocks within his game box. In other words, you are given a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). The objective of the problem is to decide the number of tallest tiling blocks made from B. 

Input

Several sets of tiling blocks. The inputs are just a list of integers.For each set of tiling blocks, the first integer n represents the number of blocks within the game box. Following n, there will be n lines specifying parameters of blocks in B; each line contains exactly two integers, representing left and middle parameters of the i-th block, namely, li and mi. In other words, a game box is just a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). 
Note that n can be as large as 10000 and li and mi are in the range from 1 to 100. 
An integer n = 0 (zero) signifies the end of input.

Output

For each set of tiling blocks B, output the number of the tallest tiling blocks can be made out of B. Output a single star ‘*‘ to signify the end of 
outputs.

Sample Input

3
3 2
1 1
2 3
5
4 2
2 4
3 3
1 1
5 5
0

Sample Output

2
3
*

• 时间:2016-03-11 19:11:31 星期五
  
• 题目编号:POJ 1609 Tiling Up Blocks
  
• 题目大意:给定一个积木,每个积木有参数(l,m)当且仅当一个积木的 l‘ <= l && m‘ <= m 时这个积木可以堆到(l,m)的积木上,给定一堆积木,问对多能堆多高
  
• 输入:
  
• 多组数据
• 每组数据
• n积木的数目
• 接下来n行,每行两个数字,每个积木的参数
• n==0表示结束
• 输出:
  
• 每组数据输出一行,每行一个数字表示最大的高度
• 输入结束之后 输出 单独一行 * 表示结束
• 分析:
• 首先按l对积木排序,那么剩下的就是求最多能叠多高,这时候只需要对另外一个参数求最长非减子序列即可
• 解题过程遇到问题:
  
• dp忘记初始化

#include <vector> #include <list> #include <map> #include <set> #include <deque> #include <queue> #include <stack> #include <bitset> #include <algorithm> #include <functional> #include <numeric> #include <utility> #include <sstream> #include <iostream> #include <iomanip> #include <cstdio> #include <cmath> #include <cstdlib> #include <cctype> #include <string> #include <cstring> #include <cstdio> #include <cmath> #include <cstdlib> #include <ctime> using namespace std; typedef long long LL; #define CLR(x,y) memset((x),(y),sizeof((x))) #define FOR(x,y,z) for(int (x)=(y);(x)<(z);++(x)) #define FORD(x,y,z) for(int (x)=(y);(x)>=(z);--(x)) #define FOR2(x,y,z) int (x);for((x)=(y);(x)<(z);++(x)) #define FORD2(x,y,z) int (x);for((x)=(y);(x)>=(z);--(x)) typedef pair<int,int> Point; #define x first #define y second const int maxn = 10000 + 10; int dp[maxn]; Point a[maxn]; int main(){         //freopen("in.txt","r",stdin);         //freopen("out.txt","w",stdout);         int n;         while(~scanf("%d",&n) && n){                 FOR(i,0,n){                         scanf("%d%d",&a[i].x ,&a[i].y);                 }                 memset(dp,0,sizeof(dp));                 sort(a,a+n);                 CLR(dp,0);                 FOR(i,0,n){                         dp[i] = 1;                         FOR(j,0,i){                                 if(a[i].y >= a[j].y){                                         dp[i] = max(dp[i],dp[j] + 1);                                 }                         }                 }                 int ans = 0;                 FOR(i,0,n){                         ans = max(ans,dp[i]);                 }                 printf("%d\n",ans);         }         puts("*");         return 0; }

来自为知笔记(Wiz)