bzoj 2301: [HAOI2011]Problem b mobius反演 RE

Posted 2020-09-19 stupid_one

http://www.lydsy.com/JudgeOnline/problem.php?id=2301

设f(i)为在区间[1, n]和区间[1, m]中，gcd(x, y) = i的个数。

设F(i)为在区间[1, n]和区间[1, m]中，gcd(x, y) % i == 0的个数，很简单的公式就是floor(n / i) * floor(m / i)

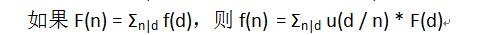
可知gcd(x, y) = k * i也属于F(i)的范围，所以可以反演得到f(i)的表达式。

算一次复杂度O（n），而且询问区间的时候要拆分成4个区间来容斥，所以总复杂度会达到4 * 5e4 * 5e4 = 1e10

 

技巧：（和省赛E题一样的技巧，无奈省赛一直卡E）

注意到，floor(n / i)的取值，很多是相同的，比如，7 / 2 = 7 / 3

7 / 4 = 7 / 5 = 7 / 6 = 7 / 7，注意到，值是n / i的，起点是i，终点是n / floor(n / i)

那么可以把相同的放在一起了，虽然是要两个相同才放一起，就是n / i和m / i，但是还是很好写的。

注意不要用cout，莫名re，re一小时

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define ios ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;


#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
#include <time.h>
const int maxn = 5e4 + 20;
int prime[maxn];//这个记得用int，他保存的是质数，可以不用开maxn那么大
bool check[maxn];
int total;
int mu[maxn];
void initprime() {
    mu[1] = 1; //固定的
    for (int i = 2; i <= maxn - 20; i++) {
        if (!check[i]) { //是质数了
            prime[++total] = i; //只能这样记录，因为后面要用
            mu[i] = -1; //质因数分解个数为奇数
        }
        for (int j = 1; j <= total; j++) { //质数或者合数都进行的
            if (i * prime[j] > maxn - 20) break;
            check[i * prime[j]] = 1;
            if (i % prime[j] == 0) {
                mu[prime[j] * i] = 0;
                break;
            }
//            if (prime[j] * i > maxn - 20) while(1);
            mu[prime[j] * i] = -mu[i];
            //关键，使得它只被最小的质数筛去。例如i等于6的时候。
            //当时的质数只有2,3,5。6和2结合筛去了12，就break了
            //18留下等9的时候，9*2=18筛去
        }
    }
}
int sumMu[maxn];
LL ask(int n, int m, int k) {
    if (k == 0) return 0;
    n /= k;
    m /= k;
    LL ans = 0;
    int mi = min(n, m);
    int nxt;
    for (int i = 1; i <= mi; i = nxt + 1) {
        nxt = min((n / (n / i)), (m / (m / i)));
        ans += (sumMu[nxt] - sumMu[i - 1]) * 1LL * (n / i) * (m / i);
    }
    return ans;
}
void work() {
    int a, b, c, d, k;
//    cin >> a >> b >> c >> d >> k;
    scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
    LL ans = ask(b, d, k) - ask(d, a - 1, k) - ask(c - 1, b, k) + ask(a - 1, c - 1, k);
    printf("%lld\\n", ans);
//    cout << ans << endl;
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    initprime();
    for (int i = 1; i <= maxn - 20; ++i) {
        sumMu[i] = sumMu[i - 1] + mu[i];
    }
    int t;
    scanf("%d", &t);
    while (t--) work();
    return 0;
}

View Code