机器学习笔记（Washington University）- Clustering Specialization-week one & week two

Posted 2020-09-19

,1.One nearest neighbor

Input:

　　Query article: X_q

　　Corpus of documents (N docs): (X₁, X₂, X₃,... ,X_N)

output :

　　X^NN = min disance(X_q, X_i)

 

2. K-NN Algorithm

#list of sorted distance
smallest_distances = sort(σ1, σ2...σk) 
#list of sorted distance
closest_articles = sort(book1,  book2...bookK)

For i=k+1,...,N
compute σ = distance(book1 ,bookq)
if σ < smallest_distances[k]:

 　 find j such that σ  > smallest_distances[j-1] but  σ  < smallest_distances[j]

　　remove furthest article and shift queue:

　　　　closest_articles[j+1:k] =  closest_articles[j:k-1]

　　　　smallest_distances [j+1:k] =  smallest_distances [j:k-1]

　　set smallest_distances[j] = σ and smallest_distances[j]  = booki

return k most similar articles

 

3. Document representation

i. Bag of words model

• Ignore order of words
• Count number of instances of each word in vocabulary

Issue：

• Common words in the doc like "the" dominate rare words llike "football"

 

ii. TF-IDF document representation

• emphasize important words which appear frequently in document  but rarely in corpus

And if defined as tf*idf :

(tf) Term frequency = word counts

(idf) Inverse doc frequency = log(number of docs/(1+number of docs which are using this word))

 

4. Distance metric

i.Weight different features:

• some features are relevant than others
• some features vary more than others

Specify weights as a function of feature spread

For feature j:

　　1 / (max(x_i[j]) - min(X_i[j]))

Scaled euclidean distance:

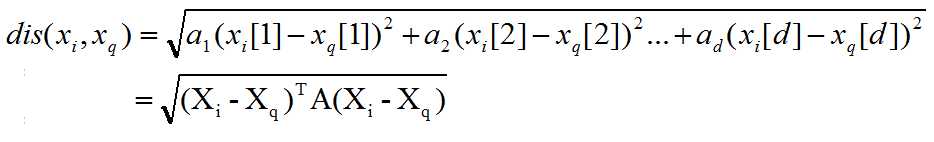
and A is the diagonal matrix where a1, a2, ..., ad is the diagonal

 

ii. Similarity

the inner product between two article vectors,

• it is not a proper  distance metric, distance = 1 - similarity
• efficient to compute for sparse vecs

Normalized similarity is defined as:

 

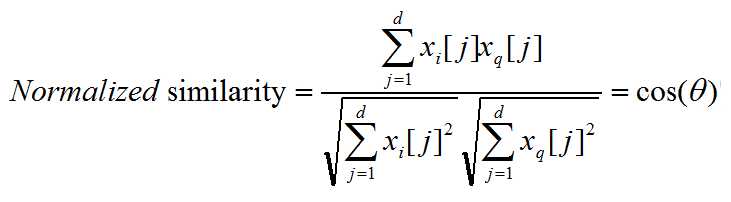
Theta is the angle between those two vector.

We can normalized the similarity to rule out the effect of the length of an article,

but normalizing can make dissimilar objects appear more similar like tweet vs long article, we can cap maximum word counts to cure this.

 

 5. Complexity of brute-force search of KNN

O(N) distance computations per 1-NN query

O(NlogK) per k-NN query (maintain a priority queue and insert into it in an efficient manner)

 

6. KD-trees

• Strucured organization of documents: recursively partitions points into axis aligned boxes
• enable more efficient pruning of search space
• works wll in low-medium dimensions

which dimensin do we split along?

• widest (or alternate)

which value do we split at?

• median or center point of box(ignoring data in box)

when do we stop?

• fewer than m points left or box hits minimum width

 

7. KNN with KD-trees

• start by exploring leaf node containing query poing
• compute distance to each other point at leaf node
• backtracke and try other branch at each node visited
• use distance bound and bounding box of each node to prune parts of tree that cannot include nearest neightbor (distance to bounding box > distance to nearest neighbor sofar)

Complexity of this algorithm

Construction:

　　size = 2N - 1 odes if 1 datapoint at each leaf  O(N）

　　depth = Olog(N)

　　median + send points left right = O(N) at every level of the tree

　　Construction time = depth * cost at each level = O(Nlog(N))

1-NN Query：

　　Traverse down tree to starting point = O(log(N))

　　Maximum backtrack and traverse = O(N) in worst case

　　Complexity range: O(log(N)) - O(N) but exponential in d (dimensions)

for k queries, original KNN method = O(N²) ,using KD trees = O(Nlog(N)) - O(N²)

In high dimensions:

• most dimensions are just noise, everything is far away. and the search radius is likely to intersect many hypercubes in at least on dim
• not many nodes can be pruned
• need technique to learn which features are important to given task

 

8. Approximate K-NN with KD-trees

Before: Prune when distance to bounding box > r

Now: Prune when distance to bounding box > r/α

so we can prune more  than allowed 

 

9. Locality sensitive hashing

simple "binning" of data into multiple bins, and we only search points within the bin, fewer points in the bin

 

• Draw h random lines
• Compute score for each point under each line and translate to binary index
• use h-bit binary vector per data point as bin index
• create hash table
• for each query point x, search bin(x) then searching neighboring bins

Each line can split points, so we are sacrificing accuray for speed.

but we can search neighboring bins(filp 1 bit, until computational budget is reached).

 

In high dimensions, we just draw random planes and per daa point, need d multiplies to determine bin index per plane.