求教用matlab 实现最小二乘法拟合曲线的问题

Posted 2023-04-30

数据如下：x=(1,2,3,4,5,6,7,8,9,10)
y=( 96.31, 135.44, 79.5, 56.54, 256.21, 350.68, 105.62, 185.03, 493.08, 1031.17, 860.06, 746.78)
表达式为：Y = a x4+b x3+c x2+d x+e
求：a,b,c,d,e,以及 可靠度 ，请高手赐教，怎么用matlab 实现，本人菜鸟，请说详细点
谢谢各位，但能不能详细说一下怎么确定拟合曲线的精确度？
另：修改x=(1,2,3,4,5,6,7,8,9,10，11，12) ，上面后两个数忘了加上了。

使用多项式拟合函数polyfit(x,y,n),其中x是你要你和的自变量，y是你要拟合的因变量，n是你要用到的拟合多项式的最高次数，函数返回这个多项式。
具体你的问题：
x=[1,2,3,4,5,6,7,8,9,10，11，12]
y=[ 96.31, 135.44, 79.5, 56.54, 256.21, 350.68, 105.62, 185.03, 493.08, 1031.17, 860.06, 746.78]
z=polyfit（x，y，4）
ans =

-0.9026 22.3624 -171.6814 489.5975 -287.8153 参考技术A y比x多出了两位，我删除了后两位；
代码如下：
function poly4(x,y)
%POLY4 Create plot of datasets and fits
% POLY4(X,Y)
% Creates a plot, similar to the plot in the main curve fitting
% window, using the data that you provide as input. You can
% apply this function to the same data you used with cftool
% or with different data. You may want to edit the function to
% customize the code and this help message.
%
% Number of datasets: 1
% Number of fits: 1

% Data from dataset "y vs. x":
% X = x:
% Y = y:
% Unweighted
%
% This function was automatically generated on 27-Mar-2009 21:43:52

% Set up figure to receive datasets and fits
f_ = clf;
figure(f_);
set(f_,'Units','Pixels','Position',[326 106 680 484]);
legh_ = []; legt_ = ; % handles and text for legend
xlim_ = [Inf -Inf]; % limits of x axis
ax_ = axes;
set(ax_,'Units','normalized','OuterPosition',[0 0 1 1]);
set(ax_,'Box','on');
axes(ax_); hold on;

% --- Plot data originally in dataset "y vs. x"
x = x(:);
y = y(:);
h_ = line(x,y,'Parent',ax_,'Color',[0.333333 0 0.666667],...
'LineStyle','none', 'LineWidth',1,...
'Marker','.', 'MarkerSize',12);
xlim_(1) = min(xlim_(1),min(x));
xlim_(2) = max(xlim_(2),max(x));
legh_(end+1) = h_;
legt_end+1 = 'y vs. x';

% Nudge axis limits beyond data limits
if all(isfinite(xlim_))
xlim_ = xlim_ + [-1 1] * 0.01 * diff(xlim_);
set(ax_,'XLim',xlim_)
else
set(ax_, 'XLim',[0.91000000000000003, 10.09]);
end

% --- Create fit "fit 1"
ok_ = isfinite(x) & isfinite(y);
if ~all( ok_ )
warning( 'GenerateMFile:IgnoringNansAndInfs', ...
'Ignoring NaNs and Infs in data' );
end
ft_ = fittype('poly4');

% Fit this model using new data
cf_ = fit(x(ok_),y(ok_),ft_);

% Or use coefficients from the original fit:
if 0
cv_ = 1.9494012237762368, -37.46559731934768, 242.74933129370976, -576.15945804197111, 496.91083333334984;
cf_ = cfit(ft_,cv_:);
end

% Plot this fit
h_ = plot(cf_,'fit',0.95);
legend off; % turn off legend from plot method call
set(h_(1),'Color',[1 0 0],...
'LineStyle','-', 'LineWidth',2,...
'Marker','none', 'MarkerSize',6);
legh_(end+1) = h_(1);
legt_end+1 = 'fit 1';

% Done plotting data and fits. Now finish up loose ends.
hold off;
leginfo_ = 'Orientation', 'vertical', 'Location', 'NorthEast';
h_ = legend(ax_,legh_,legt_,leginfo_:); % create legend
set(h_,'Interpreter','none');
xlabel(ax_,''); % remove x label
ylabel(ax_,''); % remove y label

结果：
Linear model Poly4:
f(x) = p1*x^4 + p2*x^3 + p3*x^2 + p4*x + p5
Coefficients (with 95% confidence bounds):
p1 = 1.949 (-0.1406, 4.039)
p2 = -37.47 (-83.7, 8.768)
p3 = 242.7 (-103.2, 588.7)
p4 = -576.2 (-1575, 422.8)
p5 = 496.9 (-389.4, 1383)

Goodness of fit:
SSE: 5.445e+004
R-square: 0.9319
Adjusted R-square: 0.8774
RMSE: 104.4 参考技术B 请使用多项式拟合函数polyfit(x,y,n),其中x是你要你和的自变量，y是你要拟合的因变量，n是你要用到的拟合多项式的最高次数，函数返回这个多项式。
详见MATLAB帮助文档：polyfit

最小二乘法多项式曲线拟合原理与实现（转）

概念

最小二乘法多项式曲线拟合，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。

 

原理

[原理部分由个人根据互联网上的资料进行总结，希望对大家能有用]

 

 

     给定数据点pi(xi,yi)，其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y，i=1,2,...,m。 

常见的曲线拟合方法:

     1.使偏差绝对值之和最小

     

 

     2.使偏差绝对值最大的最小

     

 

     3.使偏差平方和最小

 

     

 

     按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

推导过程：

     1. 设拟合多项式为：

          

     2. 各点到这条曲线的距离之和，即偏差平方和如下：

          

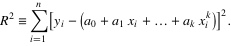
     3. 为了求得符合条件的a值，对等式右边求ai偏导数，因而我们得到了： 

          

          

                         .......

          

 

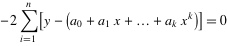
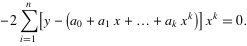
     4. 将等式左边进行一下化简，然后应该可以得到下面的等式：

          

          

                     .......

          

 

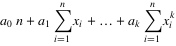
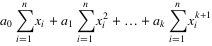
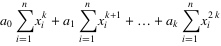
     5. 把这些等式表示成矩阵的形式，就可以得到下面的矩阵：

          

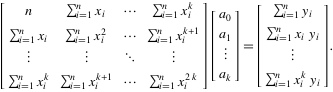
     6. 将这个范德蒙得矩阵化简后可得到:

          

     7. 也就是说X*A=Y，那么A = (X‘*X)-1*X‘*Y，便得到了系数矩阵A，同时，我们也就得到了拟合曲线。

实现

 

运行前提:

1. Python运行环境与编辑环境；
2. Matplotlib.pyplot图形库，可用于快速绘制2D图表，与matlab中的plot命令类似，而且用法也基本相同。

代码:

[python] view plain copy

 

1. # coding=utf-8  
2.   
3. ‘‘‘‘‘ 
4. 作者:Jairus Chan 
5. 程序:多项式曲线拟合算法 
6. ‘‘‘  
7. import matplotlib.pyplot as plt  
8. import math  
9. import numpy  
10. import random  
11.   
12. fig = plt.figure()  
13. ax = fig.add_subplot(111)  
14.   
15. #阶数为9阶  
16. order=9  
17.   
18. #生成曲线上的各个点  
19. x = numpy.arange(-1,1,0.02)  
20. y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x]  
21. #ax.plot(x,y,color=‘r‘,linestyle=‘-‘,marker=‘‘)  
22. #,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5"  
23.   
24. #生成的曲线上的各个点偏移一下，并放入到xa,ya中去  
25. i=0  
26. xa=[]  
27. ya=[]  
28. for xx in x:  
29.     yy=y[i]  
30.     d=float(random.randint(60,140))/100  
31.     #ax.plot([xx*d],[yy*d],color=‘m‘,linestyle=‘‘,marker=‘.‘)  
32.     i+=1  
33.     xa.append(xx*d)  
34.     ya.append(yy*d)  
35.   
36. ‘‘‘‘‘for i in range(0,5): 
37.     xx=float(random.randint(-100,100))/100 
38.     yy=float(random.randint(-60,60))/100 
39.     xa.append(xx) 
40.     ya.append(yy)‘‘‘  
41.   
42. ax.plot(xa,ya,color=‘m‘,linestyle=‘‘,marker=‘.‘)  
43.   
44.   
45. #进行曲线拟合  
46. matA=[]  
47. for i in range(0,order+1):  
48.     matA1=[]  
49.     for j in range(0,order+1):  
50.         tx=0.0  
51.         for k in range(0,len(xa)):  
52.             dx=1.0  
53.             for l in range(0,j+i):  
54.                 dx=dx*xa[k]  
55.             tx+=dx  
56.         matA1.append(tx)  
57.     matA.append(matA1)  
58.   
59. #print(len(xa))  
60. #print(matA[0][0])  
61. matA=numpy.array(matA)  
62.   
63. matB=[]  
64. for i in range(0,order+1):  
65.     ty=0.0  
66.     for k in range(0,len(xa)):  
67.         dy=1.0  
68.         for l in range(0,i):  
69.             dy=dy*xa[k]  
70.         ty+=ya[k]*dy  
71.     matB.append(ty)  
72.    
73. matB=numpy.array(matB)  
74.   
75. matAA=numpy.linalg.solve(matA,matB)  
76.   
77. #画出拟合后的曲线  
78. #print(matAA)  
79. xxa= numpy.arange(-1,1.06,0.01)  
80. yya=[]  
81. for i in range(0,len(xxa)):  
82.     yy=0.0  
83.     for j in range(0,order+1):  
84.         dy=1.0  
85.         for k in range(0,j):  
86.             dy*=xxa[i]  
87.         dy*=matAA[j]  
88.         yy+=dy  
89.     yya.append(yy)  
90. ax.plot(xxa,yya,color=‘g‘,linestyle=‘-‘,marker=‘‘)  
91.   
92. ax.legend()  
93. plt.show()  

运行效果: 

 

 

 

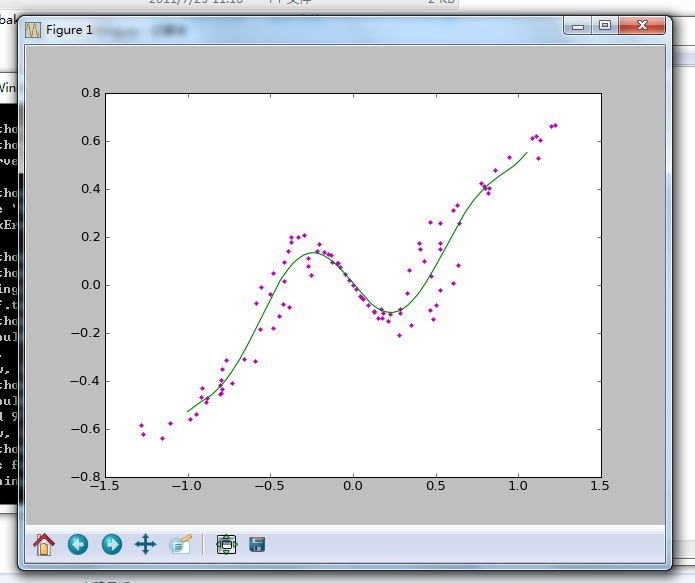
本博客中所有的博文都为笔者（Jairus Chan）原创。

如需转载，请标明出处：http://blog.csdn.net/JairusChan。

如果您对本文有任何的意见与建议，请联系笔者（JairusChan）。

http://blog.csdn.net/jairuschan/article/details/7517773/