线段树入门

Posted 2020-09-19 xFANx

一。概念

线段树是用于处理区间的复杂度为O(log n)一类数据结构。线段树是一棵完美二叉树（区别于完全二叉树）。树上的每个节点维护一个区间，且为父亲节点的区间二等分后的其中一个子区间。

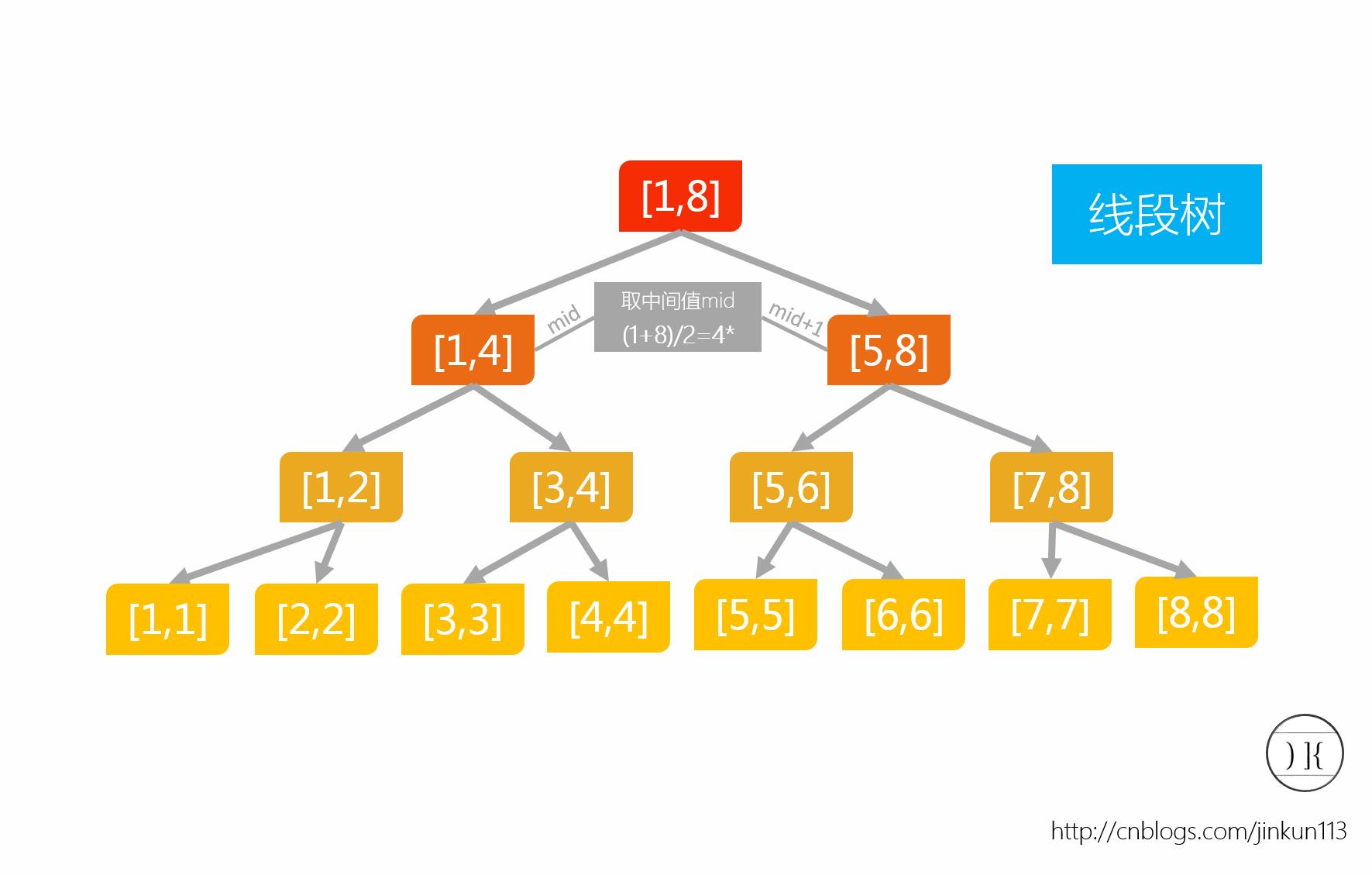
 二. 基于线段树的RMQ操作（根据维护的信息不同，线段树还可以实现其他功能）

1. 给定s和t，求a[s]~a[t]的最值
2. 给定i和x，将a[i]的值修改为x

三. 基于线段树的查询

　　例如查询区间的最小值

　　即使查询的是一个比较大的区间，由于较靠上的节点对应较大的区间，通过这些区间就可以知道大部分值中的最小值，从而可以访问较少的节点来求得最小值

 

1. 如果所查询的区间和当前区间完全没有交集，那么久返回一个不影响答案的值(如求解最小值是返回INF)
2. 如果所查询的区间完全包含了当前节点所对应的区间，那么久返回当前节点的值(例如求解区间[1,7]时，查询到的[1,4]区间的值可以直接返回）
3. 以上两种都不符合，就对两个儿子递归处理，返回两个结果中的较小者

 

 1 int n, dat[2 * maxn - 1];
 2 
 3 void init(int n_) {
 4     // 为了简单起见，把元素个数扩大到2的幂次
 5     n = 1;
 6     while (n < n_) {
 7         n *= 2;
 8     }
 9     for (int i = 0; i < 2 * n - 1; i++) {
10         dat[i] = INF;
11     }
12 }
13 
14 // 把第k个值(0 ~ indexed)更新为a
15 void update(int k, int a) {
16     // 叶子节点
17     k += n - 1;
18     dat[k] = a;
19     // 向上更新
20     while (k > 0) {
21         k = (k - 1) / 2;
22         dat[k] = min(dat[k * 2 + 1], dat[k * 2 + 2]);
23     }
24 }
25 
26 // 求[a, b]的最小值
27 // 后面的参数时为了方便计算而传入的
28 // k是节点的编号，l, r表示这个节点对应的是[l, r) 左开右闭
29 // 在外部调用时， 用(a, b, k, l, r)
30 
31 int query(int a, int b, int k, int l, int r) {
32     //如果[a, b]和[l, r]不相交，则返回一个特殊值
33     if (r <= a || b <= l) return INF;
34     
35     //如果[a, b)完全包含[l, r), 则返回当前节点的值
36     if (a <= l && r <= b) return dat[k];
37     else {
38         int vl = query(a, b, k * 2 + 1, l, (l + r) / 2);
39         int vr = query(a, b, k * 2 + 2, (l + r) / 2, r);
40         return min(vl, vr);
41     }
42 }

View Code

 

HDU-1754

典型的区间查询（最大值）和单点修改

 

挑战版

 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <vector>
 7 #define INF 0x3f3f3f3f
 8 #define mod 1000000007
 9 typedef long long LL;
10 using namespace std;
11 
12 const int maxn = 200000 + 5;
13 int n_, m, da[maxn * 4];
14 int n;
15 char op;
16 
17 void init() {
18     n = 1;
19     while (n < n_) {
20         n *= 2;
21     }
22     memset(da, -INF, sizeof(da));
23 }
24 
25 void update(int k, int val) {
26     k += n - 2;
27     da[k] = val;
28     while (k > 0) {
29         k = (k - 1) / 2;
30         da[k] = max(da[k * 2 + 1], da[k * 2 + 2]);
31     }
32 }
33 
34 int query(int a, int b, int cur, int l, int r) {
35     if (r <= a || b <= l) return -INF;
36     if (a <= l && r <= b) {
37         return da[cur];
38     } else {
39         int vl = query(a, b, cur * 2 + 1, l, (l + r) / 2);
40         int vr = query(a, b, cur * 2 + 2, (l + r) / 2, r);
41         return max(vl, vr);
42     }
43 }
44 
45 int main(int argc, const char * argv[]) {
46     while (~scanf("%d%d", &n_, &m)) {
47         init();
48         int x;
49         for (int i = 1; i <= n_; i++) {
50             scanf("%d", &x);
51             update(i, x);
52         }
53         while (m--) {
54             scanf(" %c", &op);
55             if (op == \'Q\') {
56                 int ql, qr;
57                 scanf("%d%d", &ql, &qr);
58                 printf("%d\\n", query(ql - 1, qr, 0, 0, n));
59             } else {
60                 int node, val;
61                 scanf("%d%d", &node, &val);
62                 update(node, val);
63             }
64         }
65     }
66     return 0;
67 }

View Code

 

将查询区间开为全局变量，增加建树函数

998ms

 1 #include <cstdio>
 2 #include <cstring>
 3 #define INF 0x3f3f3f3f
 4 #define max(x, y) (x > y ? x : y)
 5 typedef long long LL;
 6 using namespace std;
 7 
 8 const int maxn = 200000 + 5;
 9 int n_, m, da[maxn * 4];
10 int n, ql, qr;
11 char op;
12 
13 void init() {
14     n = 1;
15     while (n < n_) {
16         n *= 2;
17     }
18     memset(da, -INF, sizeof(da));
19 }
20 
21 void update(int k, int val) {
22     k += n - 2;
23     da[k] = val;
24     while (k > 0) {
25         k = (k - 1) / 2;
26         da[k] = max(da[k * 2 + 1], da[k * 2 + 2]);
27     }
28 }
29 
30 void build() {
31     int k = n_ + n - 2;
32     k = (k - 1) / 2;
33     while (k >= 0) {
34         da[k] = max(da[k * 2 + 1], da[k * 2 + 2]);
35         k--;
36     }
37 }
38 
39 int query(int cur, int l, int r) {
40     if (r <= ql || qr <= l) return -INF;
41     if (ql <= l && r <= qr) {
42         return da[cur];
43     } else {
44         int vl = query(cur * 2 + 1, l, (l + r) / 2);
45         int vr = query(cur * 2 + 2, (l + r) / 2, r);
46         return max(vl, vr);
47     }
48 }
49 
50 int main(int argc, const char * argv[]) {
51     while (~scanf("%d%d", &n_, &m)) {
52         init();
53         for (int i = 1; i <= n_; i++) {
54             scanf("%d", &da[i + n - 2]);
55         }
56         build();
57         while (m--) {
58             scanf(" %c", &op);
59             if (op == \'Q\') {
60                 scanf("%d%d", &ql, &qr);
61                 ql--;
62                 printf("%d\\n", query(0, 0, n));
63             } else {
64                 int node, val;
65                 scanf("%d%d", &node, &val);
66                 update(node, val);
67             }
68         }
69     }
70     return 0;
71 }

View Code

 

刘汝佳版的线段树模板。有别于挑战中，此处节点下标从1开始，查询的区间左右皆为闭区间，更新值的时候使用了递归，需要调用栈

刚学会，写的比较蠢，1357ms

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <vector>
 7 #define INF 0x3f3f3f3f
 8 #define mod 1000000007
 9 typedef long long LL;
10 using namespace std;
11 
12 const int maxn = 200000 + 5;
13 int val[4 * maxn];
14 
15 int ql, qr, p, v;
16 char op;
17 
18 int n, m;
19 
20 struct Interval {
21     
22     void update(int o, int L, int R) {
23         int M = (L + R) / 2;
24         if (L == R) {
25             val[o] = v;
26         } else {
27             if (p <= M) {
28                 update(o * 2, L, M);
29             } else {
30                 update(o * 2 + 1, M + 1, R);
31             }
32             val[o] = max(val[o * 2], val[o * 2 + 1]);
33         }
34     }
35     
36     int query(int o, int L, int R) {
37         int M = (L + R) / 2;
38         int ans = -INF;
39         if (ql <= L && R <= qr) {
40             return val[o];
41         }
42         if (ql <= M) {
43             ans = max(ans, query(o * 2, L, M));
44         }
45         if (M < qr) {
46             ans = max(ans, query(o * 2 + 1, M + 1, R));
47         }
48         return ans;
49     }
50     
51 };
52 
53 Interval tree;
54 
55 int main(int argc, const char * argv[]) {
56     while (~scanf("%d%d", &n, &m)) {
57         memset(val, 0, sizeof(val));
58         memset(&tree, 0, sizeof(tree));
59         for (int i = 1; i <= n; i++) {
60             p = i;
61             scanf("%d", &v);
62             tree.update(1, 1, n);
63         }
64         while (m--) {
65             scanf(" %c", &op);
66             if (op == \'Q\') {
67                 scanf("%d%d", &ql, &qr);
68                 printf("%d\\n", tree.query(1, 1, n));
69             } else {
70                 scanf("%d%d", &p, &v);
71                 tree.update(1, 1, n);
72             }
73         }
74     }
75     return 0;
76 }

View Code

 

HDU 2795 线段树单点

POJ 2828 线段树单点修改