单源最短路径（最短路）

Posted 2020-09-19

洛谷——P3371 【模板】单源最短路径（spfa）

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

 

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

 

输出格式：

 

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

 

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

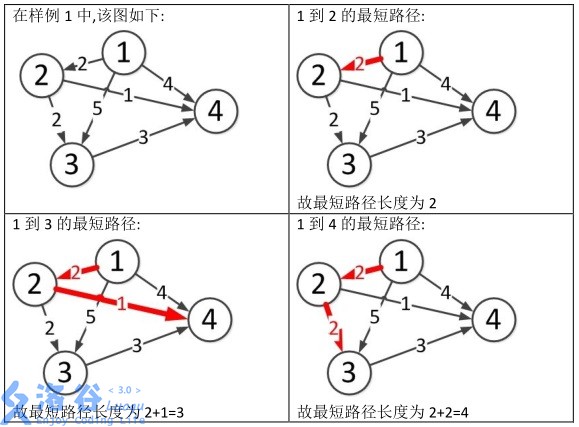
代码：

#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10001
#define maxn 2147483647LL
using namespace std;
queue<int>q; 
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<‘0‘||ch>‘9‘)
    {
        if(ch==‘-‘) f=-1;
        ch=getchar();
    }
    while(ch>=‘0‘&&ch<=‘9‘)
    {
        x=x*10+ch-‘0‘;
        ch=getchar();
    }
    return x*f;
}
struct Edge
{
    int to,ds,next;
}edge[500005];
int n,m,s,tot,x,y,z,dis[N],head[N];//n 点的个数   m 连边的条数   s 起点   dis 储存最小边 
bool vis[N];//标记一个点是否在队列中 
void add(int from,int to,int dis)
{
    tot++;
    edge[tot].to=to;
    edge[tot].ds=dis;
    edge[tot].next=head[from];
    head[from]=tot;
}//邻接链表存边 
void spfa(int s)
{
    for(int i=1;i<=n;i++) vis[i]=false,dis[i]=maxn;//初始化 
    dis[s]=0,vis[s]=true;//加入第一个点（起点）
    q.push(s);//将起点入队 
    while(!q.empty())//如果队列不为空，就接着执行操作，直到队列为空 
    {
        int x=q.front();//从队列的头元素开始进行更新最短路 
        q.pop();  //将队列头元素弹出 
        for(int i=head[x];i;i=edge[i].next)//枚举与该点连接的边 i=head[x]当前所要更新的点在队列中的位置 i=edge[i].next与当前点相连的点 
        {
            if(dis[x]+edge[i].ds<dis[edge[i].to])//如果能更新最小值 
            {
                dis[edge[i].to]=dis[x]+edge[i].ds;//更新最小值 
                if(!vis[edge[i].to])//将所能更新的没入队的元素入队 
                {    
                  vis[edge[i].to]=true;//标记为已入队
                  q.push(edge[i].to);//推入队中 
                }
            }
         } 
        vis[x]=false;//将该点标记为出队列 
    }
}
int main()
{
    n=read(),m=read(),s=read();
    for(int i=1;i<=m;i++)
    {
        x=read(),y=read(),z=read();
        add(x,y,z);//用邻接链表储存 
    }
    spfa(s);
    for(int i=1;i<=n;i++)
      printf("%d ",dis[i]);
    return 0;
 }