最大N，Insertion sort被卡

Posted 2020-09-19 浪漫逆风

本博客的代码的思想和图片参考：好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》

陈越姥姥和小伙伴们大家好。我在编写 Insert or Merge 和Insertion or Heap Sort   被测试点5：最大N，Ins卡住。难受死宝宝了。

下面是具体的图片和代码

Insert or Merge卡住：

 

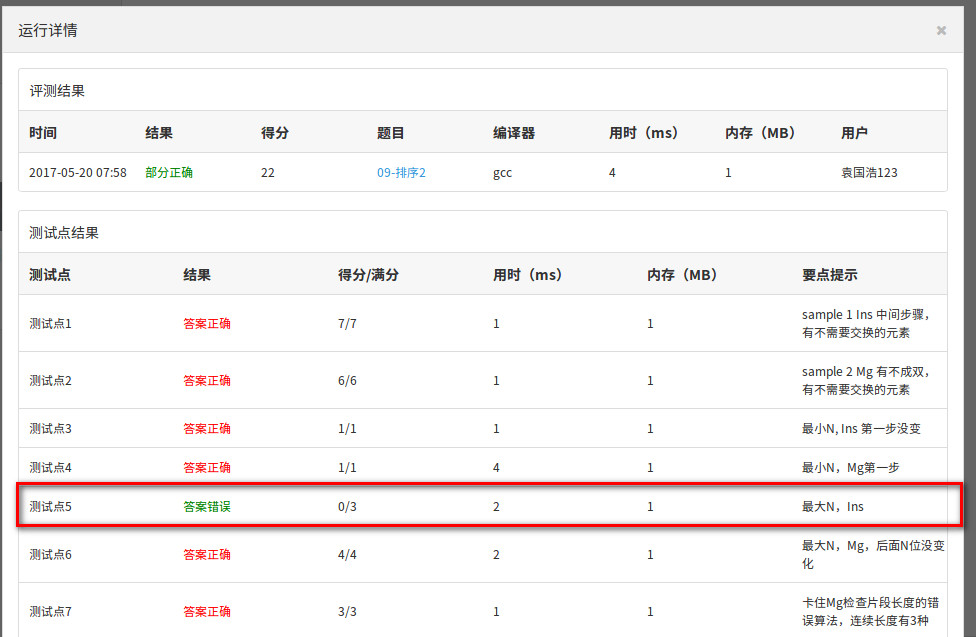
Insertion or Heap Sort 卡住：

 

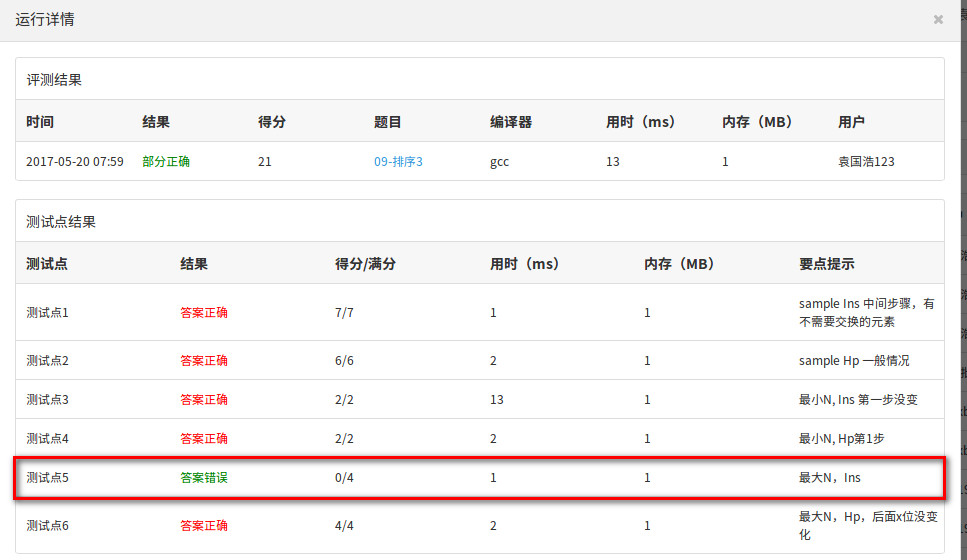
下面是具体的代码：

  1 /*
  2  * mergeOrInsert.c
  3  *
  4  *  Created on: 2017年5月19日
  5  *      Author: ygh
  6  */
  7 #include <stdio.h>
  8 #include <stdlib.h>
  9 #define MAX_LENGTH 100
 10 #define MAX_VALUE 65535
 11 typedef int elementType;
 12 
 13 /*
 14  *Get the input data from the command line
 15  *@param source A <code>elementType</code> array to store the original data
 16  *@param partical A <code>elementType</code> array to store elements which has been sorted partial
 17  *@param n The length of the array
 18  */
 19 void getInputData(elementType source[], elementType partial[], int n) {
 20     int i;
 21     elementType x;
 22     for (i = 0; i < n; i++) {
 23         scanf("%d", &x);
 24         source[i] = x;
 25     }
 26 
 27     for (i = 0; i < n; i++) {
 28         scanf("%d", &x);
 29         partial[i] = x;
 30     }
 31 }
 32 
 33 /*
 34  * Print the array to console
 35  * @param a A integer array need to sort
 36  * @param n The length of the array
 37  */
 38 void printArray(elementType a[], int n) {
 39     int i;
 40     for (i = 0; i < n; i++) {
 41         if (i == n - 1) {
 42             printf("%d", a[i]);
 43         } else {
 44             printf("%d ", a[i]);
 45         }
 46     }
 47     printf("\\n");
 48 }
 49 
 50 /*
 51  * Judge which sorting method the system has used.If it is the insertion merge,return the index
 52  * of the next insert point.Otherwise return zero
 53  * @param source A <code>elementType</code> array to store the original data
 54  * @param partical A <code>elementType</code> array to store elements which has been sorted partial
 55  * @param n The length of the array
 56  */
 57 int judgeMergeOrInsertion(elementType source[], elementType partial[], int n) {
 58     int i;
 59     int min = partial[0];
 60     int insertPoint;
 61     for (i = 1; i < n; i++) {
 62         insertPoint = i;
 63         if (partial[i] > min) {
 64             min = partial[i];
 65         } else {
 66             break;
 67         }
 68     }
 69     for (; i < n; i++) {
 70         if (partial[i] != source[i]) {
 71             return 0;
 72         }
 73     }
 74     return insertPoint;
 75 }
 76 
 77 /*
 78  * Execute one time insertion sort from insertPoint
 79  * @param partial A <code>elementType</code> array to store elements which has been sorted partial
 80  * @param inserPoint The index of next point
 81  */
 82 void insertion_sort_pass(elementType partial[], int inserPoint) {
 83     int i;
 84     int x = partial[inserPoint];
 85     for (i = inserPoint; i > 0; i--) {
 86         if (x < partial[i - 1]) {
 87             partial[i] = partial[i - 1];
 88         } else {
 89             break;
 90         }
 91     }
 92     partial[i] = x;
 93 }
 94 
 95 /*
 96  * Find the length of merge sort sub-sequence.
 97  * Algorithms thoughts:
 98  * we know the sequence length is 2 4 8 16,so we can let length from 2 4 8 ... n
 99  * 1.We judge the length whether more than 2, we check the number whether ordered between two sub-sequence. If all two sub-sequence is ordered,we will check the length whether more than four. Otherwise the length is equal two and return it.
100  * 2.we let length increase no more than n ,we can get length and return it.
101  *
102  * @param partial A <code>elementType</code> array to store elements which has been sorted partial
103  * @param n The length of the array
104  * @return The length of the sub-sequence
105  */
106 int findMergeSubSequenceLength(int partial[], int n) {
107     int length, i;
108     for (length = 2; length <= n; length *= 2) {
109         for (i = 1; i < n / length; i += 2) {
110             if (partial[i * length - 1] > partial[i * length]) {
111                 return length;
112             }
113         }
114     }
115     return n;
116 }
117 
118 /*
119  * Merge sub-sequence to original array.
120  * @param a original <code>elementType</code> array to store the elements
121  * @param tmpA temporary  <code>elementType</code> array to store the temporary elements
122  * @param l The start index of left sub-sequence
123  * @param r The start index of left sub-sequence
124  * @param rightEnd The end index of left sub-sequence
125  */
126 void merge(elementType a[], elementType tmpA[], int l, int r, int rightEnd) {
127     /*
128      * lefeEnd is the r-1,the sub-sequence is adjacent
129      */
130     int leftEnd = r - 1;
131     /*
132      * tmp is the counter of the <code>tmpA</code>
133      * we should let <code>tmpA</code> index corresponding original array
134      */
135     int tmp = l;
136     /*
137      * Record the quantity of the all elements
138      */
139     int numElements = rightEnd - l + 1;
140     int i;
141     while (l <= leftEnd && r <= rightEnd) {
142         if (a[l] <= a[r]) {
143             tmpA[tmp++] = a[l++];
144         } else {
145             tmpA[tmp++] = a[r++];
146         }
147     }
148     while (l <= leftEnd) {
149         tmpA[tmp++] = a[l++];
150     }
151     while (r <= rightEnd) {
152         tmpA[tmp++] = a[r++];
153     }
154 
155     /*
156      * Put <code>tmpA</code> elements into the original array
157      */
158     for (i = 0; i < numElements; i++, rightEnd--) {
159         a[rightEnd] = tmpA[rightEnd];
160     }
161 }
162 
163 /*
164  *merge ordered sub-sequence
165  * @param a original <code>elementType</code> array to store the elements
166  * @param tmpA temporary  <code>elementType</code> array to store the temporary elements
167  * @param n The length of the a
168  * @param the ordered current sub-sequence length
169  */
170 void mergerPass(elementType a[], elementType tmpA[], int n, int lenth) {
171     int i, j;
172     /*
173      * The loop will stop when meet the last two ordered sub-sequence
174      * The rest may be two sub-sequence of one sub-sequence
175      */
176     for (i = 0; i <= n - 2 * lenth; i += lenth * 2) {
177         merge(a, tmpA, i, i + lenth, i + 2 * lenth - 1);
178     }
179     /*
180      *If the rest of is two sub-sequence
181      */
182     if (i + lenth < n) {
183         merge(a, tmpA, i, i + lenth, n - 1);
184     } else {
185         for (j = i; j < n; j++)
186             tmpA[j] = a[j];
187     }
188 }
189 
190 int main() {
191     elementType source[MAX_LENGTH];
192     elementType partial[MAX_LENGTH];
193     int n;
194     int length = 0;
195     elementType *tmpA;
196     scanf("%d", &n);
197     getInputData(source, partial, n);
198     int inserPoint = judgeMergeOrInsertion(source, partial, n);
199     if (inserPoint != 0) {
200         if (inserPoint < n) {
201             insertion_sort_pass(partial, inserPoint);
202         }
203         printf("Insertion Sort\\n");
204     } else {
205         tmpA = malloc(n * sizeof(elementType));
206         length = findMergeSubSequenceLength(partial, n);
207         mergerPass(partial, tmpA, n, length);
208         printf("Merge Sort\\n");
209     }
210     printArray(partial, n);
211     return 0;
212 }

Insert or Merge

 

  1 /*
  2  * InsertionOrHeap.c
  3  *
  4  *  Created on: 2017年5月20日
  5  *      Author: ygh
  6  */
  7 #include <stdio.h>
  8 #include <stdlib.h>
  9 #define MAX_LENGTH 100
 10 #define MAX_VALUE 65535
 11 typedef int elementType;
 12 
 13 /*
 14  *Get the input data from the command line
 15  *@param source A <code>elementType</code> array to store the original data
 16  *@param partical A <code>elementType</code> array to store elements which has been sorted partial
 17  *@param n The length of the array
 18  */
 19 void getInputData(elementType source[], elementType partial[], int n) {
 20     int i;
 21     elementType x;
 22     for (i = 0; i < n; i++) {
 23         scanf("%d", &x);
 24         source[i] = x;
 25     }
 26 
 27     for (i = 0; i < n; i++) {
 28         scanf("%d", &x);
 29         partial[i] = x;
 30     }
 31 }
 32 
 33 /*
 34  * Print the array to console
 35  * @param a A integer array need to sort
 36  * @param n The length of the array
 37  */
 38 void printArray(elementType a[], int n) {
 39     int i;
 40     for (i = 0; i < n; i++) {
 41         if (i == n - 1) {
 42             printf("%d", a[i]);
 43         } else {
 44             printf("%d ", a[i]);
 45         }
 46     }
 47     printf("\\n");
 48 }
 49 
 50 /*
 51  * Judge which sorting method the system has used.If it is the insertion merge,return the index
 52  * of the next insert point.Otherwise return zero
 53  * @param source A <code>elementType</code> array to store the original data
 54  * @param partical A <code>elementType</code> array to store elements which has been sorted partial
 55  * @param n The length of the array
 56  */
 57 int judgeMergeOrInsertion(elementType source[], elementType partial[], int n) {
 58     int i;
 59     int min = partial[0];
 60     int insertPoint;
 61     for (i = 1; i < n; i++) {
 62         insertPoint = i;
 63         if (partial[i] > min) {
 64             min = partial[i];
 65         } else {
 66             break;
 67         }
 68     }
 69     for (; i < n; i++) {
 70         if (partial[i] != source[i]) {
 71             return 0;
 72         }
 73     }
 74     return insertPoint;
 75 }
 76 
 77 /*
 78  * Execute one time insertion sort from insertPoint
 79  * @param partial A <code>elementType</code> array to store elements which has been sorted partial
 80  * @param inserPoint The index of next point
 81  */
 82 void insertion_sort_pass(elementType partial[], int inserPoint) {
 83     int i;
 84     int x = partial[inserPoint];
 85     for (i = inserPoint; i > 0; i--) {
 86         if (x < partial[i - 1]) {
 87             partial[i] = partial[i - 1];
 88         } else {
 89             break;
 90         }
 91     }
 92     partial[i] = x;
 93 }
 94 
 95 /*
 96  * Swap two integer number
 97  */
 98 void swap(int *a, int *b) {
 99     int temp = *a;
100     *a = *b;
101     *b = temp;
102 }
103 
104 /*
105  * We know,in the heap sort,we get the maximal value from heap,the heap size will
106  * decrease each time,So the last elements is the bigger and ordered.
107  * We can according to this to find the size of the current heap.
108  * @param partial A <code>elementType</code> array to store elements which has been sorted partial
109  * @param inserPoint The index of next point
110  */
111 int getSizeOfHeap(int partial[], int n) {
112     int max = partial[0];
113     int i;
114     for (i = n - 1; i >= 0; i--) {
115         if (partial[i] < max) {
116             return i;
117         }
118     }
119     return 0;
120 }
121 
122 /*
123  * Update the element of tree make the tree to be a maximal heap
124  * @param partial A <code>elementType</code> array to store the elements
125  * @param p The index of the element need to update
126  * @param n The length of the array
127  */
128 void percDowm(elementType partial[], int p, int n) {
129     int parent, child = 0;
130     elementType x = partial[p];
131     for (parent = p; (parent * 2 + 1) < n; parent = child) {
132         child = parent * 2 + 1;
133         if ((child != n - 1) && (partial[child] < partial[child + 1])) {
134             child++;
135         }
136         if (x >= partial[child]) {
137             break;
138         } else {
139             partial[parent] = partial[child];
140         }
141     }
142     partial[parent] = x;
143 }
144 
145 /*
146  * Execute heap sort one time
147  * @param partial A <code>elementType</code> array to store elements
148  * which has been sorted partial
149  * @param size The size of the current heap
150  */
151 void heapSortPass(int partial[], int size) {
152     swap(&partial[0], &partial[size]);
153     percDowm(partial, 0, size);
154 }
155 
156 int main() {
157     elementType source[MAX_LENGTH];
158     elementType partial[MAX_LENGTH];
159     int n;
160     int size = 0;
161     scanf("%d", &n);
162     getInputData(source, partial, n);
163     int inserPoint = judgeMergeOrInsertion(source, partial, n);
164     if (inserPoint != 0) {
165         if (inserPoint < n) {
166             insertion_sort_pass(partial, inserPoint);
167         }
168         printf("Insertion Sort\\n");
169     } else {
170         printf("Heap Sort\\n");
171         size = getSizeOfHeap(partial, n);
172         heapSortPass(partial, size);
173     }
174     printArray(partial, n);
175     return 0;
176 }

Insertion or Heap Sort