数据结构与算法系列研究五——树二叉树三叉树平衡排序二叉树AVL
Posted 精心出精品
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法系列研究五——树二叉树三叉树平衡排序二叉树AVL相关的知识,希望对你有一定的参考价值。
树、二叉树、三叉树、*衡排序二叉树AVL
一、树的定义
树是计算机算法最重要的非线性结构。树中每个数据元素至多有一个直接前驱,但可以有多个直接后继。树是一种以分支关系定义的层次结构。
a.树是n(≥0)结点组成的有限集合。{N.沃恩}
(树是n(n≥1)个结点组成的有限集合。{D.E.Knuth})
在任意一棵非空树中:
⑴有且仅有一个没有前驱的结点----根(root)。
⑵当n>1时,其余结点有且仅有一个直接前驱。
⑶所有结点都可以有0个或多个后继。
b. 树是n(n≥0)个结点组成的有限集合。
在任意一棵非空树中:
⑴有一个特定的称为根(root)的结点。
⑵当n>1时,其余结点分为m(m≥0)个互不相交的子集T1,T2,…,Tm。 每个集合本身又是一棵树,并且称为根的子树(subtree)
树的固有特性---递归性。即非空树是由若干棵子树组成,而子树又可以由若干棵更小的子树组成。
树的基本操作
1、InitTree(&T) 初始化
2、DestroyTree(&T) 撤消树
3、CreatTree(&T,F) 按F的定义生成树
4、ClearTree(&T) 清除
5、TreeEmpty(T) 判树空
6、TreeDepth(T) 求树的深度
7、Root(T) 返回根结点
8、Parent(T,x) 返回结点 x 的双亲
9、Child(T,x,i) 返回结点 x 的第i 个孩子
10、InsertChild(&T,&p,i,x) 把 x 插入到 P的第i棵子树处
11、DeleteChild(&T,&p,i) 删除结点P的第i棵子树
12、traverse(T) 遍历
树的结点:包含一个数据元素及若干指向子树的分支。
●结点的度: 结点拥有子树的数目
●叶结点: 度为零的结点
●分枝结点: 度非零的结点
●树的度: 树中各结点度的最大值
●孩子: 树中某个结点的子树的根
●双亲: 结点的直接前驱
●兄弟: 同一双亲的孩子互称兄弟
●祖先: 从根结点到某结点j 路径上的所有结点(不包括指定结点)。
●子孙: 某结点的子树中的任一结点称为该结点的子孙
●结点层次: 从根结点到某结点 j 路径上结点的数目(包括结点j)
●树的深度: 树中结点的最大层次
●有向树:结点间的连线是有向的。我们所讲的树都是有向的。
●有序树: 若树中结点的各子树从左到右是有次序的,称该树为有序树,否则为无序树
●森林: 由 m 棵互不相交的树构成 F=(T1,T2,.......Tm)
一棵树去掉根结点后就变成了森林。
二叉树的性质
二叉树的第i层结点数最多为2^(i-1)个(i>0)。
深度为K的二叉树至多有(2^k)-1个结点(K>0)。
对任何一棵二叉树,设n0,n1,n2分别是度为0,1,2的结点数,则有:n0=n2+1
证明:
∵ n= n0+ n1 + n2 (n为结点总数)
b= n1 +2 n2 (b 为分支总数)
b=n-1 (除根结点外,任一结点都有分支连入父结点)
∴ n=b+1= n1 +2 n2 +1= n0+ n1 + n2
整理得: n0 = n2 +1
具有n个结点的完全二叉树高度为![]()

具有n个结点的完全二叉树具有如下特征:
① i=1 根结点,无双亲
i>1 其双亲结点为 (PARENT(i)= ![]() )
)
② 2i>n 结点i无左孩,否则 lchild(i)=2i
③ 2i+1>n 结点i无右孩,否则 rchild(i)=2i+1
二、二叉树三序遍历
2.1.实验内容
1.用先序递归遍历法建二叉树
2.输出三序递归遍历与层次遍历节点访问次序,三序遍历要求使用非递归和递归两种!!!!!!
3.用先序,中序遍历序列建二叉树
4.后序遍历复制一棵二叉树,计算叶子个数和树的深度!!!!
5.输出后序递归遍历及层次遍历结果
2.2.输入与输出
输入:输入建立二叉树的先序序列并且带‘#’,用以建树
输出 :输出四种遍历的序列和用先序中序序列建成的二叉树
2.3.关键数据结构与算法描述
关键数据结构:二叉树的结构,节点,左孩子右孩子;栈的数据结构用以采用非递归方式遍历二叉树,循环队列的数据结构用以层次遍历二叉树。
具体代码如下:

1 typedef struct TreeNode
2 {
3 ElemType elem;
4 struct TreeNode *LChild,*RChild;
5 }BiTree,*BinaryTree; //二叉树数据结构
6 typedef struct Queue
7 {
8 BinaryTree value[MAXSIZE];
9 int front,rear;
10 }LinkQueue; //队列数据结构
11 typedef BinaryTree ElemType1; //为BinaryTree起别名
12 typedef struct Stack
13 {
14 ElemType1 StackElem[MAXSIZE];
15 int top;
16 }STACK; //栈的数据结构
算法描述:用递归方法进行先序,中序,后序遍历都十分方便与简单,因为利用了树的左右结构。若树空时什么也不做,否则,按照便利的次序依次递归访问即可,如先序遍历:

//先序递归遍历
void PreOrderTraverse(BinaryTree tree)
{
if(tree!=NULL)
{
visit(tree);
PreOrderTraverse(tree->LChild);
PreOrderTraverse(tree->RChild);
}
}
而对于非递归的三序遍历,就需要栈来做数据结构了,对于前序,中序遍历来说,只需要从根节点开始,一直往左走,直至最左边左子树为空,并且在这个过程中,若是先序遍历对于路上的节点都要访问并且入栈直至访问到到最左边的节点,然后退栈访问退栈节点的右子树;若是中序遍历则只需不断的向左走并且入栈但不访问,直至最左边,然后访问最左边节点。然后退栈并访问该节点,用同样的方法访问退栈节点的右子树。最后若栈为空,则访问完成。故此设立一个一直向左走访问并且入栈的函数如下(中序与此类似,暂不赘述):

/***一直向左走直至获得最左边的指针*************/
BinaryTree GofarleftVisit(BinaryTree tree,STACK *s)
{
if(!tree)
return NULL; //若无树直接返回
BinaryTree p=tree;
visit(p); //先访问逻辑根节点
while(p->LChild)
{
push(s,p); //把访问之后的入栈以便访问右子树
visit(p->LChild); //访问左子树
p=p->LChild; //不断向左移动直至为空
}
return p;
}
非递归先序遍历的算法为:
//用非递归法先序访问
void PreOrder(BinaryTree tree)
{
if(!tree)
return ;
STACK s;
InitStack(&s);
BinaryTree p;
p=GofarleftVisit(tree,&s); //获得最左指针
while(p)
{
if(p->RChild)
p=GofarleftVisit(p->RChild,&s); //右边继续向左走
else
if(!IsEmptyStack(&s))
{
pop(&s,p);
}
else
p=NULL; //栈空时退出
}
}
对于非递归后序遍历,根据其特点,先遍历左子树再遍历右子树,最后访问根节点。则需用两个指针cur和pre来分别标记当前指针和前一个指针的位置。注意压栈时先压根节点,再压右子树,最后左子树。若当前指针cur指向叶子节点则需访问,或者pre指针不为空并且pre指向的节点恰是当前指针指向的左或右节点则代表pre子树的下一层已经无树,并且若等于左指针则右边已无节点,(右边若有则访问完左边之后必然先访问右边而不会跳到头节点);若等于右节点,则左边已访问完或无左边(因右边先压栈)。具体代码如下:

//非递归后序遍历
void postOrder(BinaryTree tree)
{
STACK s;
InitStack(&s);
BinaryTree cur,pre=0;
push(&s,tree);
/*****用两个指针来判断,如果为叶子节点或者左右子树都访问过就访问该节点****/
while(!IsEmptyStack(&s))
{
cur=gettop(&s);
if((cur->LChild==NULL&&cur->RChild==NULL)||
(pre!=NULL&&(pre==cur->RChild||pre==cur->LChild)))
{ //注意pre只要与一个相等,若为左子树则无右子树;
//若为右子树则必然访问过左子树或无左子树
visit(cur); //如果当前结点为叶子节点或者孩子节点都已被访问就访问
pop(&s,cur);
pre=cur; //标记上次被访问的节点
}
else
{
if(cur->RChild!=NULL)
push(&s,cur->RChild); //注意先把右子树入栈再入左子树,才能保持先访问左子树后访问右子树,后进先出!
if(cur->LChild!=NULL)
push(&s,cur->LChild);
}
}
}
接下来是用队列数据结构层次遍历。其实就是迭代的过程,先访问头节点,然后进左儿子,右儿子。每次出队列后都要访问该节点,然后再看该节点是否有左右子树若有则按照先左后右的顺序进队排在队尾等待遍历然后不断地循环迭代直至队为空则遍历结束。很容易理解!
具体代码如下:

//队列进行的二叉树层次遍历
void HierarchyBiTree(BinaryTree tree)
{
LinkQueue Q; //注意此处不能是指针
InitQueue(&Q);
BinaryTree p=tree;
if (tree==NULL)
return ;
visit(p);
if (p->LChild)
EnQueue(&Q,&p->LChild); //若指针不空则入队列
if (p->RChild)
EnQueue(&Q, &p->RChild); //若指针不空则入队列
while (!IsEmpty(&Q))
{
DeQueue(&Q, &p); //弹出指针进行访问
visit(p);
if (p->LChild)
EnQueue(&Q, &p->LChild); //对指针所指的结构进行判断若左右子树不空
if (p->RChild)
EnQueue(&Q, &p->RChild); //则先进左子树,后进右子树,以保证从左到右遍历
}
}
然后关于二叉树的复制,先复制左子树,然后复制右子树,最后复制头节点;在复制左右子树的时候同时也是复制树,故可用递归实现。同理,关于求叶子节点,求树的深度也是如此用递归即可实现,复制树的具体代码如下:

/************后序遍历复制一棵二叉树*************/
void CopyBiTree(BinaryTree tree,BinaryTree &newtree)
{
BinaryTree lchild,rchild;
if(!tree)
{
newtree=NULL;
}
if(tree->LChild)//若左子树存在则递归复制
{
CopyBiTree(tree->LChild,lchild);
}
else
{
lchild=NULL; //否则为零
}
if(tree->RChild)
{
CopyBiTree(tree->RChild,rchild);
}
else
{
rchild=NULL;
}
newtree=(BinaryTree)malloc(sizeof(BiTree));
newtree->elem=tree->elem;
newtree->LChild=lchild;
newtree->RChild=rchild;
}
最后就是根据先序和中序序列建树,有一定的难度需要用到递归和分治法的一些知识。首先可以证明用先序,中序遍历序列是可以还原二叉树的,因为根据先序序列可以很清楚的知道二叉树的根节点就是第一个元素,然后以这个节点把中序序列分成两半,在这个节点左边的必是左子树(因为是中序序列),而在其右边的是右子树,而左子树右子树有是一个树,故可以在更小的范围内找到左子树的根节点,在以该节点为分界点,在更小的范围内查找下去,右子树也是如此。在递归的过程中要注意进行比较的两个序列长度必然要相等,递归终止的条件就是左边分到不能再比,右边也向右不能再比为止。这样也就在递归中建立了二叉树。具体代码如下:

//首先得到中序序列二分后左边的长度
int get_left_len(int rootpos,int in_begin,int in_end,char * pre_order,char * in_order )
{
for(int i = in_begin; i <= in_end; i++)
{
if(in_order[i] == pre_order[rootpos])
{
return i-in_begin; //以双亲节点为分界点划分,返回左边的真实长度
}
}
return -1; //若没有则返回负值,用于判断
}
void creat(BinaryTree *pnode,int pre_begin,int pre_end,int in_begin,int in_end,
char * pre_order,char * in_order)
{
*pnode =(BinaryTree)malloc(sizeof(BiTree)); //申请空间
BinaryTree temp = *pnode; //创建遍历指针
temp->elem = pre_order[pre_begin]; //开始必为根节点
temp->LChild = NULL; //一定要初始化为0
temp->RChild = NULL;
if(pre_begin == pre_end)
{
return ; //只有一个节点,则已创建完毕
}
int left_len = get_left_len(pre_begin,in_begin,in_end,pre_order,in_order);
if(left_len > 0) //若没有会返回-1;若为0,则上面已创建;否则创建左子树
{
creat(&temp->LChild,pre_begin+1,pre_begin+left_len,
in_begin,in_begin+left_len-1,pre_order,in_order);
}
if(left_len < (in_end - in_begin)) //若left_len+inbegin>in_end-1则已经结束,否则创建右子树
{
creat(&temp->RChild,pre_begin+left_len+1,pre_end,
in_begin+left_len+1,in_end,pre_order,in_order);
}
}
2.4.测试与理论
具体的测试与理论见下图
测试数据一: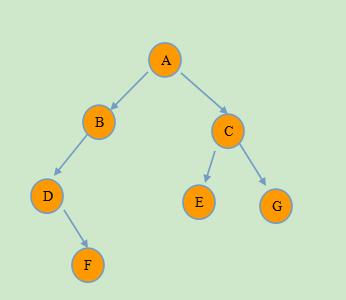
先序遍历:ABDFCEG
中序遍历:DFBAECG
后序遍历:FDBEGCA
输入数据: ABD#F###CE##G##
对于测试先序和中序序列建树的序列为
char * pre_order = "ABDEGJCFHIK";//先序序列
char * in_order = "DBGJEACFIKH"; //中序序列
输出结果截图:

测试数据二:

先序遍历:ABDEGJCFHIK
中序遍历:DBGJEACFIKH
后序遍历:DJGEBKIHFCA
输入序列:ABD##EG#J###C#F#HI#K###
输出结果见下图:
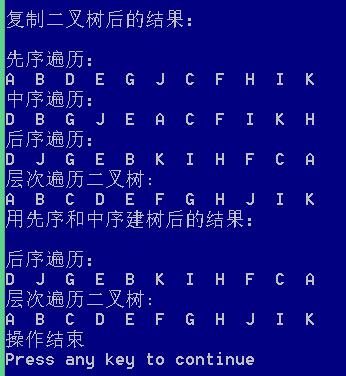
2.5.附录

1 #include "stdio.h"
2 #include "stdlib.h"
3 #include "iostream"
4 using namespace std;
5 #define MAXSIZE 100
6 #define OK 1
7 #define NO 0
8 /**********************************************/
9 typedef int status;
10 typedef char ElemType;
11 typedef struct TreeNode
12 {
13 ElemType elem;
14 struct TreeNode *LChild,*RChild;
15 }BiTree,*BinaryTree; //二叉树数据结构
16 typedef struct Queue
17 {
18 BinaryTree value[MAXSIZE];
19 int front,rear;
20 }LinkQueue; //队列数据结构
21 typedef BinaryTree ElemType1; //为BinaryTree起别名
22 typedef struct Stack
23 {
24 ElemType1 StackElem[MAXSIZE];
25 int top;
26 }STACK; //栈的数据结构
27 /************************************************/
28 /*************以下是循环队列的定义**************/
29 void InitQueue( LinkQueue *q)
30 {
31 q->front=-1; //注意初始化为-1
32 q->rear=-1;
33 }
34 status IsEmpty(LinkQueue *q)
35 {
36 if(q->rear==q->front)
37 return OK; //循环队列开始为空或者运行时出队的光标指到入队的光标
38 else
39 return NO;
40 }
41 status IsFull(LinkQueue *q)
42 {
43 if(q->front==(q->rear+1)%MAXSIZE)
44 return OK; //队满的标志就是q->front指向哑元且哑元左边为q->rear
45 else
46 return NO;
47 }
48 void EnQueue(LinkQueue *q, BinaryTree *tree)
49 {
50 if(IsFull(q))
51 return ; //入队操作,若队满则不能入队
52 q->rear=(++(q->rear))%MAXSIZE; //注意一定要先自加,再赋值
53 q->value[q->rear]=*tree;
54 }
55 void DeQueue(LinkQueue *q, BinaryTree *tree)
56 {
57 if(IsEmpty(q))
58 return ;
59 q->front=(++q->front)%MAXSIZE;
60 *tree=q->value[q->front]; //注意tree是指向指针的指针,不然将出错
61 }
62 /**************************************************************/
63 /******************以下是栈的定义******************************/
64 void InitStack(STACK *s)
65 {
66 s->top=-1; //初始化
67 }
68 void push(STACK *s,ElemType1 e)
69 {
70 if(s->top>=MAXSIZE-1)
71 return ;
72 s->StackElem[++s->top]=e; //压栈
73 }
74 void pop(STACK *s,ElemType1 &e)
75 {
76 if(s->top<=-1)
77 return ;
78 e=s->StackElem[s->top]; //出栈
79 s->top--;
80 }
81 ElemType1 gettop(STACK *s)
82 {
83 return s->StackElem[s->top]; //获得栈顶元素
84 }
85 status IsEmptyStack(STACK *s) //判断是否栈空
86 {
87 if(s->top==-1)
88 return OK;
89 else
90 return NO;
91 }
92 /******************************************************************/
93 /***************递归创建二叉树,要求读入先序序列和‘#’****************/
94 BinaryTree CreatTree(BinaryTree tree)
95 {
96 char ch;
97 if((ch=getchar())==\'#\')
98 tree=NULL;
99 else
100 {
101 tree=(BinaryTree)malloc(sizeof(BiTree));
102 tree->elem=ch;
103 tree->LChild=CreatTree(tree->LChild);
104 tree->RChild=CreatTree(tree->RChild);
105 }
106 return tree;
107 }
108 //最简单的访问二叉树
109 void visit(BinaryTree tree)
110 {
111 printf("%c ",tree->elem);
112 }
113 /**************以下是四种对二叉树的遍历方法***********************/
114 //先序递归遍历
115 void PreOrderTraverse(BinaryTree tree)
116 {
117 if(tree!=NULL)
118 {
119 visit(tree);
120 PreOrderTraverse(tree->LChild);
121 PreOrderTraverse(tree->RChild);
122 }
123 }
124
125 /***一直向左走直至获得最左边的指针*************/
126 BinaryTree GofarleftVisit(BinaryTree tree,STACK *s)
127 {
128 if(!tree)
129 return NULL; //若无树直接返回
130 BinaryTree p=tree;
131 visit(p); //先访问逻辑根节点
132 while(p->LChild)
133 {
134 push(s,p); //把访问之后的入栈以便访问右子树
135 visit(p->LChild); //访问左子树
136 p=p->LChild; //不断向左移动直至为空
137 }
138 return p;
139 }
140 //用非递归法先序访问
141 void PreOrder(BinaryTree tree)
142 {
143 if(!tree)
144 return ;
145 STACK s;
146 InitStack(&s);
147 BinaryTree p;
148 p=GofarleftVisit(tree,&s); //获得最左指针
149 while(p)
150 {
151 if(p->RChild)
152 p=GofarleftVisit(p->RChild,&s); //右边继续向左走
153 else
154 if(!IsEmptyStack(&s))
155 {
156 pop(&s,p);
157 }
158 else
159 p=NULL; //栈空时退出
160 }
161 }
162
163 //中序递归遍历
164 void InOrderTraverse(BinaryTree tree)
165 {
以上是关于数据结构与算法系列研究五——树二叉树三叉树平衡排序二叉树AVL的主要内容,如果未能解决你的问题,请参考以下文章
