排序问题1
Posted 浪漫逆风
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序问题1相关的知识,希望对你有一定的参考价值。
本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》
排序
1 排序前提
1.函数的名称规范
void X_Sort ( ElementType A[], int N )
2.大多数情况下,为简单起见,讨论从小大的整数排序
3.N是正整数
4只讨论基于比较的排序( >= < 有定义 )
5.只讨论内部排序
6稳定性:任意两个相等的数据,排序前后的相对位置不发生改变
7.没有一种排序是任何情况下都表现最好的
1 冒泡排序
1.1算法思想
第一趟:比较第一个元素和第二元素,如果第一个元素比第二个元素大,就交换位置,否则就不交换位置;在比较第二元素和第三个元素的大小,如果第二个元素比第三个元素大,交换位置,否则不交换位置;然后接着比较第三个元素和第四个元素…… 直到比较到第N-1个元素和第N个元素。这样一趟下来,可以确定最大的元素在N位置
第二趟:比较第一个元素和第二元素,如果第一个元素比第二个元素大,就交换位置,否则就不交换位置;在比较第二元素和第三个元素的大小,如果第二个元素比第三个元素大,交换位置,否则不交换位置;然后接着比较第三个元素和第四个元素……,直到比较到N-2 和N-1个元素。这样,第二趟下面,第二大的元素可以确定在N-1位置。
第三趟……
…
这样到第N趟,就可以吧数组排序完成。
1.2 伪代码描述
/*
* A method to implement bubble sort.If the bubble sort has no any swap
* operation at one time,indicating the array has been ordered.So we use a
* tag to make it effective
*@param a A integer array need to sort
*@param n The length of the array
*/
voidbubble_sort(elementType a[], int n) {
int i, j, flag;
for (i = n - 1; i >= 0; i--) {
flag = 0;
for (j = 0; j < i; j++) {
if (a[j] > a[j + 1]) {
swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (flag == 0) {
break;
}
}
}
1.3 算法分析
最好的情况:如果这个数组本身就是有序的,那么时间复杂:T=O(N)
最坏的情况:如果这个数组本身就是逆序的,那么时间复杂度为T=O(N^2)
因为只有当前面的元素严格的大于后面元素时,才会交换位置,相对位置不会发生改变,那么该算法是稳定的。
2 选择排序
2.1算法思想
选择排序的前提是保证数组中已有元素是有序的。例如在给数组的第i个元素排序(找合适位置)时,已经保证前面i-1个元素是有序的。
第一趟:当给数组中第一个元素排序时,因为就一个元素,默认就是有序的。
第二趟:当给数组中第二元素排序时,比较(前一个元素)第一个元素是否比他大,如果大,把前一个元素往后面摞一位,然后。
第三趟:给数组中第三个元素排序时,比较前一个元素是不是比他大,比他大,前一个元素向后摞一位。在比较在前面一个元素是否比他大,如果比他大,在吧在前一个元素往后摞一位;如果不比他大,那么刚才那个摞的那个空位就就放入该元素。
第四趟……
…
第N趟
2.2 伪代码描述
/*
* Implemet insertion sort.
*@param a A integer array need to sort
*@param n The length of the array
*/
voidinsertion_sort(elementType a[], int n) {
int i, j;
elementType temp;
for (i = 1; i < n; i++) {
temp = a[i];
for (j = i; j > 0 && a[j - 1] > temp; j--) {
a[j] = a[j - 1];
}
a[j] = temp;
}
}
2.3 算法分析
最好的情况:如果这个数组本身就是有序的,那么时间复杂:T=O(N)
最坏的情况:如果这个数组本身就是逆序的,那么时间复杂度为T=O(N^2)
因为只有当前面的元素严格的大于后面元素时,才会交换位置,相对位置不会发生改变,那么该算法是稳定的。
3 时间复杂的下界
为了说明这个问题,我先给出一个例题:
给定初始序列{34, 8, 64, 51,32, 21},冒泡排序和插入排序分别需要多少次元素交换才能完成?
答:冒泡需要9次,选择排序也需要9次。这是一个巧合吗?
3.1 引入概念
对于下标i<j,如果A[i]>A[j],则称(i,j)是一对逆序对(inversion)
问题:序列{34, 8, 64, 51, 32, 21}中有多少逆序对?
(34, 8) (34, 32) (34, 21) (64, 51) (64, 32) (64, 21) (51, 32) (51, 21) (32, 21)
有九个逆序对。
交换两个相邻的逆序对正好消去一个逆序对!
插入排序(冒泡排序)的时间复杂度可以重新定义为:
T(N,I)=O(N,I).I为N个元素中逆序对的个数
——如果需要排序的序列基本有序,则插入排序简单且高效
3.2 时间复杂度下界
定理:任意N个不同元素组成的序列平均具有N ( N - 1 ) / 4 个逆序对。
定理:任何仅以交换相邻两元素来排序的算
法,其平均时间复杂度为 ( N^2 ) 。
这意味着:要提高算法效率,我们必须
1.每次消去不止1个逆序对!
2. 每次交换相隔较远的2个元素!
4 希尔排序
4.1算法思想
定义增量序列 D M > D M-1 > ... > D 1 = 1
对每个 D k 进行“D k -间隔”排序 ( k = M, M-1, ... 1 )
注意:“D k -间隔”有序的序列,在执行“D k-1 -间隔”排序后,仍然是“D k -
间隔”有序的。下面用一幅图片来说明希尔排序的过程
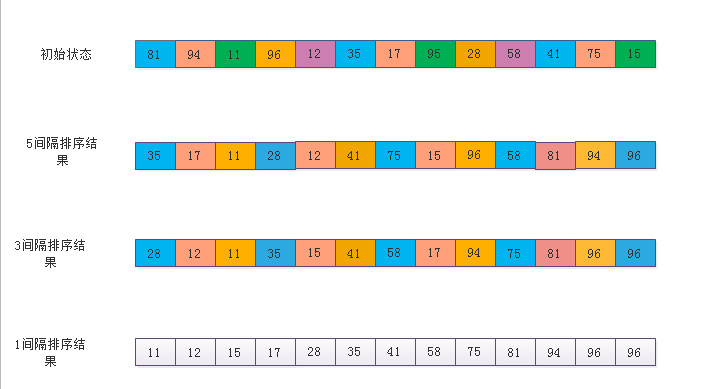
4.2希尔排序的伪代码描述
4.2.1基本的希尔排序的伪代码
/*
* Implement base shell sort
*@param a A integer array need to sort
*@param n The length of the array
*/
voidshell_sort_base(elementType a[], int n) {
int i, j, d;
elementType temp;
for (d = n / 2; d > 0; d = d / 2) {
for (i = d; i < n; i++) {
temp = a[i];
for (j = i; j >= d && a[j - d] > temp; j -= d) {
a[j] = a[j - d];
}
a[j] = temp;
}
}
}
在基本的希尔排序中,我们的间隔取 n/2 n/4 n/8 … n/2^i … 1
在上面基本的希尔排序中,最坏的时间复杂度T(n)=O(n^2).很糟糕
下面举一个最坏情况的例子

4.3 希尔排序的增量序列

5 堆排序
5.1 引子
在介绍堆排序之前,我们先介绍一下选择排序。
选择排序的算法思想:第一次从N个元素中选择一个最小的。放入0位置,第二次从N个元素中选择第二小的,放入1位置。… 第i次从N个元素选择第i小的元素放入第i-1位置
下面是选择排序的伪代码描述
void Selection_Sort ( ElementType A[], int N )
{
for ( i = 0; i < N; i ++ ) {
MinPosition = ScanForMin( A, i, N–1 );
/* 从A[i]到A[N–1]中找最小元,并将其位置赋给MinPosition */
Swap( A[i], A[MinPosition] );
/* 将未排序部分的最小元换到有序部分的最后位置 */
}
}
对于交换元素的操作,是线性。问题在于从N个元素每次找到最i小的元素。选择排序比较暴力,他每次都是从N个元素中选择最小的元素,然后进行交换位置。这样时间时间复杂度T(N)=O(N^2).我们如果改进找到最小元的操作?
答案是使用我们以前学过的工具,最小堆。
5.2 堆排序算法1---利用最小堆
算法思想:把用户给定的数组调整成一个最小堆,每次从堆中弹出一个最小的元素,使用临时数组保存,然后在吧临时数组的元素复制回原数组。
伪代码描述:
void Heap_Sort ( ElementType A[], int N )
{
BuildHeap(A); /* O(N) */
for ( i=0; i<N; i++ )
TmpA[i] = DeleteMin(A); /* O(logN) */
for ( i=0; i<N; i++ ) /* O(N) */
A[i] = TmpA[i];
}
通过伪代码我们可以看到,此算法的时间复杂的度为T(N)=O(NlogN),但是他需要开辟一个临时的数组O(N)来存放已经排序好的元素。而且还修养话费元素复制的时间。
5.3 堆排序算法2---利用最大堆
算法思想:首先吧数组调整成最大堆。把最大堆的第一个元素和最后一个元素调换位置。这样最大的元素就在原数组的最后。然后吧剩下n-1个元素调整成最大堆。重复上面的操作。这样每次选出最大的元素。
伪代码描述:
void Heap_Sort ( ElementType A[], int N )
{
for ( i=N/2-1; i>=0; i-- )/* BuildHeap */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
Swap( &A[0], &A[i] ); /* DeleteMax */
PercDown( A, 0, i );
}
}
5.3 算法分析
1.定理:堆排序处理N个不同元素的随机排列的平均比较次数是2N logN - O(Nlog logN) 。
2.虽然堆排序给出最佳平均时间复杂度,但实际效果不如用Sedgewick增量序列的希尔排序。
3.堆排序好处是取出前i个最小的数。
6 归并排序
6.1有序子列归并
在介绍归并排序的算法之前,我们先来介绍一下“有序子列的归并”下面通过一张图片来介绍
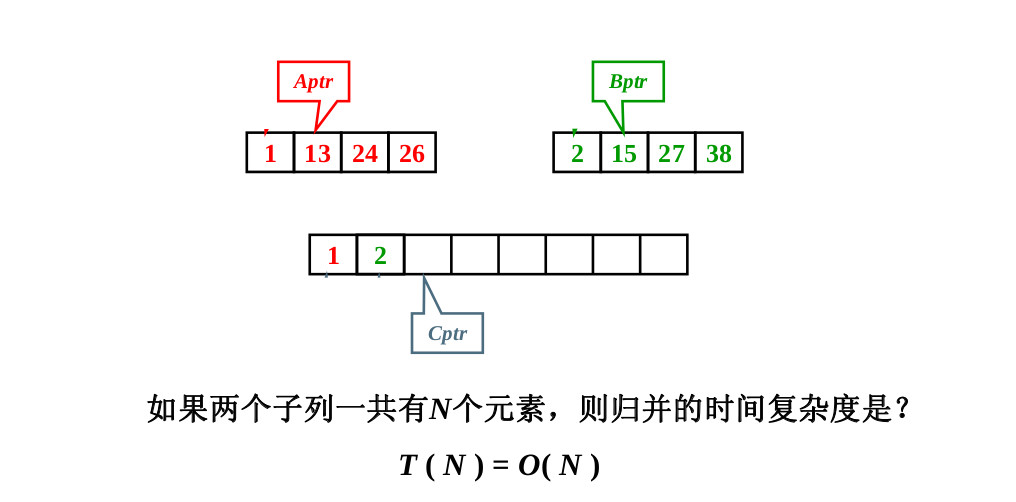
下面是给出有序子列归并的源代码
/*
* Merge sub-sequence to original array.
* @param a original <code>elementType</code> array to store the elements
* @param tmpA temporary <code>elementType</code> array to store the temporary elements
* @param l The start index of left sub-sequence
* @param r The start index of left sub-sequence
* @param rightEnd The end index of left sub-sequence
*/
voidmerge(elementType a[], elementType tmpA[], int l, int r, int rightEnd) {
/*
* lefeEnd is the r-1,the sub-sequence is adjacent
*/
int leftEnd = r - 1;
/*
* tmp is the counter of the <code>tmpA</code>
* we should let <code>tmpA</code> index corresponding original array
*/
int tmp = l;
/*
* Record the quantity of the all elements
*/
int numElements = rightEnd - l + 1;
int i;
while (l <= leftEnd && r <= rightEnd) {
if (a[l] <= a[r]) {
tmpA[tmp++] = a[l++];
} else {
tmpA[tmp++] = a[r++];
}
}
while (l <= leftEnd) {
tmpA[tmp++] = a[l++];
}
while (r < rightEnd) {
tmpA[tmp++] = a[r++];
}
/*
* Put <code>tmpA</code> elements into the original array
*/
以上是关于排序问题1的主要内容,如果未能解决你的问题,请参考以下文章