HDU 1180 诡异的楼梯（搜索）

Posted 2020-09-18 EricJeffrey

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了HDU 1180 诡异的楼梯（搜索）相关的知识，希望对你有一定的参考价值。

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1180

TLE n次。。

注意两点：1，S.T这三种位置是可以停留一秒的。即在没有路可走的时候可以停留一秒。

　　　　　2， bfs宽搜应该使用优先队列，并且vis标记加在将next节点push到队列中的时候。

然后就是奇偶判断什么的就可以了。

代码：

  1 #define _CRT_SECURE_NO_WARNINGS
  2 #include <functional>
  3 #include <algorithm>
  4 #include <iostream>
  5 #include <cstring>
  6 #include <cassert>
  7 #include <cstdio>
  8 #include <cctype>
  9 #include <vector>
 10 #include <string>
 11 #include <queue>
 12 #include <stack>
 13 #include <cmath>
 14 #include <map>
 15 #include <set>
 16 using namespace std;
 17 #define rep(i,a,n) for (int i=a;i<n;i++)
 18 #define per(i,a,n) for (int i=n-1;i>=a;i--)
 19 #define pb push_back
 20 #define mp make_pair
 21 #define all(x) (x).begin(),(x).end()
 22 #define fi first
 23 #define se second
 24 #define SZ(x) ((int)(x).size())
 25 typedef vector<int> VI;
 26 typedef long long ll;
 27 typedef pair<int, int> PII;
 28 const ll mod = 1000000007;
 29 ll powmod(ll a, ll b) { ll res = 1; a %= mod; assert(b >= 0); for (; b; b >>= 1) { if (b & 1)res = res*a%mod; a = a*a%mod; }return res; }
 30 // head
 31 const int inf = 0x3f3f3f3f;
 32 #define maxn 22
 33 int iadd[] = {0, 0, 1, -1}, jadd[] = {1, -1, 0, 0};
 34 struct node{
 35     int i, j, stp;
 36     node(int ii, int jj, int sstp): i(ii), j(jj), stp(sstp) {}
 37     bool operator < (const node &t) const {
 38         return stp > t.stp;
 39     }
 40 };
 41 char maze[maxn][maxn];
 42 int n, m;
 43 int vis[maxn][maxn];
 44 bool flag = false;
 45 priority_queue<node> q;
 46 
 47 int bfs(int stai, int staj, int dsti, int dstj){
 48     if(n == 0 || m == 0) return 0;
 49     if(n == 1 && m == 1) return 0;
 50     flag = false;
 51     memset(vis, 0, sizeof(vis));
 52     while(!q.empty()) q.pop();
 53     vis[stai][staj] = 1;
 54     q.push(node(stai, staj, 0));
 55     
 56     int maxqsize = 0;
 57     while(!q.empty()){
 58 //        maxqsize = max(maxqsize, (int)q.size());
 59         node tmn = q.top();
 60         q.pop();
 61 //        q.push(node(tmn.i, tmn.j, tmn.stp + 1));
 62         if(tmn.i == dsti && tmn.j == dstj){
 63 //            printf("-->%d\n", maxqsize); 
 64             return tmn.stp;
 65         }
 66         //printf("##\n%d\n##\n", tmn.stp);
 67         bool upd = false;
 68         for(int i = 0; i < 4; i++){
 69             int nxti = tmn.i + iadd[i];
 70             int nxtj = tmn.j + jadd[i];
 71             if(nxti < 0 || nxti >= n || nxtj < 0 || nxtj >= m)
 72                 continue;
 73             if(vis[nxti][nxtj] || maze[nxti][nxtj] == ‘*‘)
 74                 continue;
 75             if(maze[nxti][nxtj] == ‘.‘ || maze[nxti][nxtj] == ‘T‘){
 76                 upd = true;
 77                 vis[nxti][nxtj] = 1; 
 78                 q.push(node(nxti, nxtj, tmn.stp + 1));
 79             }
 80             else{
 81                 //horizontal
 82                 if(i < 2){
 83                     //next
 84                     if(nxtj < m - 1 && i == 0){
 85                         if(maze[nxti][nxtj + 1] != ‘*‘){
 86                             if(tmn.stp & 1 && maze[nxti][nxtj] == ‘|‘){
 87                                 upd = true;
 88                                 vis[nxti][nxtj + 1] = 1; 
 89                                 q.push(node(nxti, nxtj + 1, tmn.stp + 1));
 90                              }
 91                             //even
 92                             else if(!(tmn.stp & 1) && maze[nxti][nxtj] == ‘-‘){
 93                                 upd = true;
 94                                 vis[nxti][nxtj + 1] = 1;
 95                                 q.push(node(nxti, nxtj + 1, tmn.stp + 1));
 96                             }
 97                             
 98                         }
 99                     }
100                     //previous
101                     else if(nxtj > 0 && i == 1){
102                         if(maze[nxti][nxtj - 1] != ‘*‘){
103                             if(tmn.stp & 1 && maze[nxti][nxtj] == ‘|‘){
104                                 upd = true;
105                                 vis[nxti][nxtj - 1] = 1;
106                                 q.push(node(nxti, nxtj - 1, tmn.stp + 1));
107                             }
108                             //even
109                             else if(!(tmn.stp & 1) && maze[nxti][nxtj] == ‘-‘){
110                                 upd = true;
111                                 vis[nxti][nxtj - 1] = 1;
112                                 q.push(node(nxti, nxtj - 1, tmn.stp + 1));
113                             }
114                         }
115                     }
116                 }
117                 //vertical
118                 else{
119                     if(maze[nxti + 1][nxtj] != ‘*‘){
120                         if(nxti < n - 1 && i == 2){
121                             if(tmn.stp & 1 && maze[nxti][nxtj] == ‘-‘){
122                                 upd = true; 
123                                 vis[nxti + 1][nxtj] = 1;
124                                 q.push(node(nxti + 1, nxtj, tmn.stp + 1));
125                             }
126                             //even
127                             else if(!(tmn.stp & 1) && maze[nxti][nxtj] == ‘|‘){
128                                 upd = true; 
129                                 vis[nxti + 1][nxtj] = 1;
130                                 q.push(node(nxti + 1, nxtj, tmn.stp + 1));
131                             }
132                         }
133                     }
134                     //previous
135                     else if(nxti > 0 && i == 3){
136                         if(maze[nxti - 1][nxtj] != ‘*‘){
137                             if(tmn.stp & 1 && maze[nxti][nxtj] == ‘-‘){
138                                 upd = true;
139                                 vis[nxti - 1][nxtj] = 1;
140                                 q.push(node(nxti - 1, nxtj, tmn.stp + 1));
141                             }
142                             //even
143                             if(!(tmn.stp & 1) && maze[nxti][nxtj] == ‘|‘){
144                                 upd = true;
145                                 vis[nxti - 1][nxtj] = 1;
146                                 q.push(node(nxti - 1, nxtj, tmn.stp + 1));
147                             }
148                         }
149                     }
150                 }
151             }
152         }
153         if(!upd){
154             q.push(node(tmn.i, tmn.j, tmn.stp + 1));
155         }
156     }
157     
158     return 0;
159 }
160 
161 
162 int main(){
163     while(scanf("%d %d", &n, &m) != EOF){
164         memset(maze, 0, sizeof(maze));
165         int si, sj, ti, tj;
166         for(int i = 0; i < n; i++){
167             for(int j = 0; j < m; j++){
168                 scanf(" %c", &maze[i][j]);
169                 if(maze[i][j] == ‘S‘)
170                     si = i, sj = j;
171                 if(maze[i][j] == ‘T‘)
172                     ti = i, tj = j;
173             }
174         }
175         printf("%d\n", bfs(si, sj, ti, tj));
176     }    
177 }
178 
179 
180 
181 
182 
183 /*
184 5 5
185 **..T
186 **.*.
187 ..|..
188 .*.*.
189 S....
190 5 5
191 S|.|.
192 |.|*|
193 .|...
194 |***|
195 **.|T
196 3 4
197 S|.|
198 -T-.
199 .|..
200 20 20
201 S.|.|.|.|.|.|.|.|.|.
202 .|.|.|.|.|.|.|.|.|.|
203 |.|.|.|.|.|.|.|.|.|.
204 .|.|.|.|.|.|.|.|.|.|
205 |.|.|.|.|.|.|.|.|.|.
206 .|.|.|.|.|.|.|.|.|.|
207 |.|.|.|.|.|.|.|.|.|.
208 .|.|.|.|.|.|.|.|.|.|
209 |.|.|.|.|.|.|.|.|.|.
210 .|.|.|.|.|.|.|.|.|.|
211 |.|.|.|.|.|.|.|.|.|.
212 .|.|.|.|.|.|.|.|.|.|
213 |.|.|.|.|.|.|.|.|.|.
214 .|.|.|.|.|.|.|.|.|.|
215 |.|.|.|.|.|.|.|.|.|.
216 .|.|.|.|.|.|.|.|.|.|
217 |.|.|.|.|.|.|.|.|.|.
218 .|.|.|.|.|.|.|.|.|.|
219 |.|.|.|.|.|.|.|.|.|.
220 .|.|.|.|.|.|.|.|.|.T
221 5 6
222 **..|T
223 **.*..
224 ..|.-. 
225 .*.*..
226 S.....
227 20 20
228 **..**.*|.**.*.|T...
229 **.*.|....|.....*.*.
230 ..|....|...*.*.**.**
231 .*.*.**.*.**.*.|....
232 |.....*.*...|....|..
233 **..**.*|..*.*.**.*.
234 **.*.|......|....|..
235 ..|....|..**.*.|....
236 .*.*.**.*.|.....*.*.
237 |.....*.*..*|..*.*..
238 **..**.*|.**.*.|....
239 **.*.|**.*|..*.*.**.
240 **.*.*......|....|..
241 ..|....|...*.*.**.**
242 .*.*.**.*.**.*.|....
243 |.....*.*...|....|..
244 **......|...*.*.*...
245 ..|....|..**.*.|....
246 .*.*.**.*.|.....*.*.
247 S.....*.*..*|..*.*..
248 */

题目：

诡异的楼梯

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 14593 Accepted Submission(s): 3736

Problem Description

Hogwarts正式开学以后,Harry发现在Hogwarts里,某些楼梯并不是静止不动的，相反,他们每隔一分钟就变动一次方向.
比如下面的例子里,一开始楼梯在竖直方向,一分钟以后它移动到了水平方向,再过一分钟它又回到了竖直方向.Harry发现对他来说很难找到能使得他最快到达目的地的路线,这时Ron(Harry最好的朋友)告诉Harry正好有一个魔法道具可以帮助他寻找这样的路线,而那个魔法道具上的咒语,正是由你纂写的.

Input

测试数据有多组，每组的表述如下：
第一行有两个数,M和N,接下来是一个M行N列的地图,‘*‘表示障碍物,‘.‘表示走廊,‘|‘或者‘-‘表示一个楼梯,并且标明了它在一开始时所处的位置:‘|‘表示的楼梯在最开始是竖直方向,‘-‘表示的楼梯在一开始是水平方向.地图中还有一个‘S‘是起点,‘T‘是目标,0<=M,N<=20,地图中不会出现两个相连的梯子.Harry每秒只能停留在‘.‘或‘S‘和‘T‘所标记的格子内.

Output

只有一行,包含一个数T,表示到达目标的最短时间.
注意:Harry只能每次走到相邻的格子而不能斜走,每移动一次恰好为一分钟,并且Harry登上楼梯并经过楼梯到达对面的整个过程只需要一分钟,Harry从来不在楼梯上停留.并且每次楼梯都恰好在Harry移动完毕以后才改变方向.

Sample Input

5 5 **..T **.*. ..|.. .*.*. S....

Sample Output

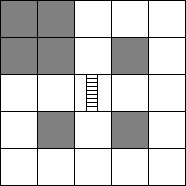
Hint

Hint

地图如下：