拓扑排序问题
Posted 浪漫逆风
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了拓扑排序问题相关的知识,希望对你有一定的参考价值。
本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》
拓扑排序
1 拓扑排序概念
首先我们来举个例子说明:计算机专业的排课
课程号 课程名称预修课程
C1 程序设计基础无
C2 离散数学无
C3 数据结构 C1, C2
C4 微积分(一) 无
C5 微积分(二) C4
C6 线性代数 C5
C7 算法分析与设计 C3
C8 逻辑与计算机设计基础无
C9 计算机组成 C8
C10 操作系统 C7, C9
C11 编译原理 C7, C9
C12 数据库 C7
C13 计算理论 C2
C14 计算机网络 C10
C15 数值分析 C6
1.拓扑序:如果图中从V到W有一条有向路径,则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。
2.获得一个拓扑序的过程就是拓扑排序
3.AOV如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph, DAG)
如果在一个图中有环路,那么,他的拓扑排序是木有的,因为下面的理论是不可能的。
2 算法思想和演示
首先我们需要根据给的关系表构建一张有向图,在有向图中,我们可以吧课程编号设置为顶点,如果该课程有直接的预修课程,我们让直接的预修课程指向该课程。下面是上面的计算机排课的有向图表示。
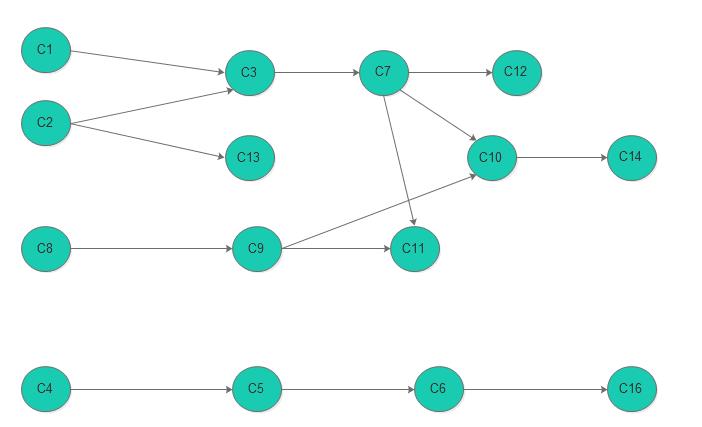
我们先找出图中没有入度的顶点并进行打印(记录),在初始情况下,有C1 C2 C8 C4 可以记录,然后在记录完以后,我们删除刚才记录和顶点和边。依次的记录或者输出输出如下

C1 C2 C8 C4
C3 C13 C9 C5
C7 C6
C12 C10 C11 C15
C14
3算法为伪代码描述
void TopSort()
{
for ( cnt = 0; cnt < |V|; cnt++ ) {
V = 未输出的入度为0的顶点; /* O(|V|) */
if ( 这样的V不存在 ) {
Error ( “图中有回路” );
break;
}
输出V,或者记录V的输出序号;
for ( V 的每个邻接点 W )
Indegree[W]––;
}
}
上面的伪代码的介绍:
1.当还没有输出(记录)到V个顶点时,就退出了,表示图有回路
2.如何实现删除已经记录的顶点--->对V进行一次记录,更新其邻接点的入度减一
3.如何实现“未输出的入度为0的顶点”如果每次都对所有的顶点进行以此遍历,那么次算法的时间复杂度为T=O(v^2),这可以不是一个非常好的算法,如何进行改进
我们可以建立一个容器,在开始或者每次入度减一时,检查是否有节点的入度变为0,如果有,就把该节点放入一个容器里面。这样这部操作就可以变成一个常数。
下面是改进以后的伪代码:
void TopSort()
{
for ( 图中每个顶点 V )
If ( Indegree[V]==0 )
Enqueue( V, Q );
while ( !IsEmpty(Q) ) {
V = Dequeue( Q );
输出V,或者记录V的输出序号; cnt++;
for ( V 的每个邻接点 W )
if ( ––Indegree[W]==0 )
Enqueue( W, Q );
}
if ( cnt != |V| )
Error( “图中有回路” );
}
改进后的算法时间复杂的为T=O(V+E)
此算法还可以用来检查有向无环图DAG(Directed Acyclic Graph)
4 关键路径问题
4.1相关概念问题
AOE(Activity On Edge)网络:一般用于安排项目的工序
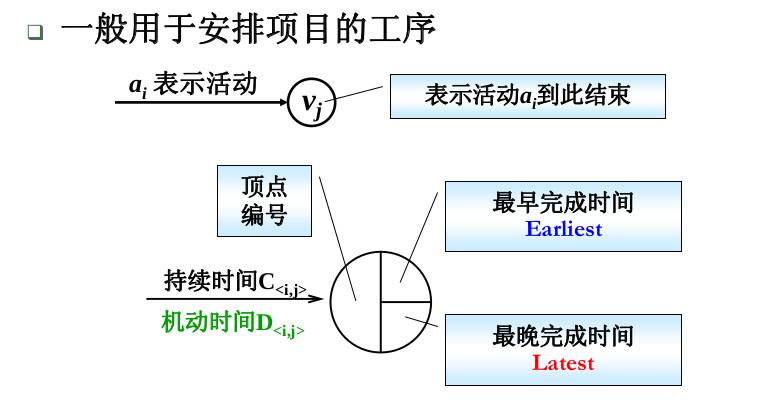
4.2 关键路径问题
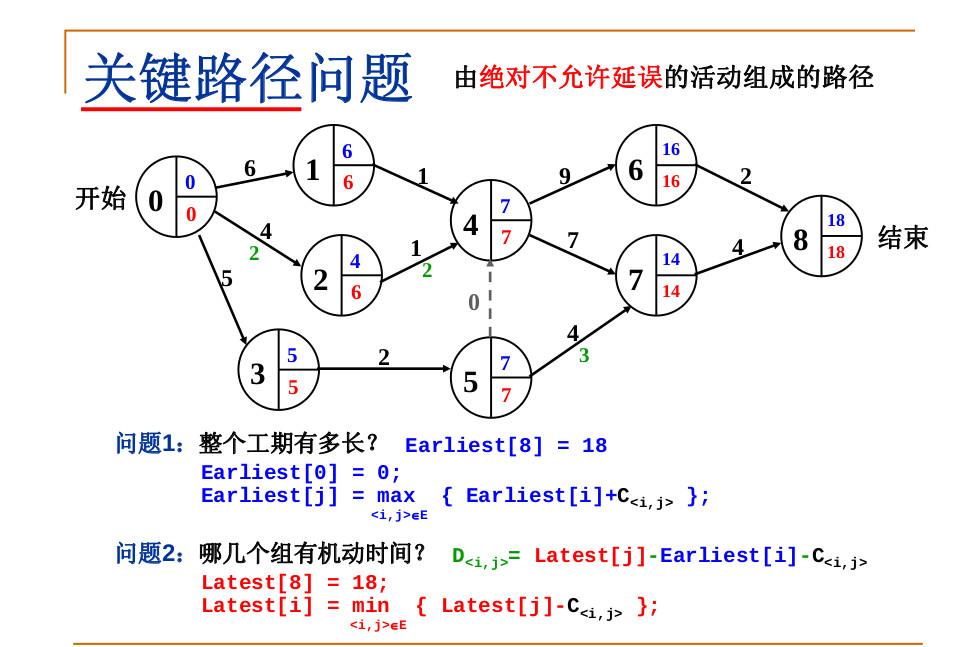
上面的说的都是理论,让我们来做一下练习吧
5 练习题
5.1
5.1.1Question
How Long Does It Take
Given the relations of all the activities of a project, you are supposed to find the earliest completion time of the project.
Input Specification:
Each
input file contains one test case. Each case starts with a line
containing two positive integers N (≤100), the number of activity
check points (hence it is assumed that the check points are numbered
from 0 to N−1), and M, the number of activities. Then M lines
follow, each gives the description of an activity. For the i-th
activity, three non-negative numbers are given: S[i],
E[i], and L[i],
where S[i] is the index of the starting
check point, E[i] of the ending check
point, and L[i] the lasting time of the
activity. The numbers in a line are separated by a space.
Output Specification:
For each test case, if the scheduling is possible, print in a line its earliest completion time; or simply output "Impossible".
Sample Input 1:
9 120 1 60 2 40 3 51 4 12 4 13 5 25 4 04 6 94 7 75 7 46 8 27 8 4
Sample Output 1:
18Sample Input 2:
4 50 1 10 2 22 1 31 3 43 2 5
Sample Output 2:
Impossible
-
时间限制:400ms
-
内存限制:64MB
-
代码长度限制:16kB
-
判题程序:系统默认
-
作者:陈越
-
单位:浙江大学
5.1.2 Algorithms Thoughts
这道题目解决的求一个工程的最早完成时间,是拓扑排序的一个变形。根据我们上面关键路径的理论知识,我们知道,最早完成时间是上一个节点的最早完成时间+持续时间中的最大值。那么我们先在原来的图的节点中添加一个字段来存储earliest,然后初始化earliest为0.在从队列中取出元素时,我们对其邻接点的earliest进行判断,让邻接点的earliest等于父节点+持续时间的最大值,并进行更新。如果最后所有的顶点都记录完毕,我们返回true,否则返回false(图有回路). 剩下的工作就是根据返回值输出所有顶点中earliest的最大值或者Impossible。弄清楚拓扑排序以后,这道题目还是很简单的。
拓扑排序的源代码:

1 /* 2 * topSort.c 3 * 4 * Created on: 2017年5月17日 5 * Author: ygh 6 */ 7 #include <stdio.h> 8 #include <stdlib.h> 9 10 #define MAX_VERTEX_NUM 10001 /*define the max number of the vertex*/ 11 #define INFINITY 65535 /*define double byte no negitive integer max number is 65535*/ 12 #define ERROR -1 13 14 typedef int vertex; /*define the data type of the vertex*/ 15 typedef int weightType; /*define the data type of the weight*/ 16 typedef char dataType; /*define the data type of the vertex value*/ 17 18 /*define the data structure of the Edge*/ 19 typedef struct eNode *ptrToENode; 20 typedef struct eNode { 21 vertex v1, v2; /*two vertex between the edge <v1,v2>*/ 22 weightType weight; /*the value of the edge\'s weight */ 23 }; 24 typedef ptrToENode edge; 25 26 /*==================A adjacent link to describe a graph=========================================*/ 27 /*define the data structure adjacent table node*/ 28 typedef struct adjNode *ptrToAdjNode; 29 typedef struct adjNode { 30 vertex adjVerx; /*the index of the vertex*/ 31 weightType weight; /*the value of the weight*/ 32 ptrToAdjNode next; /*the point to point the next node*/ 33 }; 34 35 /*define the data structure of the adjacent head*/ 36 typedef struct vNode *ptrToVNode; 37 typedef struct vNode { 38 ptrToAdjNode head; /*the point to point the adjacent table node*/ 39 dataType data; /*the space to store the name of the vertex,but some time the vertex has no names*/ 40 } adjList[MAX_VERTEX_NUM]; 41 42 /*define the data structure of graph*/ 43 typedef struct gLNode *ptrTogLNode; 44 typedef struct gLNode { 45 int vertex_number; /*the number of the vertex*/ 46 int edge_nunber; /*the number of the edge*/ 47 adjList g; /*adjacent table*/ 48 }; 49 typedef ptrTogLNode adjacentTableGraph; /*a graph show by adjacent table*/ 50 51 /* 52 create a graph given the vertex number. 53 @param vertexNum The verter number of the graph 54 @return a graph with vertex but no any egdgs 55 */ 56 adjacentTableGraph createLGraph(int vertexNum) { 57 adjacentTableGraph graph; 58 59 vertex v; 60 graph = (adjacentTableGraph) malloc(sizeof(struct gLNode)); 61 graph->vertex_number = vertexNum; 62 graph->edge_nunber = 0; 63 /*initialize the adjacent table*/ 64 for (v = 0; v < graph->vertex_number; v++) { 65 graph->g[v].head = NULL; 66 } 67 return graph; 68 } 69 70 /* 71 insert a edge to graph.We will distinct oriented graph and undirected graph 72 The e->v1 and e->v2 are the vertexs\' indexs in the adjacent table 73 @param graph The graph you want to insert edge 74 @param e The edge you want to insert the graph 75 @param isOriented Whether the graph is oriented graph.If the graph is oriented 76 we will set adjacent table graph[v1]->head=v2 and set graph[v1].head=v2 77 otherwise we only set graph[v1].head=v2 78 */ 79 void insertEdgeToLink(adjacentTableGraph graph, edge e, int isOriented) { 80 /*build node<v1,v2>*/ 81 ptrToAdjNode newNode; 82 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode)); 83 newNode->adjVerx = e->v2; 84 newNode->weight = e->weight; 85 newNode->next = graph->g[e->v1].head; 86 graph->g[e->v1].head = newNode; 87 /*if the graph is directed graph*/ 88 if (!isOriented) { 89 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode)); 90 newNode->adjVerx = e->v1; 91 newNode->weight = e->weight; 92 newNode->next = graph->g[e->v2].head; 93 graph->g[e->v2].head = newNode; 94 } 95 } 96 97 /* 98 build a graph stored by adjacent table 99 */ 100 adjacentTableGraph buildLGraph(int isOrdered) { 101 adjacentTableGraph graph; 102 edge e; 103 vertex i; 104 int vertex_num; 105 106 scanf("%d", &vertex_num); 107 graph = createLGraph(vertex_num); 108 scanf("%d", &(graph->edge_nunber)); 109 if (graph->edge_nunber) { 110 e = (edge) malloc(sizeof(struct eNode)); 111 for (i = 0; i < graph->edge_nunber; i++) { 112 scanf("%d %d", &e->v1, &e->v2); 113 e->v1--; 114 e->v2--; 115 e->weight = 1; 116 insertEdgeToLink(graph, e, isOrdered); 117 } 118 } 119 120 return graph; 121 } 122 123 /*==============================define a queue=====================================================*/ 124 /*define a list to store the element in the queue*/ 125 typedef vertex elementType; 126 typedef struct node3 *pList; 127 typedef struct node3 { 128 elementType element; 129 struct node3 *next; 130 }; 131 132 /*define a queue to point the list*/ 133 typedef struct node4 *pQueue; 134 typedef struct node4 { 135 pList front; /*the front point to point the head of the list*/ 136 pList rear; /*the rear point to point the rear of of the list*/ 137 }; 138 139 /*create a empty list to store the queue element*/ 140 pList createEmptyList() { 141 pList list; 142 list = (pList) malloc(sizeof(struct node3)); 143 list->next = NULL; 144 return list; 145 } 146 /*create a empty queye*/ 147 pQueue createEmptyQueue() { 148 pQueue queue = (pQueue) malloc(sizeof(struct node4)); 149 queue->front = NULL; 150 queue->rear = NULL; 151 return queue; 152 } 153 154 /* 155 Wether the queue is empty 156 @param queue The queue need to adjust 157 @return If the queue is null,return 1 otherwise return 0 158 */ 159 int isQueueEmpty(pQueue queue) { 160 return (queue->front == NULL); 161 } 162 163 /* 164 Add a element to a queue,If the queue is null,we will create a new queue 165 @parama queue The queue we will add elememt to 166 @prama element The element we will add to queue 167 */ 168 void addQueue(pQueue queue, elementType element) { 169 if (isQueueEmpty(queue)) { 170 pList list = createEmptyList(); 171 list->element = element; 172 queue->front = queue->rear = list; 173 } else { 174 pList newNode = (pList) malloc(sizeof(struct node3)); 175 newNode->element = element; 176 newNode->next = queue->rear->next; 177 queue->rear->next = newNode; 178 queue->rear = newNode; 179 } 180 } 181 182 /* 183 delete a element from a queue 184 @param queue The queue will be deleted a element 185 @return The element has been deleted 186 */ 187 elementType deleteEleFromQueue(pQueue queue) { 188 if (isQueueEmpty(queue)) { 189 printf("the queue is empty,don\'t allow to delete elemet from it!"); 190 return -1; 191 } else { 192 pList oldNode = queue->front; 193 elementType element = oldNode->element; 194 if (queue->front == queue->rear) { 195 queue->rear = queue->front = NULL; 196 } else { 197 queue->front = queue->front->next; 198 } 199 free(oldNode); 200 return element; 201 } 202 } 203 204 /* 205 * Top sort algorithms thoughts: 206 * 1.we first initialize all vertex in-degree is zero,then we according to 207 * the graph to set the each vertex in-degree. 208 * 2.find zero in-degree vertex and put it in queue. 209 * 3.get a vertex from a queue and record its index 210 * 4.get the all adjacent vertex of the vertex and let them in-degree decrement,at this moment,if 211 * some vertex has decrease into zero,we put them into queue. 212 * 5.Execute this operation until the queue is empty 213 * 214 * @param grap A graph which use adjacent list is used to store the vertex 215 * @param topOrder A <code>vertex</code> array to store the index of the 216 * vertex about the top queue 217 * @return If the graph is no circle,indicate the top sort is correct 1 will be return 218 * otherwise will return 0 219 */ 220 int topSort(adjacentTableGraph graph, vertex topOrder[]) { 221 vertex v; 222 ptrToAdjNode w; 223 int indegree[MAX_VERTEX_NUM], vertexConter = 0; 224 /* 225 * Create a queue to store the vertex whose in-degree is zero 226 */ 227 pQueue queue =
