二分图判定

Posted 2023-04-27

二分图：
指的是可以用两个不相交的集合表示该图的节点，然后该图的每一条边的端点分别位于这两个集合中。
判断二分图方法：
用染色法，把图中的点染成黑色和白色。
首先取一个点染成白色，然后将其相邻的点染成黑色，如果发现有相邻且同色的点，那么就退出，可知这个图并非二分图（一次bfs，O（n））。

例题：
在某学校，学生在离校之前必须做两个考试。这意味着学校必须提供一些可选的考试。每个学生必须选择两个不同的科目。根据规则每个学生不允许在同一天完成两个考试。所以学校必须安排好这些考试。
一个学校不想让老师太辛苦，他们想在两天之内安排所有这些考试。在第一天安排一些考试，在第二天安排其它的考试。要求你写一个这样的程序来看看是否可以做到让每个学生都能参加他们的考试。

输入：
在第一行有两个整数N和M,(1<=N<=200,1<=m<=30000)N代表可选择的考试的科目数量，M代表学生的人数。下面的M行中分别表示每一个学生选择的代表两个考试科目的数字。
输出：
如果安排方法存在，在第一行写"yes",在第二行输出在第一天必须安排的考试项目的数量，在第三行输出第一天代表考试科目的数字。如果存在多个安排方法，输出其中一个就可以了。
如果安排方法不存在，输出"no"

测试样例

输入

4 4
1 2
3 4
2 4
1 3
输出

是的
2
1 4

判断一个图是否是二分图 黑白染色
题意解释：给出一个图的边，对这个图进行黑白染色，不能染色则输出no
能染色输出黑色或者白色的个数，并且输出点的序号

每个人选的两个课程之间连无向边,然后DFS时进行黑白染色,DFS树上每个结点和他的父亲节点不同色.然后考虑横向边和返祖边,如果有一条边两边的结点颜色相同则说明无解,否则将白色的考试放在一天,黑色的放在另一天就可以了…

c++语言，求程序

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

int edge[201][201];
bool vis[201];
bool has[201];
int color[201]; // 0 for white, 1 for black

int main() 
int N, M;
cin >> N >> M;
memset(edge, 0, sizeof(edge));
memset(vis, 0, sizeof(vis));
memset(has, 0, sizeof(has));
for (int i = 0; i < M; i++) 
int a, b;
cin >> a >> b;
has[a] = has[b] = 1;
edge[a][b] = edge[b][a] = 1;

bool flag = true;
int counts = 0;
for (int i = 1; flag && i <= N; i++) 
if (vis[i] || !has[i]) continue;
queue<int> q;
q.push(i);
vis[i] = true;
color[i] = 0;
counts++;
while (flag && !q.empty()) 
int temp = q.front();
q.pop();
for (int j = 1; j <= N; j++) 
if (!edge[temp][j]) continue;
if (vis[j]) 
if (color[j] == color[temp]) 
flag = false;
break;

else 
continue;


vis[j] = true;
color[j] = 1 - color[temp];
counts += 1 - color[j];
q.push(j);



if (flag) 
cout << "yes" << endl;
cout << counts << endl;
bool first = true;
for (int i = 1; i <= N; i++) 
if (vis[i] == 1 && color[i] == 0) 
if (first) 
first = false;

else 
cout << " ";

cout << i;


cout << endl;

else 
cout << "no" << endl;

// system("pause");

参考技术A 二分图：
指的是可以用两个不相交的集合表示该图的节点，然后该图的每一条边的端点分别位于这两个集合中。
判断二分图方法：
用染色法，把图中的点染成黑色和白色。
首先取一个点染成白色，然后将其相邻的点染成黑色，如果发现有相邻且同色的点，那么就退出，可知这个图并非二分图（一次bfs，O（n））。

匹配：选择若干条边，然后是任意两条边无公共点
树也算是一种特殊的二分图。
求树的最大匹配用树形dp
f[i,0]表示标号为i的点不选取所能获得的最大匹配数
f[i,1]表示标号为i的点选取所能获得的最大匹配数
f[i,0]=sigmaf[k,1],f[k,0]；(k，表示以i为父节点的点的标号)f[i,1]=sigmaf[k,1],f[k,0]+1+f[j,0]；j表示与i相连的点，k是除j外的点
存储图的方法用前向星
前向星的存取：示例是以有向边为准
read(x,y);表示x，y中有一条边相连
inc（tot）；tot表示目前边的总数
e[tot]:=y；表示第tot条边以y结尾
pre[tot]:=last[x];表示与第tot条边同起点的前一条边的位置
last[x]:=tot;目前以x为起点的最后一条边是tot
tmp：=last[a];目前要访问a
while tmp<>0 do begin表示还有边
if not bl[e[tmp]] then dfs(e[tmp]);表示当前访问的点之前没有被访问过
tmp：=pre[tmp];
end;追问

用c++写一个程序好吗

HihoCoder 1121 二分图一?二分图判定

二分图一?二分图判定

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

大家好，我是小Hi和小Ho的小伙伴Nettle，从这个星期开始由我来完成我们的Weekly。

新年回家，又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表，上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字，表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好，加上相亲的人很多，所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录，即是否把两个同性安排了相亲。

OK，让我们愉快的暴力搜索吧！

才怪咧。

对于拿到的相亲情况表，我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N)，若两个人之间有一场相亲，则在对应的点之间连接一条无向边。(如下图)

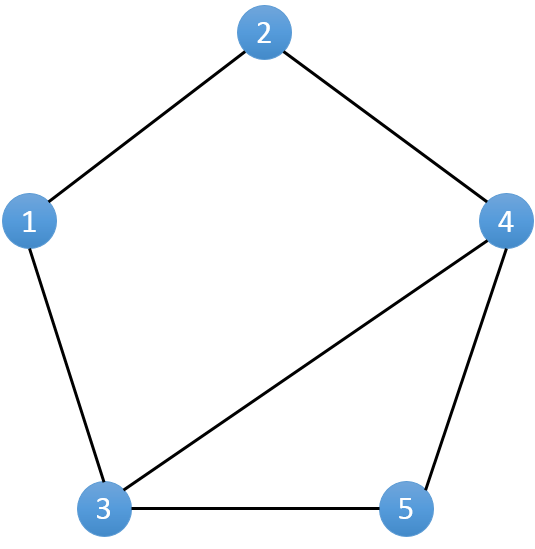
因为相亲总是在男女之间进行的，所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色，女性的节点染色黑色。对于得到的无向图来说，即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色，则表示这一条边所表示的记录有误。

由于我们并不知道每个人的性别，我们的问题就转化为判定是否存在一个合理的染色方案，使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。

那么，我们不妨将所有的点初始为未染色的状态。随机选择一个点，将其染成白色。再以它为起点，将所有相邻的点染成黑色。再以这些黑色的点为起点，将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中，我们应该怎样发现错误的记录呢？相信你一定发现了吧。对于一个已经染色的点，如果存在一个与它相邻的已染色点和它的颜色相同，那么就一定存在一条错误的记录。(如上图的4，5节点)

到此我们就得到了整个图的算法：

 

1. 选取一个未染色的点u进行染色
2. 遍历u的相邻节点v：若v未染色，则染色成与u不同的颜色，并对v重复第2步；若v已经染色，如果 u和v颜色相同，判定不可行退出遍历。
3. 若所有节点均已染色，则判定可行。

接下来就动手写写吧！

输入

第1行：1个正整数T(1≤T≤10)

接下来T组数据，每组数据按照以下格式给出：

第1行：2个正整数N,M(1≤N≤10,000，1≤M≤40,000)

第2..M+1行：每行两个整数u,v表示u和v之间有一条边

输出

第1..T行：第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”，否则输出”Wrong”

样例输入

2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5

样例输出

Wrong
Correct

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<memory>
using namespace std;
const int maxn=80010;
int col[maxn],n,m;
int Laxt[maxn],Next[maxn],To[maxn],cnt;
void add(int u,int v)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
}
void init()
{
    cnt=0;
    memset(Laxt,0,sizeof(Laxt));
    memset(col,0,sizeof(col));
}
int read()
{
    char c=getchar();int s=0;
    while(c>‘9‘||c<‘0‘) c=getchar();
    while(c>=‘0‘&&c<=‘9‘){s=s*10+c-‘0‘;c=getchar();}
    return s;
}
bool dfs(int v,int c)
{
    for(int i=Laxt[v];i;i=Next[i]){
        if(col[To[i]]==c) return false;
        if(!col[To[i]]){
            col[To[i]]=3-c;
            if(!dfs(To[i],3-c)) return false;
        }
    }
    return true;
}
bool check()
{
    for(int i=1;i<=n;i++){
        if(col[i]) continue;
        col[i]=1;
        if(!dfs(i,1)) return false;
    }
    return true;
}
int main()
{
    int i,j,T,u,v;
    scanf("%d",&T);
    while(T--){
        init();
        scanf("%d%d",&n,&m);
        for(i=1;i<=m;i++){
            u=read();v=read();
            add(u,v);add(v,u);
        }
        if(check()) printf("Correct\n");
        else printf("Wrong\n");
    }
    return 0;
}