OpenCV图像处理二十数学形态学方法(下)
Posted S大幕
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了OpenCV图像处理二十数学形态学方法(下)相关的知识,希望对你有一定的参考价值。
本篇主要讲解数学形态学方法在灰度图像中的应用。
因此,在本文中,f(x,y)不再表示二值图像,而是表示灰度图像,b(x,y)表示结构元素,其中(x,y)表示像素在图像中的坐标。
→在灰度图像形态学中,将灰度图像f(x,y)和结构元素b(x,y)看成是空间坐标(x,y)的二维函数。
1.灰度膨胀与腐蚀
→灰度膨胀和腐蚀是灰度图像形态学中的2个基本运算,其他的灰度图像形态学操作都是建立在这两种基本运算操作的基础上。
→在灰度图像形态学中,平坦结构元素(flat structure)中的"1"值指定了结构元素的邻域,也就是平坦结构元素的灰度图像形态学运算作用于灰度图像中结构元素邻域的对应像素
其中,灰度膨胀是计算结构元素邻域对应像素的灰度最大值,灰度腐蚀是计算结构元素邻域对应像素的灰度最小值。
1.1 灰度腐蚀
→在灰度形态学总,结构元素b(x,y)对二维函数f(x,y)的灰度膨胀记做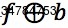 ,定义为:
,定义为:
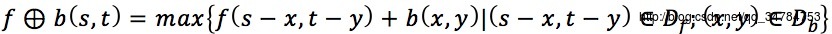
其中,Df和Db分别表示f(x,y)和b(x,y)的定义域
→Db的尺寸远小于Df的尺寸
注意:
这里f(x,y)和b(x,y)指的是函数,而不是之前二值形态学中的集合
→s(s-x,t-y)必须在f(x,y)的定义域Df内,且(x,y)必须在b(x,y)定义域Db内
→仔细观察可以看出,上面的公式与二维空域卷积十分相似,不同的是使用加法运算代替了卷积运算中的乘积运算,最大值运算代替了卷积中的求和运算。
→将上面的式子简化为以为函数表达式,可以表示为:
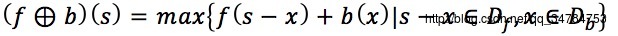
→若以b(x)滑过f(x),则在直观上更容易理解灰度膨胀的实际原理
→灰度膨胀运算以结构元素定义域内求取f+b的最大值为基础
对灰度图像进行膨胀运算的结果为:
(1.若结构元素均为正值,则输出图像比输入图像明亮。
(2.当灰暗细节尺寸小于结构元素时,灰度膨胀会消除灰暗细节部分,其程度取决于所使用结构元素的取值与形状。
→在实际应用中,灰度膨胀同市场会使用平坦的结构元素→平坦结构元素为二值矩阵。
→在这种情况下,灰度膨胀实际上是二值矩阵中1值元素在图像中对应像素的最大值运算,平坦灰度膨胀计算式可以简化为如下形式:
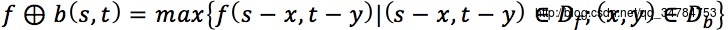
→指定b(x,y)在定义域Db内函数值为0
→平坦结构元素灰度值膨胀等效于最大值滤波,领域像素由Db的形状来决定。
1.2 灰度腐蚀
→在灰度图像形态学忠,结构元素b(x,y)对二维函数f(x,y)的灰度腐蚀,记做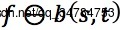 ,定义如下:
,定义如下:
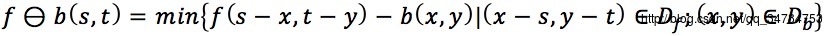
→Db与Df分别表示f(x,y)和b(x,y)的定义域
→灰度腐蚀运算以结构元素的定义域内求取f-b最小值为自己出
对一幅灰度图像进行形态学腐蚀的结果为:
(1.若结构元素均为正值,则输出图像比输入图形灰暗
(2.当明亮细节尺寸小于结构元素时,灰度腐蚀会消除明亮细节部分。
→同样,灰度腐蚀通常也使用平坦结构元素,在这种情况下,灰度腐蚀运算实际上是二值矩阵中1值元素在灰度图像中对应像素的最小值运算
→平坦灰度腐蚀可以简化为如下形式:
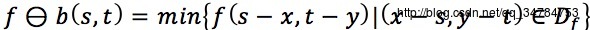
→b(x, y)在定义域Db内函数值为0
→平坦结构元素灰度值膨胀等效于最小值滤波,领域像素由Db的形状来决定。
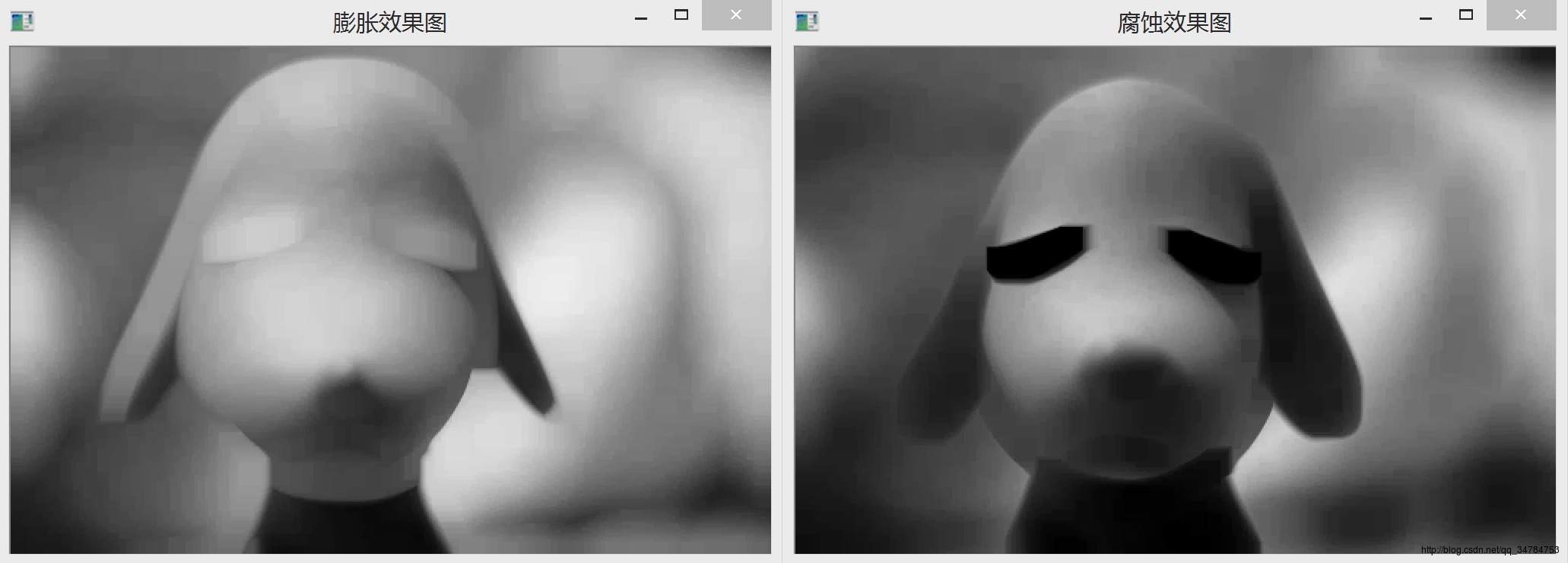
在OpenCV中,实现灰度腐蚀与灰度膨胀依然可以直接使用erode()和dilate()函数,具体程序和之前的二值图像的膨胀和腐蚀相同,只是将输入图像的二值图像改为灰度图像
具体程序如下所示:
#include <iostream>
#include <opencv2\\core\\core.hpp>
#include <opencv2\\highgui\\highgui.hpp>
#include <opencv2\\imgproc\\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg", 0);
if (!srcImage.data)
{
cout << "读入图片错误" << endl;
system("pause");
return -1;
}
Mat srcBinary;
//threshold(srcImage, srcBinary, 0, 255, THRESH_OTSU);
//imshow("原始图像", srcBinary);
//获取自定义核
Mat element = getStructuringElement(MORPH_RECT, Size(15, 15));
Mat ErodeImage;
Mat DilateImage;
erode(srcImage, ErodeImage, element);
imshow("腐蚀效果图", ErodeImage);
dilate(srcImage, DilateImage, element);
imshow("膨胀效果图", DilateImage);
waitKey();
return 0;
}
程序执行后,效果图如下所示:

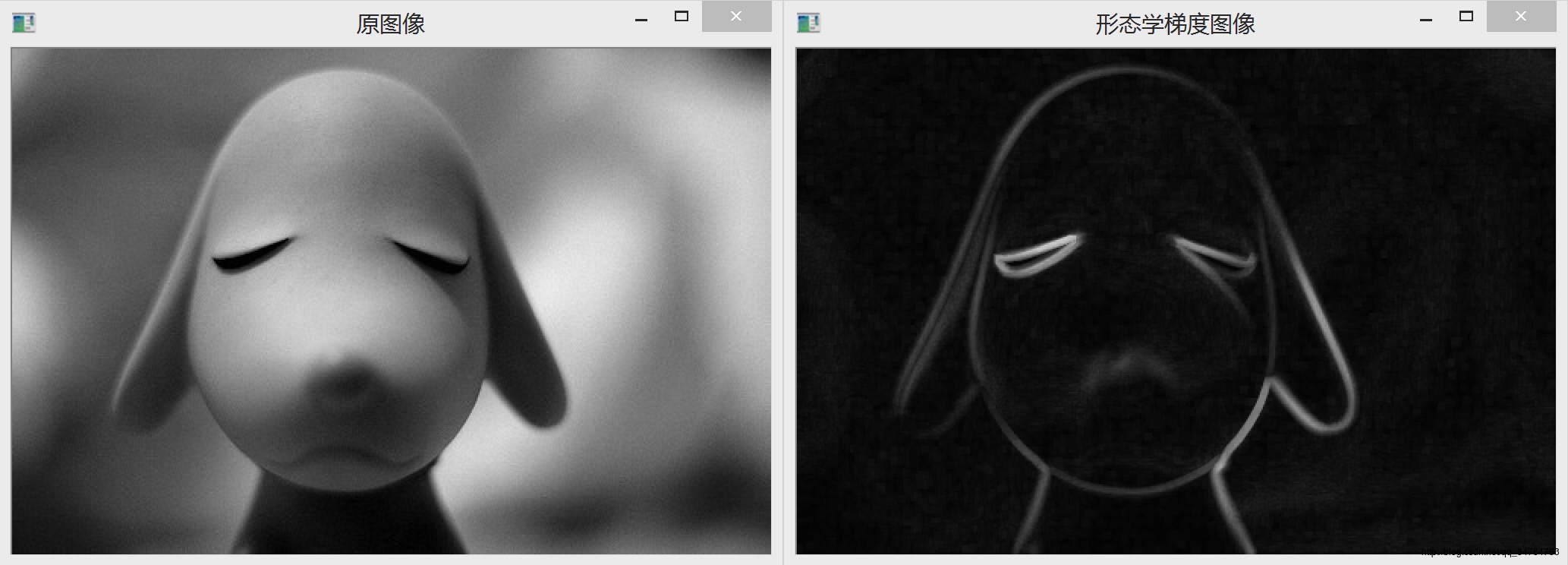
1.3 形态学梯度
在灰度图像的形态学操作中,灰度膨胀和灰度腐蚀可以结合进行使用,形态学梯度定义为灰度膨胀图像与灰度腐蚀图像的差值。
可以表示为如下形式:
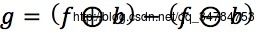
→其中g表示形态学梯度 →f表示输入图像,→b表示结构元素
∵边缘处于图像中不同灰度级的相邻区域之间,图像梯度是检测图像局部灰度级变化的量度。
→灰度膨胀扩张图像的亮区域,灰度腐蚀收缩图像的亮区域,所以二者做差突出了图像中的边缘。
→只要结构元素的尺寸适当,由于减法运算的抵消,均匀区域不会受到影响。
在OpenCV中,可以使用morphologyEx函数进行实现。具体程序如下:
//实现形态学梯度
#include <iostream>
#include <opencv2\\core\\core.hpp>
#include <opencv2\\highgui\\highgui.hpp>
#include <opencv2\\imgproc\\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg");
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
system("pause");
return -1;
}
Mat srcGray;
cvtColor(srcImage, srcGray, CV_BGR2GRAY);
//定义结构元素
Mat element = getStructuringElement(MORPH_RECT, Size(5, 5));
Mat gradImage;
morphologyEx(srcGray, gradImage, MORPH_GRADIENT, element);
imshow("原图像", srcGray);
imshow("形态学梯度图像", gradImage);
waitKey();
return 0;
}
1.4 灰度开运算与闭运算
灰度图像的开运算和闭运算与二值图像对应的运算具有相同的形式
→灰度图像的开运算定义为:
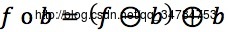
→如同在二值图像开运算中的情况,灰度开运算首先执行灰度腐蚀运算,然后执行灰度膨胀运算。
→在灰度开运算中,灰度腐蚀运算根据结构元素的尺寸和形状消除图像中的明亮细节,病史的图像整体变暗,灰度膨胀运算重新增加图像整体亮度,但不会再恢复已经消除的明亮细节。
结构元素b对灰度图像f的灰度闭运算,记做 f•b
→定义为:
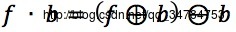
→灰度闭运算首先执行灰度膨胀运算,然后执行灰度腐蚀运算
→在灰度闭运算中,灰度膨胀根据结构元素的尺寸和形状消除图像中的灰暗细节,并使得图像整体变亮,灰度腐蚀重新降低图像的整体亮度,但是不会再回恢复已经消除的灰暗细节。
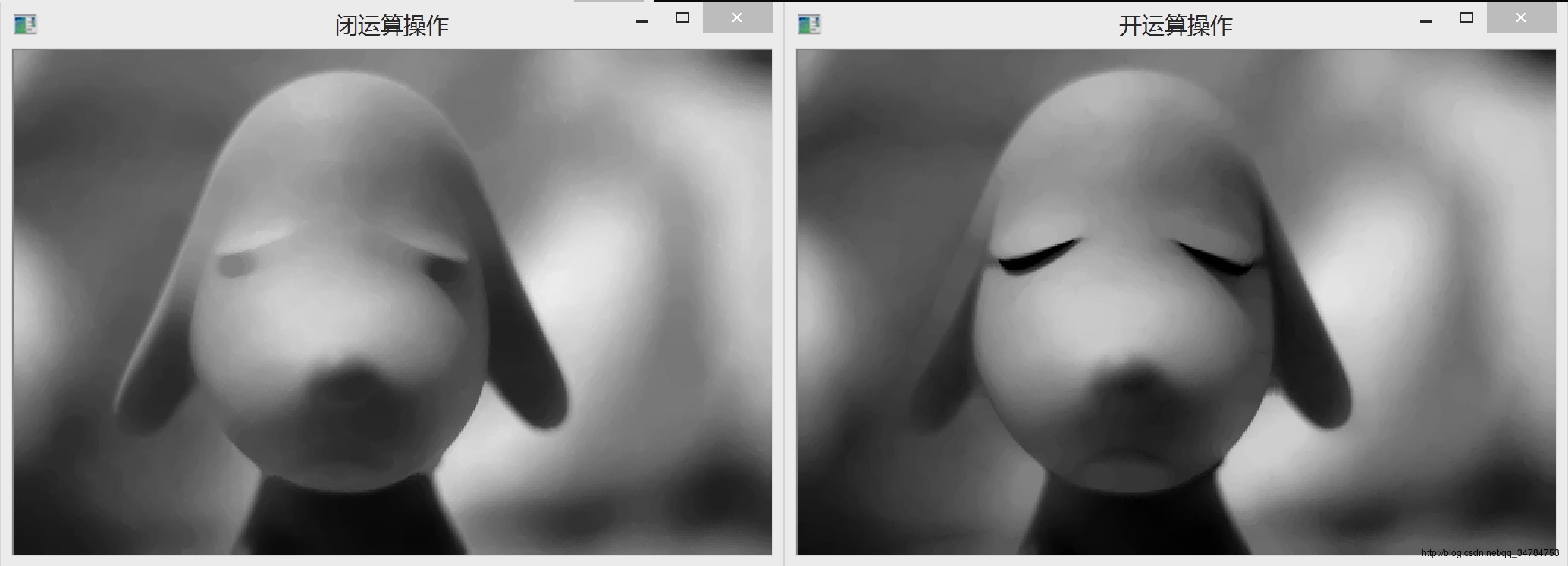
→灰度开运算消除掉了所有比圆盘直径小的波峰
作用是基本上保持图像整体灰度的条件下,消除图像中尺寸小于结构元素的明亮细节部分,而保持较大的明亮区域,灰暗细节保持不变,不受影响。
→灰度闭运算消除掉了所有比圆盘直径小的波谷
作用是基本上保持图像整体灰度的条件下,消除图像中尺寸小于结构元素的灰暗细节部分,而保持较大的灰暗区域,明亮细节保持不变,不受影响。
→最后需要说明的是,灰度图像的开运算和闭运算满足如下式子
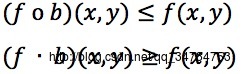
→作用与缺点:
灰度开运算会闭运算能起到图像平滑的作用,但是会破坏目标的形状和边界。
使用OpenCV实现时,与二值图像的开运算和闭运算的实现方法基本相同,只是将输入图像改为灰度图像即可。
具体程序如下:
//实现形态学开运算和闭运算
#include <iostream>
#include <opencv2\\core\\core.hpp>
#include <opencv2\\highgui\\highgui.hpp>
#include <opencv2\\imgproc\\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg");
Mat GrayImage;
cvtColor(srcImage, GrayImage,CV_BGR2GRAY);
imshow("原图像", GrayImage);
//定义结构元素
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(15, 15));
//形态学闭运算
Mat closeImage;
morphologyEx(GrayImage, closeImage, MORPH_CLOSE, element);
imshow("闭运算操作", closeImage);
//形态学开运算
Mat openImage;
morphologyEx(GrayImage, openImage, MORPH_OPEN, element);
imshow("开运算操作", openImage);
waitKey();
return 0;
}执行程序后,效果如下:

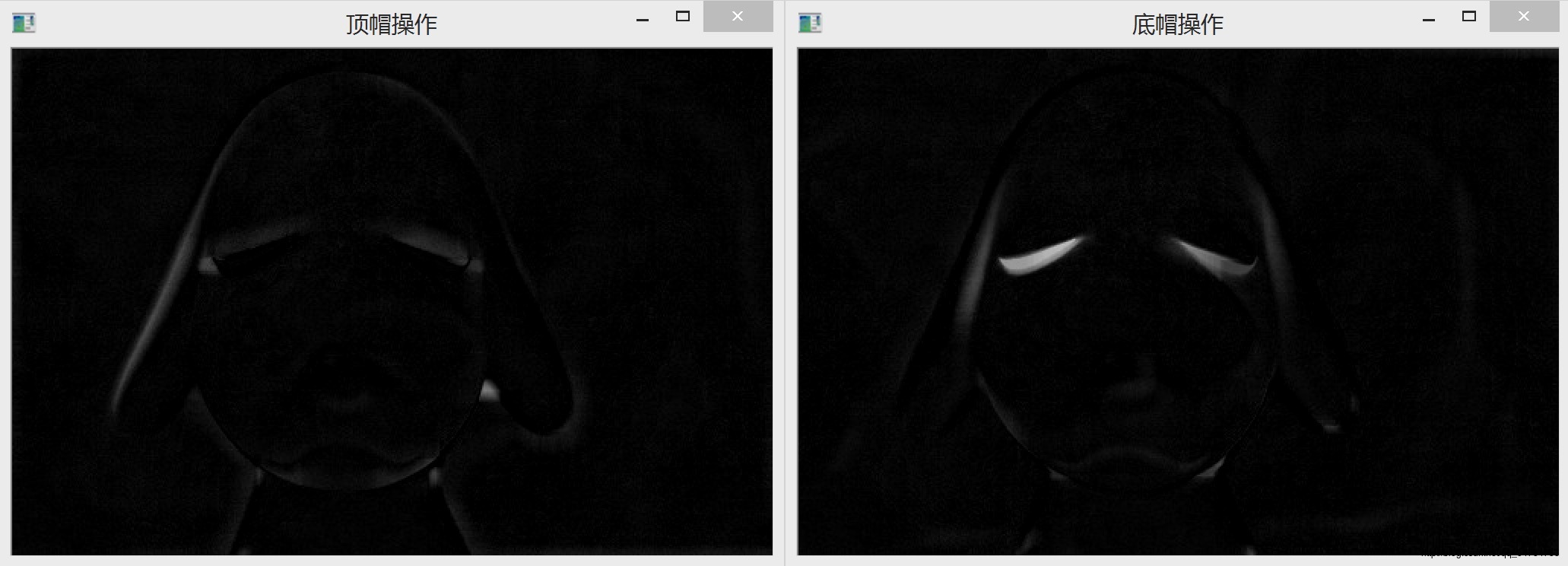
1.5 顶帽与底帽变换
→形态学顶帽变换与底帽变换是定义在灰度开运算和闭运算基础上的变换
→结构元素b对灰度图像f的顶帽变换定义为f与其灰度开运算的差值,定义为
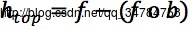
→形态学底帽变换定义为f的灰度闭运算与f本身的差值,定义为:
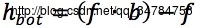
→顶帽变换与底帽变换通过图像的减法作用仅仅保留灰度开运算和闭运算中消除的明亮和灰暗目标
→顶帽变换与底帽变换能够应用于图像中的 目标提取。
→顶帽变换是用于暗北京,亮目标的情况下亮目标的提取
→底帽变换适用于亮背景,暗目标的情况下暗目标的提取
→顶帽变换的一个重要应用是消除非均匀光照的影响
→顶帽变换和底帽变换的结合使用能够应用于灰度图像的对比度增强,常用的做法是:
→→将源图像加上顶帽变换再减去底帽变换 →增强对比度。
使用OpenCV实现灰度图像的顶帽变换和底帽变换同样是使用morphologyEx()函数,具体程序如下:
//实现顶帽变换与底帽变换
#include <iostream>
#include <opencv2\\core\\core.hpp>
#include <opencv2\\highgui\\highgui.hpp>
#include <opencv2\\imgproc\\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg");
Mat GrayImage;
cvtColor(srcImage, GrayImage, CV_BGR2GRAY);
//自定义结构元素
Mat element = getStructuringElement(MORPH_RECT, Size(15, 15));
Mat topHat, bottomHat;
//进行相应操作
morphologyEx(GrayImage, topHat, MORPH_TOPHAT, element);
imshow("顶帽操作", topHat);
morphologyEx(GrayImage, bottomHat, MORPH_BLACKHAT,element);
imshow("底帽操作", bottomHat);
waitKey();
return 0;
}
1.6 形态学重构
→灰度形态学重构是一种重要的形态学变换
→灰度形态学重构是利用两幅图像来约束图像变换,其中一幅图像称为 标记图像(marker),另一幅图像称为 模板图像(mask)。
所以,灰度图像形态学重构是在模板图像的约束下,对标记图像进行处理
→设 f 和 g 分别表示标记图像和模板图像,f 和 g 尺寸相同,且对于灰度值,f ≦ g,其中,f关于 g 的一次测地膨胀定义为:
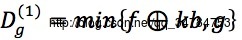
→ 其中,min中第一个参数表示结构元素b对标记图像 f 的连续k次膨胀,然后关于每一个像素(x,y)计算灰度膨胀结果与模板图像g的最小值。
→f 关于g 的n词测地膨胀定义为:
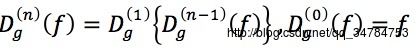
→标记图像 f 关于模板图像 g 膨胀式形态学重构定义为f 关于 g 的测地膨胀经过上式迭代过程,一直到膨胀不再发生变化,可以表示为:
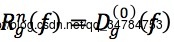
其中,n满足下式
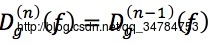
→几何意义:
(膨胀式的形态学重构对标记图像进行反复膨胀知道标记图像的边界拟合了模板图像的边界。
→开重构运算和闭重构运算是两种常用的灰度形态学重构技术
这两种重构运算都定义在膨胀式形态学重构的基础上
在开重构运算中,首先对灰度图像进行腐蚀运算,利用腐蚀图像作为标记图像,源图像作为模板图像,执行膨胀式形态学重构
灰度图像f的 k 次开重构运算,记做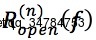 ,定义为f与k次灰度腐蚀的膨胀式形态学重构
,定义为f与k次灰度腐蚀的膨胀式形态学重构
可以表示为:
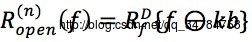
开重构运算的作用:
保持灰度腐蚀后保留的图像内容的整体形状
→同理,闭重构运算中对灰度反转图像作为模板图像,执行膨胀式形态学重构操作,然后对结果图像的灰度求反来实现比重构运算
→灰度图像 f 的k 次闭重构运算。记做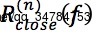 ,可以表示为:
,可以表示为:

闭重构运算的作用:
保持灰度膨胀后保留的图像内容与整体形状
→开重构和毕崇苟运算在消除尺寸小于结构元素的细节部分的同事,能够很好地保持目标的整体形状。
1.7 顶帽重构与底帽重构
顶帽重构:灰度图像f与其开重构运算之差。
底帽重构:灰度图像 f 的重构运算结果与源图像之差
可以表示为:
→顶帽重构
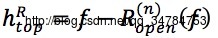
→底帽重构
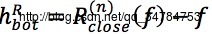
→与顶帽变换和底帽变换相比,顶帽重构与底帽重构能够更好地提取图像中亮目标与暗目标。
→顶帽重构:更完整提取出暗背景中的亮目标
→底帽重构:更完整提取出亮背景中的暗目标
以上是关于OpenCV图像处理二十数学形态学方法(下)的主要内容,如果未能解决你的问题,请参考以下文章