最小生成树之Prim算法
Posted 浪漫逆风
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最小生成树之Prim算法相关的知识,希望对你有一定的参考价值。
本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》
1 最小生成树的概念
最小生成树的概念:是由图生成而来的
是一棵树
1.无回路
2.如果有V个定点就有V-1条边
是生成树
1.包含图中所有的节点V
2.V-1条边都在图里面
3.边的权重和最小。
4.向生成树中添加任意一条边都构成回路。
2 算法思想:贪心算法
“贪”:每一步都要最好的。
“好”:权重最小的边
约束条件:
1.只能使用图里面的边
2.只能正好使用V-1条边
3.不能有回路
3 Prim算法—让一棵小树慢慢长大
3.1算法思想:
1.先选择一个顶点作为树的根节点,把这个根节点当成一棵树
2.选择图中距离这棵树最近但是没有被树收录的一个顶点,把他收录在树中,并且保证不构成回路
3.按照这样的方法,把所有的图的顶点一一收录进树中。
4.如果没有顶点可以收录
a.如果图中的顶点数量等于树的顶点数量-->最小生成树构造完成
b. 如果图中的顶点数量不等于树的顶点数量-->此图不连通
下面使用图片来具体描述此算法的算法思想:
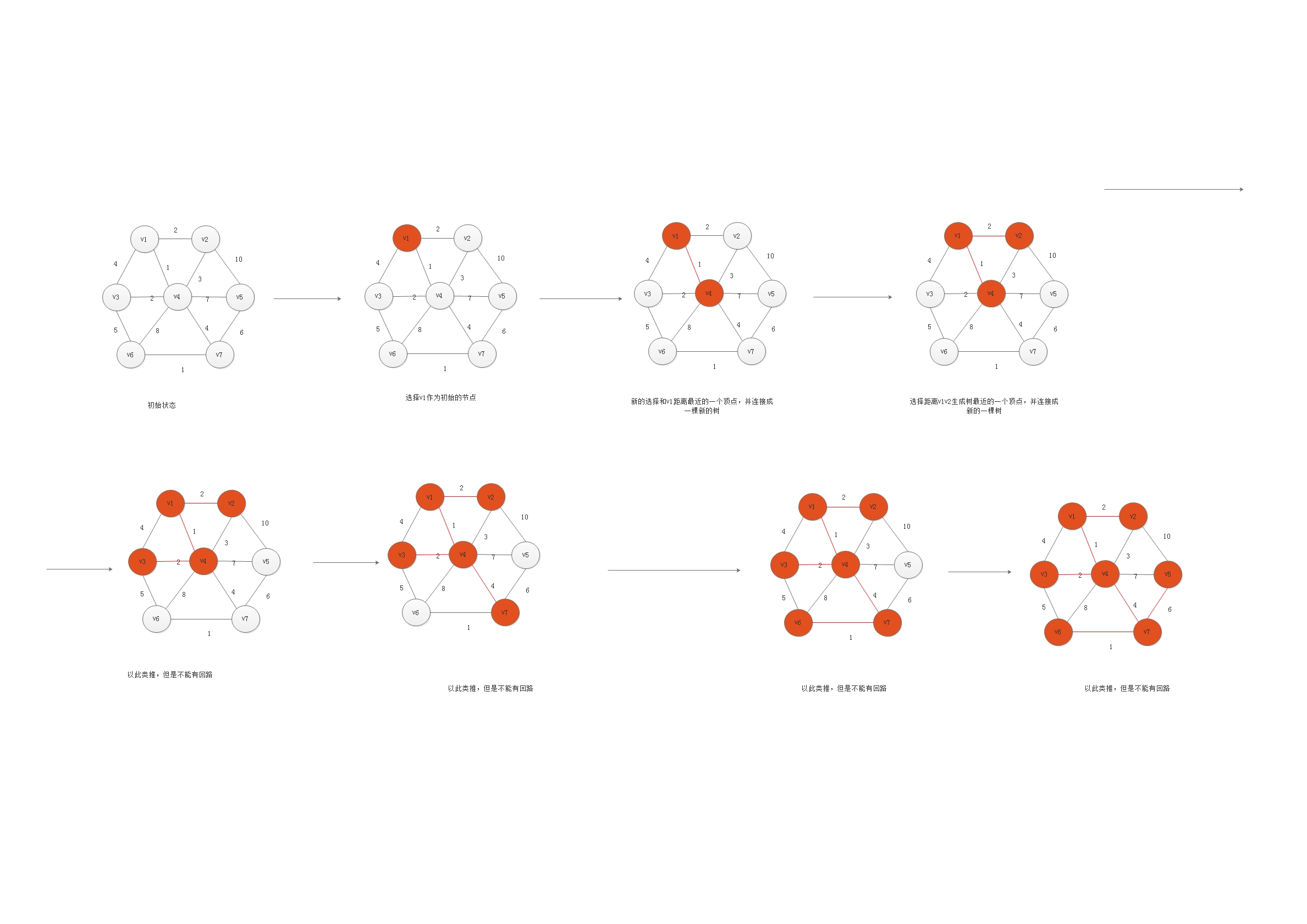
3.2Prim算法的伪代码描述
通过我们对算法的描述,我们发现Prim算法和Dijkstra算法很类似
void Prim()
{
MST = {s};
while (1) {
V = 未收录顶点中dist最小者;
if ( 这样的V不存在 )
break;
将V收录进MST: dist[V] = 0;
for ( V 的每个邻接点 W )
if ( dist[W]!=W未被收录 0 )
if ( E (V,W) < dist[W] ){
dist[W] = E (V,W) ;
parent[W] = V;
}
}
if ( MST中收的顶点不到|V|个 )
Error ( “生成树不存在” );
}
对于Prim算法
1.dist代表的是什么,应该如何被初始化
dist代表距离当前生成树的最小距离。和根节点直接相邻的初始化为权重,其他的初始化为正无穷。等每插入一个树节点,对dist进行更新。对于已经收录的节点,更新其dist=0
2.该算法的时间复杂度是多少
该算法时间复杂度在于如何去 ”未收录顶点中dist最小者”如果是使用暴力搜索的方法,那么时间复杂的为T=O(n^2).此种算法对于稠密图比较适用。
4 Kruskal 算法—将树合并成森林
4.1 算法思想
使用贪心算法,每次获取权重最小的边,但是不能让生成树构成回路。直到去到V-1条边为止。
下面还是使用一个图来说明次算法

伪代码描述
void Kruskal ( Graph G )
{
MST = { } ;
while ( MST 中不到 |V| 1 条边 && E 中还有边 ) {
从 E 中取一条权重最小的边 E (v,w) ; /* 最小堆 */
将 E (v,w) 从 E 中删除;
if ( E (V,W) 不在 MST 中构成回路) /* 并查集 */
将 E (V,W) 加入 MST;
else
彻底无视 E (V,W) ;
}
}
if ( MST 中不到 |V| 1 条边 )
Error ( “生成树不存在” );
}
如何实现“从 E 中取一条权重最小的边 E (v,w) ”---->最小堆
如何判断是否产生回路------>” 并查集”
此算法的时间复杂的为T=O(ELogE),次算法对稀疏图比较友好. 如果改图是稠密图,那么E=v^2
时间复杂度和Prim算法差不多
5 习题
下面通过一道练习题来比较Prim算法和Kruskal算法的优劣
题目的PTA链接
https://pta.patest.cn/pta/test/3512/exam/4/question/85491
题目内容:
5.1题目内容:
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 151 2 51 3 31 4 71 5 41 6 22 3 42 4 62 5 22 6 63 4 63 5 13 6 14 5 104 6 85 6 3
输出样例:
12代码可以在最后的链接里面
5.2 比较Prim算法和Kruskal算法
上面的习题其实很简单,就是Prim算法和Kruskal算法的应用。很简单,只需要改一下输出即可。
Prim算法在PTA的运行结果:
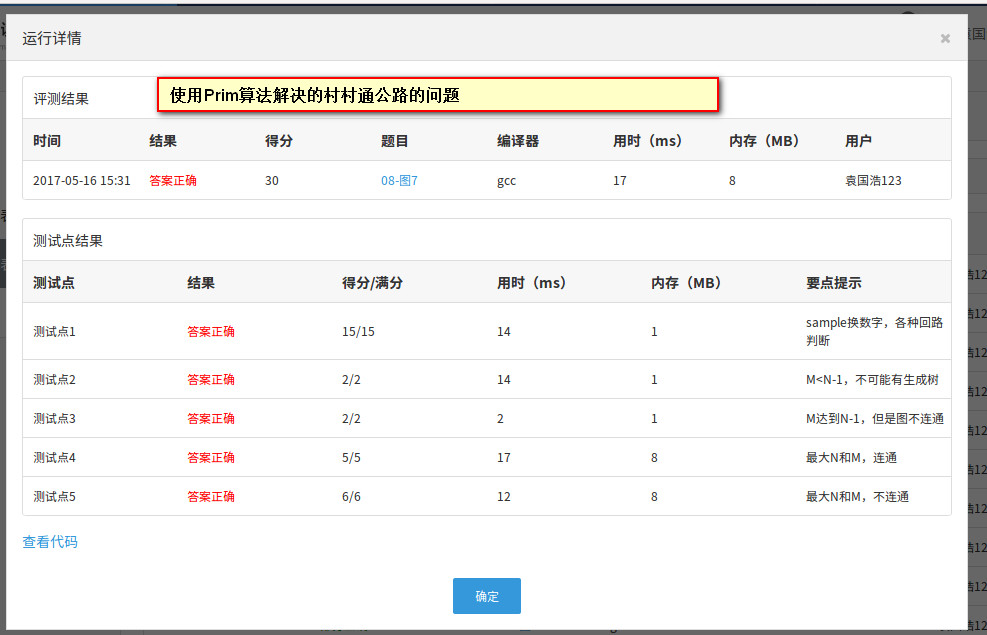
Kruskal算法在PTA的运行结果:

5.2.1空间复杂的比较
从内存的使用情况来看,Prim算法使用的邻接矩阵来存储图,Kruskal算法使用邻接表来存储图,从图中可以看出,邻接矩阵在最N时内存由1M增长到8M,而邻接表的内存始终是在1M。由此可见在同等的数据量的情况下,邻接表比邻接矩阵更加节省内存空间。
5.2.2 时间复杂的比较
就本题的测试结果来看,Kruskal算法的时间复杂度是优于Prim算法的。本题的N最大为1000
M(edge)最大为3N,远远比不上稠密图M=N^2,只能算是稀疏图。所以在稀疏图的情况下,Kruskal算法时间复杂的度较好。和理论的证明一致。
Prim算法求最小生成树的权重和打印路径代码:

1 /* 2 * prim.c 3 * 4 * Created on: 2017年5月15日 5 * Author: ygh 6 */ 7 #include <stdio.h> 8 #include <stdlib.h> 9 10 #define MAX_VERTEX_NUM 100 /*define the max number of the vertex*/ 11 #define INFINITY 65535 /*define double byte no negitive integer max number is 65535*/ 12 #define ERROR -1 13 14 typedef int vertex; /*define the data type of the vertex*/ 15 typedef int weightType; /*define the data type of the weight*/ 16 typedef char dataType; /*define the data type of the vertex value*/ 17 18 /*define the data structure of the Edge*/ 19 typedef struct eNode *ptrToENode; 20 typedef struct eNode { 21 vertex v1, v2; /*two vertex between the edge <v1,v2>*/ 22 weightType weight; /*the value of the edge\'s weight */ 23 }; 24 typedef ptrToENode edge; 25 26 /*==================A adjacent matrix to describe a graph=========================================*/ 27 28 /*define the data structure of the graph*/ 29 typedef struct gMNode *ptrTogMNode; 30 typedef struct gMNode { 31 int vertex_number; /*the number of the vertex*/ 32 int edge_nunber; /*the number of the edge*/ 33 weightType g[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*define the adjacent matrix weight of graph*/ 34 dataType data[MAX_VERTEX_NUM]; /*define the dataType array to store the value of vertex*/ 35 }; 36 typedef ptrTogMNode adjacentMatrixGraph; /*a graph show by adjacent matrix*/ 37 38 /* 39 create a graph given the vertex number. 40 @param vertexNum The verter number of the graph 41 @return a graph with vertex but no any egdgs 42 */ 43 adjacentMatrixGraph createMGraph(int vertexNum) { 44 vertex v, w; 45 adjacentMatrixGraph graph; 46 graph = (adjacentMatrixGraph) malloc(sizeof(struct gMNode)); 47 graph->vertex_number = vertexNum; 48 graph->edge_nunber = 0; 49 /*initialize the adjacent matrix*/ 50 for (v = 0; v < graph->vertex_number; v++) { 51 for (w = 0; w < graph->vertex_number; w++) { 52 graph->g[v][w] = INFINITY; 53 } 54 } 55 56 return graph; 57 } 58 59 /* 60 insert a edge to graph.We will distinct oriented graph and undirected graph 61 @param graph The graph you want to insert edge 62 @param e The edge you want to insert the graph 63 @param isOriented Whether the graph is oriented graph.If the graph is oriented 64 we will set adjacent matrix [n][m]=[m][n]=edge\'s weight,else we only set 65 the adjacent matrix [n][m]=edge\'s weight 66 */ 67 void inserEdgeToMatrix(adjacentMatrixGraph graph, edge e, int isOriented) { 68 graph->g[e->v1][e->v2] = e->weight; 69 if (!isOriented) { 70 graph->g[e->v2][e->v1] = e->weight; 71 } 72 } 73 74 /* 75 construct a graph according user\'s input 76 77 @return a graph has been filled good 78 */ 79 adjacentMatrixGraph buildMGraph(int isOrdered) { 80 adjacentMatrixGraph graph; 81 edge e; 82 vertex i; 83 int vertex_num; 84 scanf("%d", &vertex_num); 85 graph = createMGraph(vertex_num); 86 scanf("%d", &(graph->edge_nunber)); 87 if (graph->edge_nunber) { 88 e = (edge) malloc(sizeof(struct eNode)); 89 for (i = 0; i < graph->edge_nunber; i++) { 90 scanf("%d %d %d", &e->v1, &e->v2, &e->weight); 91 e->v1--; 92 e->v2--; 93 inserEdgeToMatrix(graph, e, isOrdered); 94 } 95 } 96 return graph; 97 98 } 99 100 /*==================A adjacent link to describe a graph=========================================*/ 101 /*define the data structure adjacent table node*/ 102 typedef struct adjNode *ptrToAdjNode; 103 typedef struct adjNode { 104 vertex adjVerx; /*the index of the vertex*/ 105 weightType weight; /*the value of the weight*/ 106 ptrToAdjNode next; /*the point to point the next node*/ 107 }; 108 109 /*define the data structure of the adjacent head*/ 110 typedef struct vNode *ptrToVNode; 111 typedef struct vNode { 112 ptrToAdjNode head; /*the point to point the adjacent table node*/ 113 dataType data; /*the space to store the name of the vertex,but some time the vertex has no names*/ 114 } adjList[MAX_VERTEX_NUM]; 115 116 /*define the data structure of graph*/ 117 typedef struct gLNode *ptrTogLNode; 118 typedef struct gLNode { 119 int vertex_number; /*the number of the vertex*/ 120 int edge_nunber; /*the number of the edge*/ 121 adjList g; /*adjacent table*/ 122 }; 123 typedef ptrTogLNode adjacentTableGraph; /*a graph show by adjacent table*/ 124 125 /* 126 create a graph given the vertex number. 127 @param vertexNum The verter number of the graph 128 @return a graph with vertex but no any egdgs 129 */ 130 adjacentTableGraph createLGraph(int vertexNum) { 131 adjacentTableGraph graph; 132 133 vertex v; 134 graph = (adjacentTableGraph) malloc(sizeof(struct gLNode)); 135 graph->vertex_number = vertexNum; 136 graph->edge_nunber = 0; 137 /*initialize the adjacent table*/ 138 for (v = 0; v < graph->vertex_number; v++) { 139 graph->g[v].head = NULL; 140 } 141 return graph; 142 } 143 144 /* 145 insert a edge to graph.We will distinct oriented graph and undirected graph 146 The e->v1 and e->v2 are the vertexs\' indexs in the adjacent table 147 @param graph The graph you want to insert edge 148 @param e The edge you want to insert the graph 149 @param isOriented Whether the graph is oriented graph.If the graph is oriented 150 we will set adjacent table graph[v1]->head=v2 and set graph[v1].head=v2 151 otherwise we only set graph[v1].head=v2 152 */ 153 void insertEdgeToLink(adjacentTableGraph graph, edge e, int isOriented) { 154 /*build node<v1,v2>*/ 155 ptrToAdjNode newNode; 156 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode)); 157 newNode->adjVerx = e->v2; 158 newNode->weight = e->weight; 159 newNode->next = graph->g[e->v1].head; 160 graph->g[e->v1].head = newNode; 161 /*if the graph is directed graph*/ 162 if (!isOriented) { 163 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode)); 164 newNode->adjVerx = e->v1; 165 newNode->weight = e->weight; 166 newNode->next = graph->g[e->v2].head; 167 graph->g[e->v2].head = newNode; 168 } 169 } 170 171 /* 172 build a graph stored by adjacent table 173 */ 174 adjacentTableGraph buildLGraph() { 175 adjacentTableGraph graph; 176 edge e; 177 vertex i; 178 int vertex_num; 179 180 scanf("%d", &vertex_num); 181 graph = createLGraph(vertex_num); 182 scanf("%d", &(graph->edge_nunber)); 183 if (graph->edge_nunber) { 184 e = (edge) malloc(sizeof(struct eNode)); 185 for (i = 0; i < graph->edge_nunber; i++) { 186 scanf("%d %d %d", &e->v1, &e->v2, &e->weight); 187 insertEdgeToLink(graph, e, 0); 188 } 189 } 190 191 return graph; 192 } 193 194 /* 195 * Find the minimal node closest to created tree 196 */ 197 vertex findMinDist(adjacentMatrixGraph graph, weightType dist[]) { 198 vertex minV, v; 199 weightType minDist = INFINITY; 200 for (v = 0; v < graph->vertex_number; v++) { 201 if (dist[v] != 0 && dist[v] < minDist) { 202 minDist = dist[v]; 203 minV = v; 204 } 205 } 206 if (minDist < INFINITY) { 207 return minV; 208 } else { 209 return ERROR; 210 } 211 } 212 213 /* 214 * Prim algorithms,we will store the minimal created tree with a adjacent 215 * list table and return the minimal weight 216 * @param mGraph The graph showed by adjacent matrix is to store graph 217 * @param lGraph The graph showed by adjacent list is to store the minimal created tree 218 * @return The weight of the minimal created tree if the graph is connected, otherwise return 219 * <code>ERROR</code> 220 */ 221 int prim(adjacentMatrixGraph mGraph, adjacentTableGraph lGraph) { 222 223 weightType dist[mGraph->vertex_number], totalWeight; 224<以上是关于最小生成树之Prim算法的主要内容,如果未能解决你的问题,请参考以下文章
