图论讲解——最小生成树

Posted 2020-09-18

关于这个东西，有的童鞋又要开始蒙了，最小生成树是个什么鬼？！

前面我们已经说过树是什么东西了，所谓最小生成树嘛，最小嘛，那就是所有生成的树中最小的那个呗！

太别扭了对吧？

好，我们来看看官方回答。

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

prim算法

Prim算法是通过先选取一个点，然后不断加入点的一个过程。

’初始化：V’={x},E’={},x是随便一个节点；

’重复下列操作，直到V’=V:

  ´在E集合当中选择最小的边<u,v>使得u∈V’但是v∉V’;

  ´V’加入节点v，E’加入<u,v>；

  ´（V’,E’）则为所求的最小生成树。

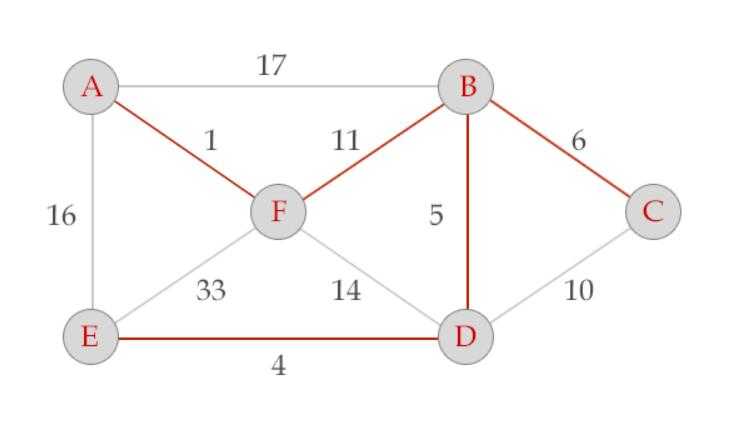
´我们可以对该算法里面的各个步骤分别考虑：

´初始化：V’={x},E’={},x是随便一个节点；

             这一步只需要随便选取一个点即可；

´重复下列操作，直到V’=V:

´在E集合当中选择最小的边<u,v>使得u∈V’但是v∉V’;

´V’加入节点v，E’加入<u,v>；

　　　　　　对于上面的第二步，实际上我们只需要对于每一个点维护一个V’集合中的点到达该点的最短距离。

　　　　　　然后每次扫描一遍数组找到我们所需要的v加入V’；

复杂度为O(N^2+M).

对于上面的第二步操作，我们实际上可以通过堆（优先队列）维护一个满足u∈V’但是v∉V’的边集，那么我们就能迅速取出满足要求的边；

然后当改变了V’的时候，我们就可以根据新加入的节点v对原有的堆进行删除和插入操作。

需要注意的是，当我们用优先队列实现的时候，我们需要将删除操作延迟。

复杂度为O((N+M)logN).

哔哔了这么多，我们直接来看看代码吧！（当然先是一些板子）