小白天堂之编写词法语法分析器何其简单
Posted 77458
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了小白天堂之编写词法语法分析器何其简单相关的知识,希望对你有一定的参考价值。
写小白天堂系列的文章算是从这一篇开始吧,但是写这个词法语法分析器实在是因为编译原理老师扣啊,哎,没办法,只能直接写代码,当时正好将javascript的语法基本撸了一边,所以就决定写一个JS的词法语法分析器,嗯,当然这个写哪种编程语法的分析器都一样,最多是在词法分析器中有点区别,他们的语法分析器几乎都是一样的,构造First集,Follow集,然后就是构建出预测分析表M基本就OK了,如果你还想增加Select集也可以,虽然这个东西可以不写,但是有些教科书上却讲了这个东西。
也许上面说的东西,有些读者不懂,俺懂滴,都是不听课的人呀,嘿嘿,放心,接下来让你秒懂这些玩意,believe me。
这里先提供个人代码中处理的两个类
class Grammer;
class Lex {
private:
class Lexical {
public :
string Lexname;//类型名称
int Lexcode;//类别编号
public :
Lexical(string Lexname, int Lexcode): Lexname(Lexname), Lexcode(Lexcode) {}
void toString() {
if(Lexcode >= OPERATOR_LIMIT_BASE) cout << "界限符";
else if(Lexcode >= OPERATOR_BASE) cout << "运算符";
else if(Lexcode >= CONSTANT_BASE) cout << "常量";
else if(Lexcode >= KEYWORD_BASE) cout << "保留字";
else cout << "标识符";
cout << " : (" << Lexname << " , " << Lexcode << ")" << endl;
}
string getLexTypename() {
if(Lexcode >= OPERATOR_LIMIT_BASE) return Lexname;
else if(Lexcode >= OPERATOR_BASE) return Lexname;
else if(Lexcode >= CONSTANT_BASE + 1) return "csdigits";
else if(Lexcode >= CONSTANT_BASE) return "csstring";
else if(Lexcode >= KEYWORD_BASE) return Lexname;
else return "id";
}
};
friend class Grammer;
typedef bool (Lex::*JudgeFunc)(int, bool);
const static int KEYWORD_BASE = 1000;//关键字基址
const static int KEYWORD_LEN = 21;//关键字种类个数
const static int CONSTANT_BASE = 10000;//常量基址
const static int CONSTANT_LEN = 3;//常量种类个数
const static int OPERATOR_BASE = 100000;//符号基址
const static int OPERATOR_LEN = 22;//符号种类个数
const static int OPERATOR_LIMIT_BASE = 1000000;//界限符基址
const static int OPERATOR_LIMIT_LEN = 11;//界限符种类个数
const static int VARIABLE_BASE = 0;//变量基址
const static string KeywordArr[KEYWORD_LEN];//保留字即关键字数组
const static string OperatorArr[OPERATOR_LEN];//运算符数组
const static string OperatorLimitArr[OPERATOR_LIMIT_LEN];//界限符数组
const static string ConstantArr[CONSTANT_LEN];//常量数组
JudgeFunc ConstantFuncArr[CONSTANT_LEN];//常量处理数组
map<string, int> KeyValueMap;//种类编码映射表
vector<Lexical> Lt;//词法结果数组
string curDealStr;//当前格式化后的字符串
int curPositionIndex;//当前处理常量的常量类型是整型还是浮点还是字符串
int curPositionLen;
public :
Lex();
inline void LexInit();//初始化数据
inline void SystemInit();
inline void TagInit();
inline void AnnoInit();
inline void KeywordInit();
inline void ConstantInit();
inline void OperatorInit();
inline void OperatorLimitInit();
void Scanner(string inStr);//分析字符串的构造出词法表
string StrCleanUp(string inStr);//去掉注释【此函数的代码随便写的不一定正确,所以请注意,如果发现代码问题,可以自己完成函数的功能】
bool JudgeVar(int, bool);//判断是否是标识符
bool JudgeInte(int, bool);//判断是否为整数常量
bool JudgeDec(int, bool);//判断是否为浮点常量
bool JudgeStr(int, bool);//判断是否为字符串常量
bool JudgeSym(int, bool);//判断是否为运算符
bool JudgeSymLimit(int, bool);//判断是否为界限符
void CycleDeal(int &, JudgeFunc, string);//根据情况调用上述的几个判断函数
inline void print();//输出词法分析的结果
inline pair<string, int> out();//啥都没用
};
const string Lex::KeywordArr[KEYWORD_LEN] = {
"var", "for", "return", "break", "continue", "function", "const", "let", "class", "extends", "if", "else", "else if", "while", "new", "import", "from", "in", "of", "null", "undefined"
};
const string Lex::OperatorArr[OPERATOR_LEN] = {
"++", "--", "+=", "-=", "^=", "&=", "+", "-", "*", "/", "=", "&", "^", ">", "<", ">=", "<=", "==", "~", "%", "||", "&&"
};
const string Lex::OperatorLimitArr[OPERATOR_LIMIT_LEN] = {
"(", ")", "[", "]", "{", "}", ",", ";", ".", ":", "#"
};
const string Lex::ConstantArr[CONSTANT_LEN] = {
"constantStr", "constantInte", "constantDec"
};
Lex::Lex() {
ConstantFuncArr[0] = &Lex::JudgeStr;
ConstantFuncArr[1] = &Lex::JudgeInte;
ConstantFuncArr[2] = &Lex::JudgeDec;
}
class Grammer {
private:
Lex CLex;
map<string, vector<string> > Grav;//最开始的语法集
map<string, set<string> > Firstv;//First集
map<string, bool> FirstvBool;//用于判断First集是否已经构造完成
// map<string, bool> FollowvBool;
bool FollowvNotAdd;//用于判断Follow集是否构造完成
bool FirstvNotAdd;
map<string, map<string, string> > anasiM;//预测分析表M
set<string> terminator;//终结符集
set<string> notTerminator;//非终结符集
vector<string> _stack;//栈符
map<string, set<string> > Followv;//Follow集
public:
Grammer();
inline void initLexProcessor(string);//初始化词法分析器
inline void initGrammerProcessor(string);//初始化语法分析器
void anaisGrammer(string);//分析语法
void anaisFirst();//分析First集
void dfsFirst(string, bool&);//递归处理First集
void anaisFollow();//分析Follow集
void dfsFollow(string);//处理Follow集,求Follow集的时候没有递归处理
void anaisAnaisM();//分析预测分析表M
void anaisProcesser();//分析程序
void createInputQueue();//这个函数暂时没有使用
void insertFirstv(string, string);
void insertFirstv(string, set<string>::iterator, set<string>::iterator);
void insertFollowv(string, string);
void insertFollowv(string, set<string>::iterator, set<string>::iterator);
void insertGrav(string, string);
inline void print();
void trim(string &);//去掉字符串开头和结尾的空格
void testprintGrav();
void testprintFirstv();
void testprintFollowv();
void testprintTerminator();
void testprintNotTerminator();
void testprintAnaisM();
void testprint_stack();
void testprint_Lt(int);
};
接下来开始开启小白世界,先说说词法分析器
词法分析器
这个分析器是最简单的,为什么呢,因为我们使用编程语法,右边就遇到几种类别的数据:
- 界限符
- 运算符
- 常量
- 保留字
- 标识符
最多你的常量可以细分为字符串常量和数字常量,而数字常量又可以细分为浮点型常量和整型常量,当然你还可惜细分,而我就分了上面的五种类别。
然后我们的代码直接分析就可以了,我的方法是直接保存这几种类型到相应的字符串数组中然后一一判断即可,比如我的数组是如此的:
const string Lex::KeywordArr[KEYWORD_LEN] = {
"var", "for", "return", "break", "continue", "function", "const", "let", "class", "extends", "if", "else", "else if", "while", "new", "import", "from", "in", "of", "null", "undefined"
};
const string Lex::OperatorArr[OPERATOR_LEN] = {
"++", "--", "+=", "-=", "^=", "&=", "+", "-", "*", "/", "=", "&", "^", ">", "<", ">=", "<=", "==", "~", "%", "||", "&&"
};
const string Lex::OperatorLimitArr[OPERATOR_LIMIT_LEN] = {
"(", ")", "[", "]", "{", "}", ",", ";", ".", ":", "#"
};
const string Lex::ConstantArr[CONSTANT_LEN] = {
"constantStr", "constantInte", "constantDec"
};
如果在Lex::KeywordArr中的话就是保留字,如果在Lex::OperatorArr就是运算符,Lex::OperatorLimitArr中就是界限符,Lex::ConstantArr中则是常量,如果不在这几个中的话就是标识符。
然后就是标识符是如何识别的呢,我想编译原理说的非常清楚了,不是数字和几个特殊字符开始的字符串就是标识符了,比如说_sdfds464(标识符), 4654(不是标识符)。
这个基本就是词法分析器了,这个东西大家随便写写就可以了,只是识别上面五种子串而已,这个就有点像我们平时C语言练习题,求一个单词在一段文章中是否存在一样,很简单。
重中之重,语法分析器,先不管为什么要构造First集和Follow集,先求出它们再说。
First集
编译原理书上是这么写的
Vt(终结符),Vn(非终结符),e(空集)
若
X属于Vt,则FIRST(X)={X};若
X属于Vn,且有产生式X->a..,则将终结符a加入FIRST(X)中,若X->e,则将终结符e加入FIRST(X)中;若
X->Y...是一个产生式且Y属于Vn,则把FIRST(Y)中的所有非e元素都加到FIRST(X)中,若X->Y1Y2...Yk是一个产生式,Y1,...,Yi-1是非终结符,而且,对于任何j,1<=j<=i-1,FIRST(Yj)都含有e,则把FIRST(Yi)中的所有非e元素都加到FIRST(X)中,特别是,若所有的FIRST(Yj)均含有e,j=1,2,...,k,则把e加到FIRST(X)中。
书上说的好像很叼的样子,大家如果仔细看也是很明白的,只是因为懒不想看,所以请看个人的超简单解析
首先明白什么是终结符,什么是非终结符,终结符就是无法转换下去的字符,比如说a如果在产生式中没有在->左边出现过就是终结符,如果有a->x...,那么a就不是终结符,而不是终结符就是非终结符。
如果
A是终结符则FIRST(A)={A}如果
A是非终结符,那么一定存在A->a...,就直接将a加入到FIRST(A)中,即便a是e如果
A是非终结符,存在A->abcd...y,如果FIRST(a)包含e,则要将FIRST(b)中除了e之外的元素加入到FIRST(A),递推下去,当FIRST(a)和FIRST(b)都包含e则将FIRST(c)中除了e之外的元素加入到FIRST(A),如果a到y的所有FIRST集都包含e则将e加入到FIRST(A)中。
然后是对上面的这几个步骤不断的处理,直到每一个FIRST集都不在增大为止退出构造。
伪代码来一波
while(true){
if(A是终结符) First[A] = {A};
if(A是非终结符){
//如果存在这个产生式A->abcd...
First[A].add(First[a].remove(e));
position p;//这个是指向abcd的指针
while(First(p).iscontains(e)){
p ++;
First[A].add(First(p).remove(e));
}
if(p已经指向A->abcd...最后一个终结符了){
First(A).add(e);
}
}
}实际代码过程中,我并没有执行第一种处理就是if(A是终结符) First[A] = {A};,而是只有A->a,而a是终结符才会执行这个判断,这样就导致了后面求FOLLOW和预测分析表的时候没有按照博客中写的形式,而是改变了一种方式,当然很明显,大家直接用上述的这些伪代码直接写是最好的。
真实代码
void Grammer::dfsFirst(string name, bool &_$) {
if(FirstvBool[name]) {//如果First集已经求过了,就直接返回,当然要判断当前集合是否包含e(空集)
if(Firstv[name].find("$") != Firstv[name].end()) _$ = true;
return ;
}
FirstvBool[name] = true;
auto e = Grav[name];
for(auto it = e.begin(); it != e.end(); it ++) {
string tmp = *it, tm = "", ztm = "";
trim(tmp);
bool tflag = false;
stringstream in(tmp);
while(in >> tm) {
if(tm[0] == '<' && tm[tm.length() - 1] == '>') {//非终结符的判断
dfsFirst(tm, _$);
insertFirstv(name, Firstv[tm].begin(), Firstv[tm].end());
tflag = true;
//如果当前First[tm]集包含e,则接着往下处理,否则不往下处理了
if(!_$) break;
}
if(!tflag) break;
}
in.clear();
in.str(tmp);
in >> tm;
if(tm[0] != '<' || tm[0] == '<' && tm[tm.length() - 1] != '>') {//终结符的判断
if(tm == "$") _$ = true;
else terminator.insert(tm);
insertFirstv(name, tm);//name->tm,tm是一个终结符
insertFirstv(tm, tm);//First[A] = {A}的情况
}
notTerminator.insert(name);
}
}
void Grammer::anaisFirst() {
for(auto it = Grav.begin(); it != Grav.end(); it ++) {
bool _$ = false;
dfsFirst(it -> first, _$);
}
}
FOLLOW集
编译原理书上是这么写的
对于文法的开始符号
S,置#于FOLLOW(S)中若
A->abc是一个产生式,则把FIRST(c)\\{e}加到FOLLOW(b)中若
A->abc是一个产生式或者FIRST(c)中存在e则将FOLLOW(A)加到FOLLOW(b);
个人的教科书对FOLLOW集的解释还是比较清晰的,这个和FIRST处理是一样的需要处理到,每一个FOLLOW集都不在增大为止退出构造。
这个就是不断循环了,编译原理书上讲的非常明白。
伪代码又一波
if(S是开始符号) FOLLOW(S).add("#");
while(从b开始往后处理){
则把FIRST(c)\\{e}加到FOLLOW(b)中
if(FIRST(c)包含e){
将FOLLOW(A)加入到FOLLOW(b)
}
}真实代码
void Grammer::dfsFollow(string name) {
auto e = Grav[name];
for(auto it = e.begin(); it != e.end(); it ++) {
string tmp = *it, otm, ntm;
trim(tmp);
int flag = 0;
stringstream in(tmp);
while(in >> ntm) {
flag ++;
if(flag > 1 && otm[0] == '<' && otm[otm.length() - 1] == '>') {
if(ntm[0] == '<' && ntm[ntm.length() - 1] == '>') {//针对非终结符
insertFollowv(otm, Firstv[ntm].begin(), Firstv[ntm].end());//则把FIRST(c)\\{e}加到FOLLOW(b)中
if(Firstv[ntm].find("$") != Firstv[ntm].end()) {
insertFollowv(otm, Followv[name].begin(), Followv[name].end());//将FOLLOW(A)加入到FOLLOW(b)
}
} else insertFollowv(otm, ntm), terminator.insert(ntm);//这里是针对终结符的
}
otm = ntm;
}
insertFollowv(otm, Followv[name].begin(), Followv[name].end());
}
}
void Grammer::anaisFollow() {
FollowvNotAdd = true;
insertFollowv("<程序起始点>","#"); //if(S是开始符号) FOLLOW(S).add("#");
while(FollowvNotAdd) {//这个和FIRST处理是一样的需要处理到,每一个FOLLOW集都不在增大为止退出构造。
FollowvNotAdd = false;
for(auto it = Grav.begin(); it != Grav.end(); it ++) {
dfsFollow(it -> first);
}
}
}预测分析表
M
这个表是在FIRST和FOLLOW的基础上来构造预测分析表M
书上
每一个终结符
a属于FIRST(A),把A->a加到M[A,a]中若
e属于FIRST(A),则对于任何b属于FOLLOW(A)把A->a加到M[A,b]
伪代码就不说了,很简单
这个第二点处理需要注意,比如说A->abcd,e属于FIRST(a),将A->a加到M[A,b],我们不能就此结束,而是要接着判断b,如果FIRST(b)包含e就接着处理c,如果FIRST(c)不包含e则退出第二种处理
构造的预测分析表M是非终结符为行,终结符为列
void Grammer::anaisAnaisM() {
terminator.insert("#");
string tmp = "", ntmp = "";
for(auto it = notTerminator.begin(); it != notTerminator.end(); it ++) {
for(auto jt = terminator.begin(); jt != terminator.end(); jt ++) {
anasiM[*it][*jt] = "";
}
}
for(auto it = notTerminator.begin(); it != notTerminator.end(); it ++) {
if(Firstv[*it].find("$") != Firstv[*it].end()) {//若e属于FIRST(A),则对于任何b属于FOLLOW(A)把A->a加到M[A,b]
for(auto et = Followv[*it].begin(); et != Followv[*it].end(); et ++) {
anasiM[*it][*et] = "$";
}
}
for(auto jt = terminator.begin(); jt != terminator.end(); jt ++) {
if(Firstv[*it].find(*jt) == Firstv[*it].end()) continue;
for(auto kt = Grav[*it].begin(); kt != Grav[*it].end(); kt ++) {
tmp = *kt, trim(tmp), ntmp = "";
int i = 0;
//每一个终结符a属于FIRST(A),把A->a加到M[A,a]中
/*
这个第二点处理需要注意,比如说A->abcd,e属于FIRST(a),将A->a加到M[A,b],
我们不能就此结束,而是要接着判断b,
如果FIRST(b)包含e就接着处理c,如果FIRST(c)不包含e则退出第二种处理
*/
do {
ntmp = "";
bool flag = false;
for(; i < tmp.length(); i ++) {
if(tmp[i] == ' ' && flag) break;
if(tmp[i] == ' ') continue;
ntmp += tmp[i];
flag = true;
}
} while(i < tmp.length() && Firstv[ntmp].find(*jt) == Firstv[ntmp].end() && Firstv[ntmp].find("$") != Firstv[ntmp].end());
if(Firstv[ntmp].find(*jt) != Firstv[ntmp].end()) {
anasiM[*it][*jt] = *kt;
break;
}
}
}
}
}最终程序判断
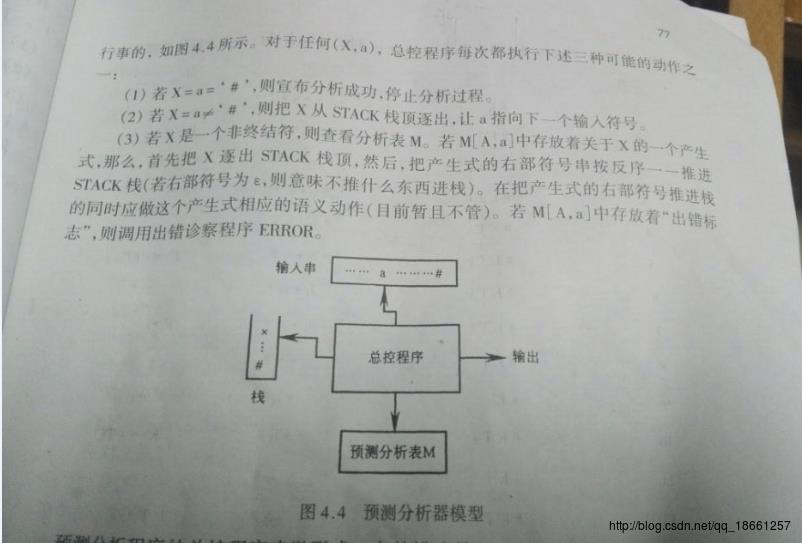
这个东西跟书上的运用栈处理是一样的,这里就不多讲了。
wf.txt文法文件(针对js但是不完整)
<程序起始点> -> <程序闭包>
<程序闭包> -> <函数块闭包> | $
<声明> -> <类型> <变量> <赋初值>
<操作变量> -> <标志符> <对象操作>
<对象操作> -> <数组下标> | . <标志符> | $
<变量> -> <标志符> <数组下标>
<标志符> -> id
<类型> -> var | const | let
<数组下标> -> [ <因式> ] | $
<因式> -> ( <表达式> ) | <操作变量> | <数字>
<数字> -> csdigits
<表达式> -> <因子> <项>
<因子> -> <因式> <因式递归>
<因式递归> -> * <因式> <因式递归> | / <因式> <因式递归> | $
<项> -> + <因子> <项> | - <因子> <项> | $
<赋初值> -> = <右值> | $
<右值> -> <表达式> | <字符串> | [ <数组闭包> ] | { <多个数据> } | <函数调用> | <函数定义>
<函数名> -> <标志符>
<多个数据> -> <对象数据> <对象闭包> | $
<对象闭包> -> , <对象数据> <对象闭包> | $
<对象数据内容> -> <字符串> | <数字> | [ <数组闭包> ] | null | { <多个数据> }
<对象数据> -> <字符串> : <对象数据内容> | <标志符> : <对象数据内容>
<数组闭包> -> <对象数据内容> <数组递归> | $
<数组递归> -> , <数组元素> <数组递归> | $
<字符串> -> csstring
<函数定义> -> function <函数声明>
<函数声明> -> <非匿名函数声明> | <匿名函数声明>
<非匿名函数声明> -> <函数名> ( <参数声明> ) { <函数块> }
<匿名函数声明> -> ( <参数声明> ) { <函数块> }
<参数声明> -> id <参数声明闭包> | $
<参数声明闭包> -> , id <参数声明闭包> | $
<声明语句闭包> -> <声明语句> <声明语句闭包> | $
<声明语句> -> <声明> ;
<函数块> -> <声明语句闭包> <函数块闭包>
<函数体> -> <执行操作> | <for循环> | <条件语句> | <函数返回> | <函数定义>
<函数块闭包> -> <函数体> <函数块闭包> | $
<执行操作> -> <执行体> ;
<执行体> -> <声明> | <后缀表达式> | $
<函数调用> -> . <函数名> ( <参数列表> ) <函数链接调用>
<函数链接调用> -> . <函数名> ( <参数列表> ) <函数链接调用> | $
<赋值操作> -> <操作变量> <赋值或函数调用> | <声明> ; | $
<赋值或函数调用> -> = <右值> ; | <函数调用>
<参数列表> -> <参数> <参数闭包>
<参数闭包> -> , <参数> <参数闭包> | $
<参数> -> <标志符> | <数字> | <字符串> | <函数定义>
<for循环> -> for ( <赋值操作> <逻辑表达式> ; <后缀表达式> ) { <函数块> }
<后缀表达式> -> <操作变量> <后缀运算符> | $
<后缀运算符> -> ++ | -- | <多重运算符> <右值> | ( <参数列表> ) <函数链接调用>
<多重运算符> -> += | -= | *= | &= | /=
<逻辑表达式> -> <表达式> <逻辑表达式闭包> | $
<逻辑表达式闭包> -> <逻辑运算符> <表达式> <逻辑表达式闭包> | $
<逻辑运算符> -> < | > | == | === | != | !== | <= | >= | && | || | |= | ^=
<条件语句> -> if ( <逻辑表达式> ) { <函数块> } <否则语句>
<否则语句> -> else <否则扩展语句> | $
<否则扩展语句> -> <条件语句> | { <函数块> }
<函数返回> -> return <返回值> ;
<返回值> -> <表达式> | $测试程序
_("abc").click(function(){
var a = "abc";
}).focus(function(a, b){
return a + b;
}).on(function(){
if(1){
console.log("abc");
}
else if(2){
console.log("abc");
}
});
总代码
#include <map>
#include <set>
#include <stack>
#include <cstdio>
#include <string>
#include <vector>
#include <sstream>