斐波拉契数列的计算方法

Posted 2020-09-18 秋天的竹子

用非递归方法计算斐波那契数列，节省时间，包括迭代法，中间变量保存法，公式法

面试题9、斐波拉契数列

题目：

输入整数n，求斐波拉契数列第n个数。

思路：

一、递归式算法：

利用f(n) = f(n-1) + f(n-2)的特性来进行递归，代码如下：

代码：

long long Fib(unsigned int n)
{
    if(n<=0)
        return 0;
    if(n==1)
        return 1;
    return Fib(n-1) + Fib(n-2);
}

缺陷：

当n比较大时递归非常慢，因为递归过程中存在很多重复计算。

二、改进思路：

应该采用非递归算法，保存之前的计算结果，用空间换时间。

代码如下：

#include<stdio.h>
#include<stdlib.h>
using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    int num1 = 0;
    int num2 = 1;
    for(int i=2;i<n;i++)
    {
        int tmp = num1 + num2;
        num1 = num2;
        num2 = tmp;
    }
    printf("%d", num2);
}

相似题目：

1、青蛙跳台阶，一次可以跳1或者2格，共n阶台阶，问有多少种上台阶的方法？

思路：从后往前想，f(n) = f(n-1) + f(n-2)，转换成同样的题目了。

2、矩形覆盖问题，用21的矩形来覆盖28的矩形，小矩形可以横着或竖着来覆盖，问有多少种方法去覆盖？

思路：横着覆盖就变成了f(8) = 1+f(8-2)，竖着变成f(8) = 1 + f(8-1)，所以f(8) = f(8-1) + f(8-2)。

转载来源：http://www.cnblogs.com/puyangsky/p/5826466.html

---

 

题目要求：

　　写一个函数，输入n，求斐波拉契数列的第n项。斐波拉契数列的定义如下：

　　

　　参考资料：剑指offer第9题、编程之美2.9

题目分析：

　　方法1：递归法，效率很低，而且会计算很多重复；

#include <stdio.h>

#define uint64 unsigned __int64 

uint64 Fibonacci(int n);

int main(void)
{
    int n;

    while(1)
    {
        printf("请输入n值：");
        scanf("%d",&n);

        printf("n = %d,Fibonacci(n) = %I64u\\n",n,Fibonacci(n));    
    }    
    return 0;
}
uint64 Fibonacci(int n)
{
    if(n <= 0)
        return 0;
    else if(n == 1)
        return 1;
    else
        return (Fibonacci(n-1)+Fibonacci(n-2));
}

　　方法2：迭代法，通过保存中间项避免重复计算，时间复杂度O(n);

#include <stdio.h>
#include <assert.h>

int main(void)
{
    int n,i = 0;
    int x,y;

    while(1)
    {
        printf("请输入n值：");
        scanf("%d",&n);
        assert((n >= 0) && (n <= 92));//用这种方法的n最大为92，否则就溢出了。

        i = 0;
        x = 0;
        y = 1;
        while(i < n)
        {
            y = x+y;
            x = y-x;
            i++;
        }
        if(n <= 0)
            y = x;
        printf("n = %d,Fibonacci(n) = %d\\n",n,y);

    }    
    return 0;
}

　　方法3：公式法，时间复杂度O(1),因为公式中引入了无理数，所以不能保证结果的精度；

#include <stdio.h>
#include <assert.h>
#include <math.h>

double Pow(double x,unsigned int n);

int main(void)
{
    int n;
    int fibo;
    double a,b,c;
    a = sqrt(5.0);
    b = (1+a)/2;
    c = (1-a)/2;
    while(1)
    {
        printf("请输入n值：");
        scanf("%d",&n);
        assert((n >= 0));
        
        int x = pow(b,n);
        int y = pow(c,n);
        fibo = (int)(a*(Pow(b,n)-Pow(c,n))/5);
        printf("n = %d,fibonacci(n) = %d\\n",n,fibo);
    }    
    return 0;
}
double Pow(double x,unsigned int n)
{
    double result = 1;
    while(n)
    {
        if(n & 0x01)
            result *= x;
        x  = x*x;
        n >>= 1;
    }
    return result;
}

　　方法4：分治策略，可以用矩阵来表示,则,(这个式子是通过计算A、A²、A³、、、观察出来的)其中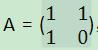，则上面这个式子可以表示为：

则F₂ = Y2_11 = A（11表示矩阵的第1行1列元素）.

　　　　　现在剩下的问题就是求Aⁿ了，可以把n用二进制表示：n = ak*2^k + ak-1*2^k-1 + ... + a1*2 + a0，其中ai = 0 或1 ，i = 0,1,2... k。例如：n = 5 = b’101 = 1*2² + 0*2¹+1*2⁰。这样

则，我们知道Aⁿ最多经过log₂n乘法就能够得到，而不用A*A*A这样计算n次。

代码实现：

　

#include <stdio.h>
#include <assert.h>

const int MAXLENGTH = 10;

struct Matrix 
{
    unsigned side;
    __int64 dat[MAXLENGTH*MAXLENGTH];//也可以用行/列来表示(row、line)，会更方便一点。
};

// 方阵的乘法 
void MatrixMult(const Matrix a, const Matrix b, Matrix &m)
{
    unsigned int i,j,k;
    assert(a.side == b.side);
    m.side = a.side;
    for (i=0; i < m.side; ++i)
        for (j=0; j < m.side; ++j)
        {
            m.dat[i*m.side+j] = 0;
            for (k=0; k<m.side; ++k)
                m.dat[i*m.side+j] += a.dat[i*a.side+k]*b.dat[k*b.side+j];
        }
}

__int64 Fibonaci(unsigned n)
{
    if (n==0) 
        return 0;

    --n;    // 计算矩阵prod的n-1次幂

    Matrix res;    
    res.side = 2;
    res.dat[0] = 1; res.dat[1] = 0; 
    res.dat[2] = 0; res.dat[3] = 1;

    Matrix prod;        
    prod.side = 2;
    prod.dat[0] = 1;  prod.dat[1] = 1;
    prod.dat[2] = 1;  prod.dat[3] = 0;

    // 只需要O(logn)的复杂度就能算出x的n次幂  
    while (n)
    {
        // 如果n的最低二进制位为1，则乘上对应的幂次prod
        if (n&1) MatrixMult(res, prod, res);
        MatrixMult(prod, prod, prod);
        n >>= 1;
    }
    return res.dat[0];
}

int main(void)
{
    int i;

    for(i = 0;i < 20;i++)
    {
        printf("%I64u\\n",Fibonaci(i));
    }
    
    return 0;
}

转载来源：http://www.cnblogs.com/tractorman/p/4058305.html