求解魔术矩阵问题！

Posted 2023-04-26

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
void main()

int array[16][16]=0,i,j,k,n=5;
/*初始化*/
//为什么这里一定要先初始化为0，而且 i要等于n+1才能使用呢
for(i=1;i<=n;i++)
for(j=1;j <=n;j++)
array[i][j]=0;
/*建立魔方矩阵*/

j=(n/2)+1;
array[1][j]=1;
for(k=2;k <=n*n;k++)

i=i-1;
j=j+1;
if((i <1)&&(j> n))

i=i+2; //这里为什么是 i=i+2；
j=j-1;

else

if(i <1)
i=n;
if(j> n)
j=1;

if(array[i][j]==0)
array[i][j]=k;
else

i=i+2; //还有这里为什么也是 i=i+2；
j=j-1;
array[i][j]=k;



/*输出n阶魔方矩阵*/
for(i=1;i <=n;i++)

for(j=1;j <=n;j++)
printf( "%5d ",array[i][j]);
printf( "\n\n ");



对平面魔方的构造，分为三种情况：N为奇数、N为4的倍数、N为其它偶数(4n+2的形式) ⑴ N 为奇数时，最简单 (1) 将1放在第一行中间一列; (2) 从2开始直到n×n止各数依次按下列规则存放： 每一个数存放的行比前一个数的行数减1，列数加1 (3) 如果行列范围超出矩阵范围，则回绕。 例如1在第1行，则2应放在最下一行，列数同样加1; (4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时， 则把下一个数放在上一个数的下面。

⑴ N 为奇数时，最简单
(1) 将1放在第一行中间一列;
(2) 从2开始直到n×n止各数依次按下列规则存放：
按 45°方向行走，如向右上
每一个数存放的行比前一个数的行数减1，列数加1
(3) 如果行列范围超出矩阵范围，则回绕。
例如1在第1行，则2应放在最下一行，列数同样加1;
(4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时，
则把下一个数放在上一个数的下面。

17 24 1 8 15

23 5 7 14 16

4 6 13 20 22

10 12 19 21 3

11 18 25 2 9

可以不初始化 因为这个数组int array[16][16]=0；已经对其初始化赋值为0； i也可以等于是1，因为初始位置是第一行中间，所以i=1,j=(n/2)+1
如果i=n+1 和i=1 结果是一样的
i=1时 i=i-1后i==0，然后经过 if(i <1) i=n; ，i==n
i=n时 i=i-1后i==n
后面的i-2是因为
(4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时，
则把下一个数放在上一个数的下面。
要把数放在上一个数下面就要i++;但是前面已经i=i-1 j=j+1了所以要i=i+2 j=j-1 参考技术A 都得0是为了初始化，因为你取得这个数组的元素是未知的，如果有的元素没有变化，则他是个未知数，可以很大，可以很小。
i+2，不明白，不知道魔术矩阵个什么东东

矩阵乘法：分析问题，确定递推式，采用矩阵快速幂求解

      应用矩阵快速幂运算可以解决递推问题。在实际应用中，有时候题目并没有直接给出递推式，需要认真分析问题，找出递推式，然后再利用矩阵快速幂运算加快问题的求解。

【例1】程序阅读理解。

      有如下的C语言程序：

#include <stdio.h>
int main()

     int n,m,f,i;
     while(scanf("%d%d",&n,&m)!=EOF)
     
           f=0;
           for(i=1;i<=n;i++)
           
                if (i&1)f=(f*2+1)%m;
                else f=f*2%m;
           
           printf("%d\\n",f);
     
     return 0;

       阅读上面的程序，根据输入的n和m，写出程序运行的结果。例如，输入 3  10，输出应为5。

       但由于给定输入的n和m的数据范围为1<=n, m <= 1000000000，且测试集中数据量较大，因此如果直接将给定的程序提交会超时的。请你编写一个程序，能根据输入的n和m快速完成问题的求解，以实现给定程序的功能。

      （1）编程思路。

      给定程序段实际是通过迭代的方式求f(n)%m的值。先不考虑求余，找到f(n)的求法。

      分析给定程序知，f(0)=0， 当 n为奇数时，f(n)=2*f(n-1)+1；当n为偶数时，f(n)=2*f(n-1)。

      下面进一步分析，找到不考虑n的奇偶性的一个统一的递推式。

       当 n为奇数时，f(n)=2*f(n-1)+1，n-1一定为偶数，f(n-1)=2*f(n-2)。因此，

                f(n)=f(n-1)+f(n-1)+1=2*f(n-2)+f(n-1)+1。

       当 n为偶数时，f(n)=2*f(n-1)，n-1一定为奇数，f(n-1)=2*f(n-2)+1。因此，

                f(n)=f(n-1)+f(n-1)=2*f(n-2)+f(n-1)+1。

      由此，得到统一的递推式： f(0)=0，f(1)=1，  f(n)=2*f(n-2)+f(n-1)+1  (n>=3)。

      确定了递推式后，可以构造矩阵P，进行快速幂运算求解。

       

      

 

      

 

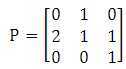
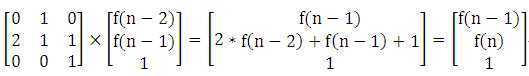
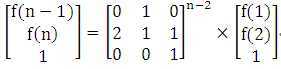
       （2）源程序。

#include <stdio.h>
#include <string.h>
struct Matrix

      __int64 mat[4][4]; // 存储矩阵中各元素
;
Matrix matMul(Matrix a ,Matrix b,int n,int m)

      Matrix c;
      memset(c.mat,0,sizeof(c.mat));
      int i,j,k;
      for (k = 1; k<=n ; k++)
          for (i=1 ;i<=n ; i++)
              if (a.mat[i][k]!=0)
                  for (j = 1 ;j<=n ;j++)
                      c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % m;
      return c;

Matrix quickMatPow(Matrix a ,int n,int b,int m) // n阶矩阵a快速b次幂

      Matrix c;
      memset(c.mat ,0 ,sizeof(c.mat));
      int i;
      for (i = 1 ;i <= n ;i++)
           c.mat[i][i] = 1;
      while (b!=0)
     
           if (b & 1)
               c = matMul(c ,a ,n,m); // c=c*a;
           a = matMul(a ,a ,n,m); // a=a*a
           b /= 2;
     
      return c;

int main()

      int n,m;
      __int64 ans;
      Matrix p;
      while(scanf("%d%d" ,&n,&m)!=EOF)
     
            memset(p.mat,0,sizeof(p.mat));
            p.mat[2][1]=2;
            p.mat[1][2]=p.mat[2][2]=1;
            p.mat[2][3]=p.mat[3][3]=1;
            if (n<3)
                 printf("%d\\n",n%m);
           else
           
                 p = quickMatPow(p,3,n-2,m);
                 ans=p.mat[2][1]% m;
                 ans=(ans+p.mat[2][2]*2)% m;
                 ans=(ans+p.mat[2][3])% m;
                 printf("%I64d\\n" ,ans);
         
     
      return 0;

【例2】将灯全熄灭。

       有n个灯排成一行，初始时是全亮的，第一个灯可以按（按下之后改变状态）。然后如果前k个灯全熄灭且第k+1个灯亮，则第k+2个灯可以按。问至少要多少步灭掉所有灯？

      例如，n=2时，需要2歩。第1歩灭掉2号灯，第2歩灭掉1号灯。n=3时，需要5歩。第1歩灭掉1号灯，第2歩灭掉3号灯，第3歩点亮1号灯（注意1号灯不点亮，不能直接灭2号灯），第4歩灭掉2号灯，第5歩灭掉1号灯。

      （1）编程思路。 

       设f[n]代表n个全亮的灯变成全熄灭所需的最少步数，也可以代表n个全熄灭的灯变成全点亮所需的最少步数。 
      1）要想灭掉最后一个灯，得先灭掉前n-2个灯（第n-1个灯留亮），需要步数 f[n-2]+1。 
      2）要想灭掉第n-1个灯，得先让第n-2个灯变回亮，要第n-2个灯变回亮，得先让第n-3个灯变回亮...即要把前n-2个灯都变回亮，需要步数 f[n-2]。 
      3）把前n-2个灯变回亮后，就剩下前n-1个灯都是亮的，即剩下的任务就是把n-1个灯灭掉，需要步数 f[n-1]。 
      综上所述：f[n] = 2*f[n-2] + f[n-1] + 1。 （n>=3）  f[1]=1，f[2]=2。

      （2）源程序。

#include <stdio.h>
#include <string.h>
#define MOD 200907
struct Matrix

       __int64 mat[4][4]; // 存储矩阵中各元素
;
Matrix matMul(Matrix a ,Matrix b,int n)

      Matrix c;
      memset(c.mat,0,sizeof(c.mat));
      int i,j,k;
      for (k = 1; k<=n ; k++)
          for (i=1 ;i<=n ; i++)
              if (a.mat[i][k]!=0)
                  for (j = 1 ;j<=n ;j++)
                      c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % MOD;
      return c;

Matrix quickMatPow(Matrix a ,int n,int b) // n阶矩阵a快速b次幂

      Matrix c;
      memset(c.mat ,0 ,sizeof(c.mat));
      int i;
      for (i = 1 ;i <= n ;i++)
            c.mat[i][i] = 1;
      while (b!=0)
     
           if (b & 1)
                c = matMul(c ,a ,n); // c=c*a;
           a = matMul(a ,a ,n); // a=a*a
           b /= 2;
     
      return c;

int main()

      int n;
      __int64 ans;
      Matrix p;
      while(scanf("%d" ,&n) && n!=0)
     
           memset(p.mat,0,sizeof(p.mat));
           p.mat[1][2]=2;
           p.mat[1][1]=p.mat[1][3]=1;
           p.mat[2][1]=p.mat[3][3]=1;
           if (n<3)
               printf("%d\\n",n%MOD);
           else
           
                p = quickMatPow(p,3,n-2);
                ans=(p.mat[1][1]*2+p.mat[1][2]+p.mat[1][3])%MOD;
                printf("%I64d\\n" ,ans);
           
     
      return 0;