感知机
Posted gaoshoufenmu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了感知机相关的知识,希望对你有一定的参考价值。
模型
机器学习中,感知机(perceptron)是一种二值的监督学习的算法(相应的函数,能决定输入是否属于某个分类,其中输入由一个数值向量表示)。感知机是一个线性分类器,其分类函数基于线性预测函数对新的输入作出预测,即,将输入(实数向量)映射到{-1,1}二值空间:
f(x)=sign(wx+b)
其中,sign是符号函数

wx是w向量与x向量的内积,w向量与x向量均为n维,分别为如下形式
w=[w1,w2,...,wn]
x=[x1,x2,...,xn]T
(也许会疑问,怎么知道f(x)就是这种形式的呢? ... 因为感知机就是定义为线性分类,自然分类函数f(x)就可以写成上面那种形式,当然对于数据集可以采用其他非线性分类的方法,不过这就不是这里的感知机的工作了 -_-!!)
不难发现,f(x)是n+1维欧氏空间的超平面,n维空间中的点被f(x)分为两部分(即两类),为了方便计算和表示,我们增加一个维度,使得b = w0x0, 其中x0=1,并且将w也写成列向量形式,则有,

其中,w=[w0,w1,w2,...,wn]T
感知机学习的目的就是要找到一个perceptron,能把不同类别的点区分开来,具体来说就是,由训练数据集
T={(x1,y1), (x2,y2), ... , (xN, yN)}
其中N表示有N个数据,xi属于n+1维实数空间向量,yi属于{1, -1},求n+1维向量w
当然,这里需要有一个前提条件,训练数据要线性可分(比如如下图中的数据就不能线性可分)
 (n+1=3,假设圈圈表示y值为1,叉叉表示y值为-1,图中三点一线,线性不可分)
(n+1=3,假设圈圈表示y值为1,叉叉表示y值为-1,图中三点一线,线性不可分)
线性可分是指:
如果存在某个超平面wTx=0,对数据集中所有yi=1的数据,wTxi>0,对所有yi=-1的数据,wTxi<0,则这个数据集线性可分
学习策略
定义(经验)损失函数(参数为w),并设法将损失函数极小化,比如损失函数为误分类点的个数,然后极小化为0,则就是找到一个符合要求的超平面。巴特,这样的损失函数不是关于w连续可导,不容易找。
如果选择损失函数为误分类点到超平面的总距离,那么当误分类点为0时,总距离也为0,分类正确。
输入空间一点x到超平面的距离为

其中,||w||为w的L2范数,然后,对于误分类点来说,距离则为

因为对于误分类点,y值与wTx符号相反,所以需要加个负号,股损失函数为误分类点总距离,假设误分类点集合为SetM,则,

对于上式右边括号中的部分,我们可以认为分母是为了让wT归一化,而我们目的也是为了让SetM最终为空集合,从而使L为0,所以这里分母并没有什么影响,为了简单起见,这里将分母去掉,
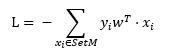
其中,SetM是误分类点集合,xi为n+1维列向量,w为n+1维列向量,yi为{1,-1}中的某个标量值,可以看出,误分类点越少,L越小,误分类点离超平面越近,L越小。当SetM为空集合(没有误分类点)时,L = 0,存在
误分类点时,在误分类点一定的情况下,L是w的线性函数。
学习算法
采用随机梯度下降法,这是因为只有误分类的点参与优化w,优化过程中,一次选择一个误分类点使其梯度下降。
损失函数对w的偏导数为

这是一个与xi一样的n维列向量,则针对某一个误分类点的梯度下降的优化为,
w← w + ayixi (*)
其中 + 号表示梯度下降,a表示步长,范围为(0,1],yi为第i个点的分类值(1,或者-1)。
还记得前面说的那个超平面的截距b吗?b其实就是这里的w0,因为x0=1,故
b←b + ayixi0 = b + ayi
当然了,这里b作为w的第0个分量,在计算表达式时没必要单独列出来优化。
算法:
1. 原始形式
输入:训练数据集{(x1,y1), (x2,y2), ... , (xN, yN)},对某个数据点(xi,yi),检测条件 yiwTxi > 0 是否满足,如果不满足表示是误分类点,则进行优化
输出:w 值
- 选择w初值,比如n+1维零向量[0,0, ... , 0]T ,,步长a选择1
- 遍历训练集:
a) 当(xi, yi), yiwTxi <= 0,则使用上面的(*)式对w进行优化,注意,xi的第0维值始终为1
b) 如果优化后依然yiwTxi <= 0,则继续a)步骤,直到 yiwTxi >0, 设置标志位flag 为true,表示有误差点
- 继续check (xi+1,yi+1), 如果不满足检测条件,则跳到2.a)步骤进行优化,否则继续检测 i + 2 的数据点。如此一直到训练集遍历结束
- 检测flag是否为true,如果为true,则 重置标志位为false,并跳至2步骤执行,否则退出
由于实际应用中,往往训练数据的x 是n维,可以视情况决定是否将b 独立出来优化计算。
2. 对偶形式
根据上面的(*)式,我们知道在最后计算完成后,w变为

(上式中i从i=1开始)其中ni为第i个数据总共参与优化的次数,如果将截距b单独写出来(对任意的xi,其第0维值为1),则b为:

可以假设w初值为零向量,则w可写为
 (1)
(1)
(上式中i从i=1开始)对应的b则为

其中xi为第i个数据点(n+1维列向量),yi为第i个数据点的分类值(1或者-1),a为步长(标量),ni为整个优化过程中,使用第i个数据点进行优化的次数
根据上面对原始形式的分析,我们知道,优化是检测每一个数据点是否符合检测条件 yiwTxi > 0, 带入w的表达式,检测条件变为:
 (2)
(2)
其中j表示N个数据集中第j个数据,xjTxi为向量内积,可以在一开始的时候计算,这样就得到一个所有内积的N*N的矩阵,这个就是Gram矩阵,从而避免在后面每一次循环的时候都要计算,从而节省时间,这也是对偶形式对原始形式所做的改进(原始形式中每次循环中wTxi就是做内积计算)。
总结步骤如下:
- 选择步长a为1,nj均为0
- 遍历训练集,
a) 当(xi, yi),不满足检测条件,则作优化,ni ← (ni+1)a = ni + 1,并设置标志位flag = true,表示此轮有误分类点
b) 然后重新检测条件是否满足,如不满足,跳至 a) 继续优化,否则跳到步骤3 - 检测下一个数据点(xi+1,yi+1) 是否满足条件,如不满足,跳至 2.a) 步骤,否则跳至 步骤4
- 检测标志位,如果为true,则reset flag = false,并跳至步骤2,否则,退出
需要注意的是,上面计算矩阵时,向量的内积是n+1维的,其中第0维值为定值1,这就导致Gram矩阵中每个元素值比n维时大1(注意,维度不变,仍然是N*N),这是为了方便表达才写成n+1维,如果实际计算中不方便这么处理,可以写成n维,那么检测条件变为

优化时,ni ← (ni+1)a = ni + 1,而 b ← (ni+1)yi,可以看出对所有N个数据点累加b的变化正好符合上面给出的式子。
补充说明
下面稍微证明一下优化是有效的,而不是碰运气。
假设wf是能够满足要求的,也就是说,对于数据集中任意一个数据点(xi,yi),都满足上面的检测条件yiwfTxi > 0,那么最小值也大于0, min(ywfTx) > 0,因为w是向量,所有如果当前的w与wf的夹角变小,说明优化是有效的
对于某一次使用数据点(xi,yi)优化后,wt 变成了wt+1,计算向量的内积
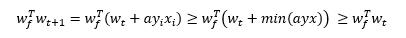
但是内积增大,不一定是说夹角变小,也许是wt+1的长度变大了呢?
考虑w的L2范数的平方(平方是为了计算方便)

注意上式中第一行最右端的第二项值小于等于0,这是因为使用的误差点不满足检测条件。
在给定训练数据集和步长a之后,上式第二行最右边的max(..)子项值是固定的,也就是说优化w,就算使其长度增加,也是有上限的。
现在,假设一开始w初值为0向量w0,经过t次优化为变成wt,那么,

且有

故而wt与wf的夹角余弦为,
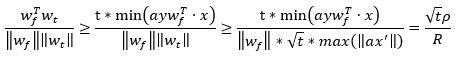
其中,
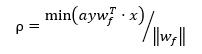
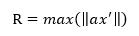
易知,这两个参数在给定步长a和数据集的情况下均为定值且大于0,注意到,因为wf下,所有数据点均符合检测条件,
所以ρ >0,且其中 wf被分母归一化,假设归一化后的wf为wfs,则wfs的为n+1维空间的单位向量,
而R 自然是大于0,因为不可能数据集中所有点均为零向量。
因为夹角余弦不超过1,所以
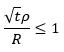
从而
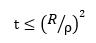
即,需要优化的步骤数t的上限。
Pocket Step
有时候数据集数量N特别大,或者数据集不是线性可分但是事先我们并不知道,这种时候导致优化将会消费大量时间,或者无法停止。这时,我们可以加入pocket step,也就是每次迭代优化w后,
重新使用原始数据集计算误分类次数(此时每次计算时不对w进行优化),并记录此次优化后的误分类次数,然后再对下一个数据点检测,并在需要的时候做优化,每次做完优化后就对原始数据集
统计误分类次数,当迭代优化T次后,就有对应的T个误分类次数,选择误分类次数最少的那个w。当N足够大的时候,所得到的w还算差强人意。
ref:
- 《统计学习方法》,李航
- http://beader.me/2013/12/21/perceptron-learning-algorithm/
示例代码
(仅作帮助理解用,未经测试)
感知机类
public class Perceptron { /// <summary> /// 第一项为b,对应的x0为1 /// </summary> public double[] w; /// <summary> /// 学习 /// </summary> /// <param name="data"></param> public void Learn(PData data) { w = new double[data.J]; var a = 1; // 这里简单起见,hardcode步长 bool flag = true; // 优化标志位,初始化为true while(flag) { flag = false; // 标志位复位 for(int i = 0; i < data.matrix.GetLength(0); i++) { var row = data.matrix[i]; // 一行表示一条数据 var dist = PUtil.CalcDistance(row, w); while(dist <= 0) { flag = true; // 表示进行过优化 PUtil.Calibrate(w, row, a); dist = PUtil.CalcDistance(row, w); } } } } /// <summary> /// 根据输入判断输出,输出为-1或1 /// </summary> /// <param name="input"></param> /// <returns></returns> public double Judge(double[] input) { double sum = 0; for(int i = 0; i < w.Length; i++) { if (i == 0) sum += w[i]; else sum += w[i] * input[i - 1]; } return sum >= 0 ? 1 : -1; } }
帮助类
public class PUtil { /// <summary> /// 计算点与超平面距离 /// </summary> /// <param name="row">数据点</param> /// <param name="w"></param> /// <returns></returns> public static double CalcDistance(double[] row, double[] w) { var y = row[row.Length - 1]; double sum = 0; for(int i = 0; i < w.Length; i++) { if (i == 0) sum += w[0]; else sum += w[i] * row[i - 1]; } return y * sum; } /// <summary> /// 校正 /// </summary> /// <param name="w">权重</param> /// <param name="row">数据点</param> /// <param name="a">步长</param> public static void Calibrate(double[] w, double[] row, double a) { var f = row[row.Length - 1] * a; for(int i = 0; i < w.Length; i++) { if (i == 0) w[i] += f; else w[i] += row[i - 1]; } } }
如果采用对偶形式的学习策略,则上面Learn方法修改为
/// <summary> /// 对偶形式的学习 /// </summary> /// <param name="data"></param> public void Learn_(PData data) { w = new double[data.J]; // 截距 b 作为 w的第一项 var N = data.matrix.GetLength(0); // 数据量 var gram = PUtil.GetGram(data.matrix); // 数据点输入的对偶内积矩阵 var n = new int[N]; // 每个数据点参与优化的次数 double a = 1; // 步长,hardcode 设置为 1 bool flag = true; while(flag) { flag = false; // 遍历数据点 for(int i = 0; i < N; i++) { var check = PUtil.Check_(data.matrix, i, gram, n, a); while(check < 0) { flag = true; // 本轮进行了优化 n[i] += 1; // 第 i 个数据点参与优化次数增 1 check = PUtil.Check_(data.matrix, i, gram, n, a); } } } // 设置 w 的值, 根据(1)式 for(int j = 0; j < data.J; j ++) { for(int k = 0; k < N; k++) { if (j == 0) w[j] += n[k] * a * data.matrix[k][data.J - 1]; else w[j] += n[k] * a * data.matrix[k][data.J - 1] * data.matrix[k][j - 1]; } } }
对应的辅助方法为
/// <summary> /// 获取数据输入的对偶内积矩阵 /// </summary> /// <param name="matrix"></param> /// <returns></returns> public static double[][] GetGram(double[][] matrix) { var N = matrix.GetLength(0); var J = matrix.GetLength(1); var gram = new double[N][]; for(int i = 0; i < N; i++) { gram[i] = new double[N]; for(int k = 0; k < N; k++) { double sum = 0; for(int j = 0; j < J; j++) { if (j == 0) sum += 1; else sum += matrix[i][j - 1] * matrix[k][j - 1]; } gram[i][k] = sum; } } return gram; } /// <summary> /// 对偶形式的检测条件 /// </summary> /// <param name="matrix"></param> /// <param name="i"></param> /// <param name="gram"></param> /// <param name="n"></param> /// <param name="a"></param> /// <returns></returns> public static double Check_(double[][] matrix, int i, double[][] gram, int[] n, double a) { var N = matrix.GetLength(0); // 样本数据量 var J = matrix.GetLength(1); // 数据维度 var xy = matrix[i]; // 当前检测的数据点 var multiply = gram[i]; // 关联 i 数据点的 内积向量 double sigma = 0; for(int k = 0; k < N; k++) { sigma += n[k] * a * matrix[k][J - 1] * multiply[k]; // (2)式 } return matrix[i][J - 1] * sigma; }
以上是关于感知机的主要内容,如果未能解决你的问题,请参考以下文章
DL之Perceptron:感知器(多层感知机/人工神经元)的原理之基于numpy定义2层感知机底层逻辑代码(与门AND/与非门NAND/或门OR是)解决XOR异或问题之详细攻略