求有向图的强连通分量的算法

Posted 2020-09-17 大神笨蛋

下面是求有向图的强连通分量的算法的代码：

import java.util.Scanner;
class Qiufenliang//定义求强连通分量的类
{
    String lu="";//定义的一个字符型变量，记录强连通分量的路径
    public static int s=0;
    public void qiu(int a[][],int l)//定义函数，参数a为二维数组，参数l为数组的维数
    {
        int t=0;//定义int型变量，进行数量的统计
        for(int i=1;i<l;i++)
        {
            for(int j=1;j<l;j++)//进行遍历，判断每一个节点是否有路通向其他节点
            {
                for(int m=1;m<l;m++)
                {
                    for(int n=1;n<l;n++)
                    {
                        if(a[m][n]==-1)
                        {
                            a[m][n]=1;//将走过的路归1
                        }
                    }
                }
                if(a[i][j]==1)//如果是1就有通向其他节点的路
                {
                    lu=lu+String.valueOf(i)+"--->"+String.valueOf(j)+"--->";//将这个节点加在路上
                    qiu1(a,l,i,j);//进行dfs遍历
                    lu="";
                }
                else//如果不是1就有通向其他节点的路,单独是一个强连通图
                {
                    t++;
                    if(t==l-1)
                    {
                        t=0;
                        System.out.println("强连通图为:"+i);
                    }
                }
            }
            t=0;
        }
    }
    public void qiu1(int a[][],int l,int i,int k)//dfs遍历算法中+是否有回路的算法，参数a为2维数组，l为数组的维数，i为dfs遍历时初始的节点，k为i指向的下一个节点
    {
        
        for(int m=1;m<l;m++)//从节点k进行遍历，看是否有指向其他节点的路
        {
            if(a[k][m]==1)//如果是1就存在路
            {
                a[k][m]=-1;//将走过的路封死，不能再走
                if(m==i)//判断是否为初始节点，如果是，就说明有回路，也就是强连通分量存在
                {
                    System.out.println("强连通路径为:"+lu+String.valueOf(m));//输出这个强连通分量图
                }
                else//如果不等于初始节点，说明有指向其他节点的路，继续进行dfs遍历
                {
        
                    lu=lu+String.valueOf(m)+"--->";
                    
                    qiu1(a,l,i,m);//递归判断下一个节点
                }
            }
        }
        int lengh=lu.length();//如果没路则说明走不通，就往回走，
        if(lengh>0)
        {
        lu=lu.substring(0, lengh-5);//将走过的路回收
        }
    }
}
public class Qiang {

    public static void main(String[] args) {
        // TODO 自动生成的方法存根
        int l,i,j,s;
        Qiufenliang zhao=new Qiufenliang();//定义求强连通分量的对象
        Scanner in=new Scanner(System.in);
        System.out.print("请输入顶点的个数:");
        l=in.nextInt();
        System.out.print("请输入边的个数:");
        s=in.nextInt();
        int a[][]=new int[l+1][l+1];
        for(int m=1;m<l+1;m++)
        {
            for(int n=1;n<l+1;n++)
            {
                a[m][n]=0;
            }
        }//将2维数组全部初始化为0
        for(int k=0;k<s;k++)
        {
            System.out.print("请输入第"+(k+1)+"条边的起点和终点"+"(起点和终点必须小于等于"+l+"):");
            i=in.nextInt();
            j=in.nextInt();
            a[i][j]=1;
        }//如果有一个节点指向下一节点，则将之变为1
        for(int m=1;m<l+1;m++)
        {
            for(int n=1;n<l+1;n++)
            {
                System.out.print(a[m][n]+"\\t");
            }
            System.out.println();
        }//输出这个二维数组
        zhao.qiu(a,l+1);//求强连通分量
    
    }

}

下面是一个有向图：

可以看出强连通分量为:1---->2---->3---->5---->1     4---->5---->1---->4

下面是另外的一个有向图：

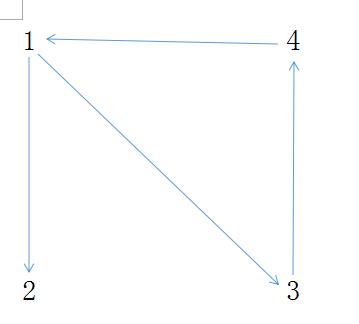
可以看出强连通分量为：1---->3---->4      还有一个单独的：2

如果有不理解的可以问我哦！