如何寻找已知轮廓的最大内接圆
Posted GreenOpen专注图像处理
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何寻找已知轮廓的最大内接圆相关的知识,希望对你有一定的参考价值。
问题的提出:
所谓内切圆,是指“与多边形各边都相切的圆“。我们这里需要找的是所谓”内接圆“,可以简单认为是”圆点在轮廓中,到轮廓中所有点的距离一样的图像“。在这所有的”内接圆“中,寻找半径最大的哪一个。这个问题已经广泛讨论了,比如

这样的图像,寻找轮廓的最大内接圆。
解决方法:
利用计算机图像学技术中轮廓的相关思路,可以直接从圆的定义解决此问题。基于OpenCV的代码和注释如下:
#include "stdafx.h"
#include <iostream>
using namespace std;
using namespace cv;
VP FindBigestContour(Mat src){
int imax = 0; //代表最大轮廓的序号
int imaxcontour = -1; //代表最大轮廓的大小
std::vector<std::vector<cv::Point>>contours;
findContours(src,contours,CV_RETR_LIST,CV_CHAIN_APPROX_SIMPLE);
for (int i=0;i<contours.size();i++){
int itmp = contourArea(contours[i]);//这里采用的是轮廓大小
if (imaxcontour < itmp ){
imax = i;
imaxcontour = itmp;
}
}
return contours[imax];
}
int main(int argc, char* argv[])
{
Mat src = imread("e:/template/cloud.png");
Mat temp;
cvtColor(src,temp,COLOR_BGR2GRAY);
threshold(temp,temp,100,255,THRESH_OTSU);
imshow("src",temp);
//寻找最大轮廓
VP VPResult = FindBigestContour(temp);
//寻找最大内切圆
int dist = 0;
int maxdist = 0;
Point center;
for(int i=0;i<src.cols;i++)
{
for(int j=0;j<src.rows;j++)
{
dist = pointPolygonTest(VPResult,cv::Point(i,j),true);
if(dist>maxdist)
{
maxdist=dist;
center=cv::Point(i,j);
}
}
}
//绘制结果
circle(src,center,maxdist,Scalar(0,0,255));
imshow("dst",src);
waitKey();
}
其中
PointPolygonTest
测试点是否在多边形中
double cvPointPolygonTest( const CvArr* contour, CvPoint2D32f pt, int measure_dist );
contour 输入轮廓.
pt 针对轮廓需要测试的点。
measure_dist 如果非0,函数将估算点到轮廓最近边的距离。
函数cvPointPolygonTest 决定测试点是否在轮廓内,轮廓外,还是轮廓的边上(或者共边的交点上),它的返回值是正负零,相对应的,当measure_dist=0时,返回值是1, -1,0, 同样当 measure_dist≠0 ,它是返回一个从点到最近的边的带符号距离。结果:
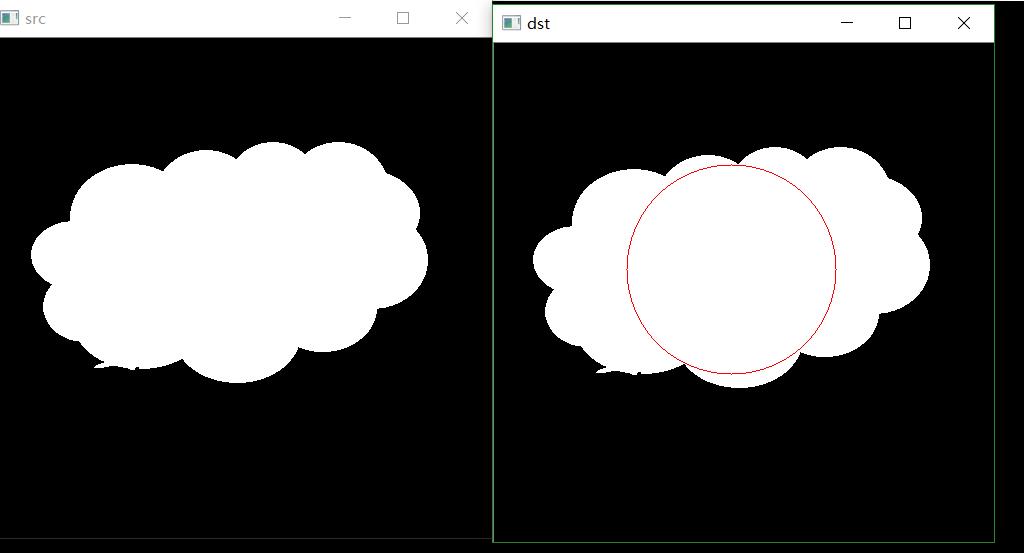
优化的思路:
这里对圆心的遍历,是遍历了所有的图像上面的点。然而根据”内接圆心一定在轮廓内部“这个先验知识,可以缩小循环范围,提高算法效率。
2018年7月27日22:01:01 对opencv的官方例子进行修改,并提交github
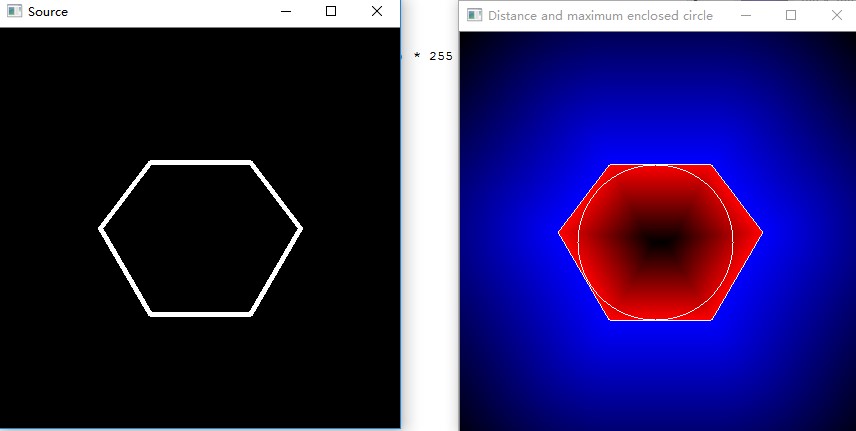
/**
* @function pointPolygonTest_demo.cpp
* @brief Demo code to use the pointPolygonTest function...fairly easy
* @author OpenCV team
*/
#include "stdafx.h"
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <iostream>
using namespace cv;
using namespace std;
//return the biggest contour by size
vector<Point> FindBiggestContour(Mat src){
int icount = 0;
int imaxcontour = -1;
std::vector<std::vector<cv::Point>>contours;
findContours(src,contours,CV_RETR_LIST,CV_CHAIN_APPROX_SIMPLE);
for (int i=0;i<contours.size();i++){
int itmp = contourArea(contours[i]);
if (imaxcontour < itmp ){
icount = i;
imaxcontour = itmp;
}
}
return contours[icount];
}
/**
* @function main
*/
int main( void )
{
/// Create an image
const int r = 100;
Mat src = Mat::zeros( Size( 4*r, 4*r ), CV_8U );
/// Create a sequence of points to make a contour
vector<Point2f> vert(6);
vert[0] = Point( 3*r/2, static_cast<int>(1.34*r) );
vert[1] = Point( 1*r, 2*r );
vert[2] = Point( 3*r/2, static_cast<int>(2.866*r) );
vert[3] = Point( 5*r/2, static_cast<int>(2.866*r) );
vert[4] = Point( 3*r, 2*r );
vert[5] = Point( 5*r/2, static_cast<int>(1.34*r) );
/// Draw it in src
for( int i = 0; i < 6; i++ )
{
line( src, vert[i], vert[(i+1)%6], Scalar( 255 ), 3 );
}
/// Get the contours
vector<vector<Point> > contours;
findContours( src, contours, RETR_TREE, CHAIN_APPROX_SIMPLE);
/// Calculate the distances to the contour
Mat raw_dist( src.size(), CV_32F );
for( int i = 0; i < src.rows; i++ )
{
for( int j = 0; j < src.cols; j++ )
{
raw_dist.at<float>(i,j) = (float)pointPolygonTest( contours[0], Point2f((float)j, (float)i), true );
}
}
double minVal, maxVal;
minMaxLoc( raw_dist, &minVal, &maxVal );
minVal = abs(minVal);
maxVal = abs(maxVal);
/// Depicting the distances graphically
Mat drawing = Mat::zeros( src.size(), CV_8UC3 );
for( int i = 0; i < src.rows; i++ )
{
for( int j = 0; j < src.cols; j++ )
{
if( raw_dist.at<float>(i,j) < 0 )
{
drawing.at<Vec3b>(i,j)[0] = (uchar)(255 - abs(raw_dist.at<float>(i,j)) * 255 / minVal);
}
else if( raw_dist.at<float>(i,j) > 0 )
{
drawing.at<Vec3b>(i,j)[2] = (uchar)(255 - raw_dist.at<float>(i,j) * 255 / maxVal);
}
else
{
drawing.at<Vec3b>(i,j)[0] = 255;
drawing.at<Vec3b>(i,j)[1] = 255;
drawing.at<Vec3b>(i,j)[2] = 255;
}
}
}
//get the biggest Contour
vector<Point> biggestContour = FindBiggestContour(src);
//find the maximum enclosed circle
int dist = 0;
int maxdist = 0;
Point center;
for(int i=0;i<src.cols;i++)
{
for(int j=0;j<src.rows;j++)
{
dist = pointPolygonTest(biggestContour,cv::Point(i,j),true);
if(dist>maxdist)
{
maxdist=dist;
center=cv::Point(i,j);
}
}
}
circle(drawing,center,maxdist,Scalar(255,255,255));
/// Show your results
imshow( "Source", src );
imshow( "Distance and maximum enclosed circle", drawing );
waitKey();
return 0;
}附件列表
以上是关于如何寻找已知轮廓的最大内接圆的主要内容,如果未能解决你的问题,请参考以下文章
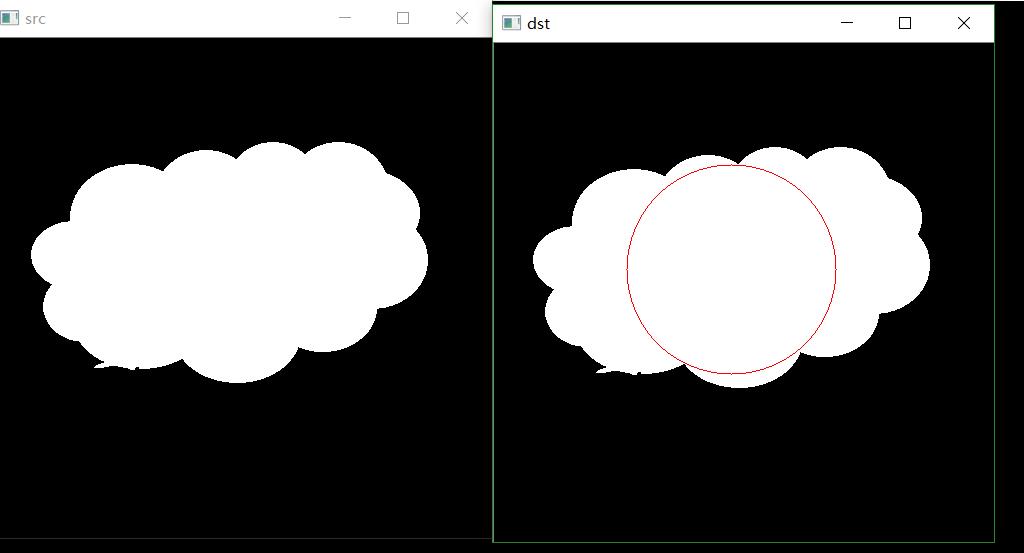 所谓内切圆,是指“与多边形各边都相切的圆“。我们这里需要找的是所谓”内接圆“,可以简单认为是”圆点在轮廓中,到轮廓中所有点的距离一样的图像“。在这所有的”内接圆“中,寻找半径最大的哪一个。
这个问题已经广泛讨论了。这里基于OpenCV进行代码实现,并提出优化思路。
所谓内切圆,是指“与多边形各边都相切的圆“。我们这里需要找的是所谓”内接圆“,可以简单认为是”圆点在轮廓中,到轮廓中所有点的距离一样的图像“。在这所有的”内接圆“中,寻找半径最大的哪一个。
这个问题已经广泛讨论了。这里基于OpenCV进行代码实现,并提出优化思路。