最小二乘与最大似然估计之间的关系
Posted neu博
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最小二乘与最大似然估计之间的关系相关的知识,希望对你有一定的参考价值。
1、结论
测量误差(测量)服从高斯分布的情况下, 最小二乘法等价于极大似然估计。
2、最大似然估计
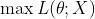
最大似然估计就是通过求解最大的(1)式得到参数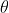 ,其中 L 函数称为参数
,其中 L 函数称为参数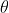 的似然函数,是一个概率分布函数。
的似然函数,是一个概率分布函数。
似然估计的思想是:测量值 X 是服从概率分布的,求概率模型中的参数,使得在假设的分布下获得该组测量出现概率最大:
例如:通过一次测量得到1.9、1.9、2.0、2.1、2.0、1.9、1.5、2.5、2.0、2.0,
通过直觉我们发现这组测量比较符合期望为2的高斯分布。
要不然,为什么取值都在2附近呢,为啥测量数据中没有(很少)1.0、5.0呢?也就是说,可以认为我的这些测量
是符合某个概率分布的(这个例子中为高斯分布),测量值中得到2附近值的概率比较大。
例如:一个箱子里有红球和黑球,通过10次放回抽取实验得到的结果为:8次黑球、2次红球。问箱子中黑球的比例?
这个例子中箱子里只有红球和黑球,可以假设黑球的比例为 p ,那么红球的概率为(1-p),
那么10次实验中8次黑球、两次红球的概率为: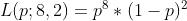
以上是关于最小二乘与最大似然估计之间的关系的主要内容,如果未能解决你的问题,请参考以下文章