哈弗曼树及其操作
Posted Mr.Zhao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了哈弗曼树及其操作相关的知识,希望对你有一定的参考价值。
1.哈弗曼树的节点声明
1 package com.neusoft.Tree; 2 3 public class HuffmanNode { 4 public int weight; 5 //加入哈夫曼树的标志,flag=0表示该节点没有加入哈夫曼树,=1表示加入 6 public int flag; 7 public HuffmanNode parent,lchild,rchild; 8 public HuffmanNode() { 9 this(0); 10 } 11 public HuffmanNode(int weight){ 12 this.weight=weight; 13 flag=0; 14 parent=lchild=rchild=null; 15 } 16 }
点击可复制代码

1 package com.neusoft.Tree; 2 3 public class HuffmanNode { 4 public int weight; 5 //加入哈夫曼树的标志,flag=0表示该节点没有加入哈夫曼树,=1表示加入 6 public int flag; 7 public HuffmanNode parent,lchild,rchild; 8 public HuffmanNode() { 9 this(0); 10 } 11 public HuffmanNode(int weight){ 12 this.weight=weight; 13 flag=0; 14 parent=lchild=rchild=null; 15 } 16 }
2.哈夫曼编码的构建及测试
1 package com.neusoft.Tree; 2 /** 3 * @author zhao-chj 4 * 哈夫曼树及其操作 5 */ 6 public class HuffmanTree { 7 8 //求哈夫曼编码的算法,w存放n个字符的权值 9 public int[][] huffmanCoding (int[] w){ 10 int n= w.length;//哈夫曼树的字符个数 11 int m=2*n-1;//哈夫曼树的节点个数 12 HuffmanNode[] HN =new HuffmanNode[m]; 13 int i=0; 14 for (i = 0; i< n; i++) { 15 HN[i] = new HuffmanNode(w[i]);//构造n个具有权值的节点 16 } 17 for (i = n; i< m; i++) { 18 HuffmanNode min1=selectMin(HN,i-1); 19 min1.flag=1;//表示已标记 20 HuffmanNode min2=selectMin(HN, i-1); 21 min2.flag=1; 22 //构造min1和min2的父节点,并且修改权值 23 HN[i] =new HuffmanNode(); 24 min1.parent=HN[i]; 25 min2.parent=HN[i]; 26 HN[i].lchild=min1; 27 HN[i].rchild=min2; 28 HN[i].weight=min1.weight+min2.weight; 29 } 30 //从叶子节点到根逆向求每个字符的哈夫曼编码 31 int[][] HuffCode =new int[n][n];//分配n个字符编码存储空间 32 for (int j = 0; j <n; j++) { 33 int start=n-1;//编码的开始位置,初始化为数组的结尾 34 for (HuffmanNode c=HN[j],p=c.parent; p!=null; c=p,p=p.parent) { 35 //从叶子结点到根逆向求解编码 36 if (p.lchild.equals(c)) {//左孩子编码为0 37 HuffCode[j][start--] =0; 38 }else { 39 //右孩子编码为1 40 HuffCode[j][start--]=1; 41 } 42 HuffCode[j][start]=-1;//编码的开始标志为-1 43 } 44 } 45 return HuffCode; 46 } 47 /** 48 * 在HN[0...i-1]选择不再哈夫曼树中且weight最小的节点 49 */ 50 private HuffmanNode selectMin(HuffmanNode[] HN, int end) { 51 HuffmanNode min=HN[end]; 52 for (int i = 0; i < end; i++) { 53 HuffmanNode h=HN[i]; 54 if (h.flag==0&&h.weight<min.weight) { 55 //不再哈夫曼树中且weight最小的节点 56 min=h; 57 } 58 } 59 return min; 60 } 61 public static void main(String[] args) { 62 int [] w={23,11,5,3,29,14,7,8}; 63 HuffmanTree T =new HuffmanTree();//构造哈夫曼树 64 int [][] HN=T.huffmanCoding(w);//求哈夫曼编码 65 System.out.println("哈夫曼编码为:"); 66 for (int i = 0; i < HN.length; i++) { 67 System.out.print(w[i]+" "); 68 for (int j = 0; j < HN[i].length; j++) { 69 if (HN[i][j] ==-1 ) {//数组结尾标志 70 for (int k = j+1; k < HN[i].length; k++) { 71 System.out.print(HN[i][k]); 72 } 73 break; 74 } 75 } 76 System.out.println(); 77 } 78 } 79 }
点击可复制代码

1 package com.neusoft.Tree; 2 /** 3 * @author zhao-chj 4 * 哈夫曼树及其操作 5 */ 6 public class HuffmanTree { 7 8 //求哈夫曼编码的算法,w存放n个字符的权值 9 public int[][] huffmanCoding (int[] w){ 10 int n= w.length;//哈夫曼树的字符个数 11 int m=2*n-1;//哈夫曼树的节点个数 12 HuffmanNode[] HN =new HuffmanNode[m]; 13 int i=0; 14 for (i = 0; i< n; i++) { 15 HN[i] = new HuffmanNode(w[i]);//构造n个具有权值的节点 16 } 17 for (i = n; i< m; i++) { 18 HuffmanNode min1=selectMin(HN,i-1); 19 min1.flag=1;//表示已标记 20 HuffmanNode min2=selectMin(HN, i-1); 21 min2.flag=1; 22 //构造min1和min2的父节点,并且修改权值 23 HN[i] =new HuffmanNode(); 24 min1.parent=HN[i]; 25 min2.parent=HN[i]; 26 HN[i].lchild=min1; 27 HN[i].rchild=min2; 28 HN[i].weight=min1.weight+min2.weight; 29 } 30 //从叶子节点到根逆向求每个字符的哈夫曼编码 31 int[][] HuffCode =new int[n][n];//分配n个字符编码存储空间 32 for (int j = 0; j <n; j++) { 33 int start=n-1;//编码的开始位置,初始化为数组的结尾 34 for (HuffmanNode c=HN[j],p=c.parent; p!=null; c=p,p=p.parent) { 35 //从叶子结点到根逆向求解编码 36 if (p.lchild.equals(c)) {//左孩子编码为0 37 HuffCode[j][start--] =0; 38 }else { 39 //右孩子编码为1 40 HuffCode[j][start--]=1; 41 } 42 HuffCode[j][start]=-1;//编码的开始标志为-1 43 } 44 } 45 return HuffCode; 46 } 47 /** 48 * 在HN[0...i-1]选择不再哈夫曼树中且weight最小的节点 49 */ 50 private HuffmanNode selectMin(HuffmanNode[] HN, int end) { 51 HuffmanNode min=HN[end]; 52 for (int i = 0; i < end; i++) { 53 HuffmanNode h=HN[i]; 54 if (h.flag==0&&h.weight<min.weight) { 55 //不再哈夫曼树中且weight最小的节点 56 min=h; 57 } 58 } 59 return min; 60 } 61 public static void main(String[] args) { 62 int [] w={23,11,5,3,29,14,7,8}; 63 HuffmanTree T =new HuffmanTree();//构造哈夫曼树 64 int [][] HN=T.huffmanCoding(w);//求哈夫曼编码 65 System.out.println("哈夫曼编码为:"); 66 for (int i = 0; i < HN.length; i++) { 67 System.out.print(w[i]+" "); 68 for (int j = 0; j < HN[i].length; j++) { 69 if (HN[i][j] ==-1 ) {//数组结尾标志 70 for (int k = j+1; k < HN[i].length; k++) { 71 System.out.print(HN[i][k]); 72 } 73 break; 74 } 75 } 76 System.out.println(); 77 } 78 } 79 }
3.测试及运行结果
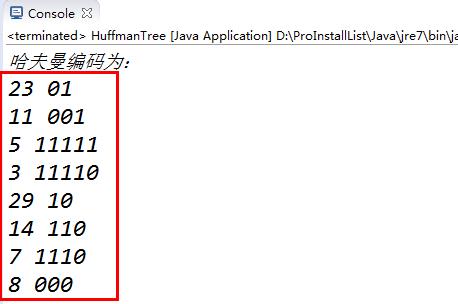
以上是关于哈弗曼树及其操作的主要内容,如果未能解决你的问题,请参考以下文章
