机器学习笔记（Washington University）- Regression Specialization-week four

Posted 2020-09-16

1. Ridge regression

A way to automatically balance between bias and varaince situations and regulate

overfitting when using many features. because the model has a lot of flexibility to explain

the data.

 

2. Overfitting

Formally, when we can find a model with higher traning error but lower true error compared

with the trained model, then the trained model is overfiting the dataset.

Overfitting is associated with very large magnitude estimated coefficients.

And Not like enough data,if we have few observations, the model will overfit rapidly as the

model complexity increases.

 

3. Desired total cost

want to balance:

1. How well function fits data.

2. Magnitude of coefficientrs.

Total cost = measure of fit + measure of magnitude of coefficients

measure of magnitude of coefficients = sum of squares  of regression coefficients (L2 Norm)

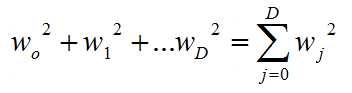
so the regression is selected to minimize:

 

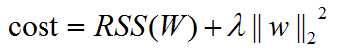(lambda is the tuning parameter)

when lambda is small, just as before,  W = W(least square solution)

when lambda is large, W = 0

when lambda is in between, then  0<= |W|<=W(least square solution)

so the lambda is controlling the model complexity.

 

4. The formula for the new gradient

 

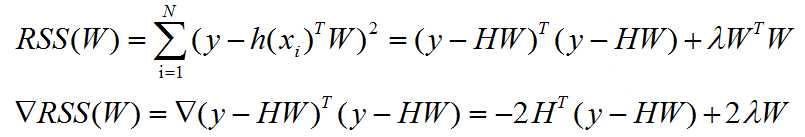
5. solution

Close-form :

we can set the gradient to zero, and we can get the solution like shown below

 

 

 

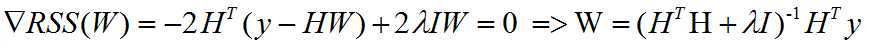
when lambda is zero, it is the old solution,

when lambda is infinity, we are like to divide by infinity, so the solution to W is zero

the first item is invertible, even if the observations (N) is smaller than D(faetures)

when the intercept is kept out from shrinking, we just set the (1,1)  element of I to be zero

 

Gradient descent:

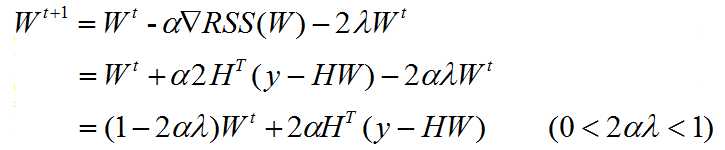
The interpretation of this formula is:

No matter what, we firstly shrink the W vector, then we modify it to fit our data.

when the intercept is kept out from shrinking, we just add a if-statement to set 

the w0 to update just like the old solution. no lambda involved.

 

6. K-fold cross validataion

The data set is divided into K blocks

For a certain lambda

For K=1...K

1. Estimate w on the training blocks

2.compute error on validation blocks: error_K(labda)

then we compute the average error of all the error_K, we will choose the best lamda to minimize this error.

leave-one-out cross validation just means that K=N(data size)

Typically, K=5 or 10