UVa 11149 矩阵的幂（矩阵倍增法模板题）

Posted 2020-09-16 谦谦君子，陌上其华

https://vjudge.net/problem/UVA-11149

题意：

输入一个n×n矩阵A，计算A+A^2+A^3+...A^k的值。

 

思路：

矩阵倍增法。

处理方法如下，一直化简下去直到变成A。

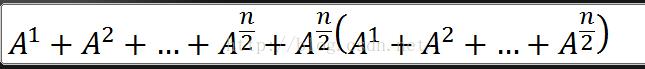
代码如下：

1 Matrix solve(Matrix base,int x)
2 {
3     if(x==1)return base;
4     Matrix temp=solve(base,x/2);
5     Matrix sum=add(temp,multi(pow(base,x/2),temp));
6     if(x&1)
7         sum=add(pow(base,x),sum);
8     return sum;
9 }

 

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<vector>
 6 #include<stack>
 7 #include<queue>
 8 #include<cmath>
 9 #include<map>
10 using namespace std;
11 
12 const int maxn=40+5;
13 const int MOD=10;
14 
15 int n,k;
16 
17 struct Matrix
18 {
19     int mat[maxn][maxn];
20 }base;
21 
22 Matrix multi(Matrix a,Matrix b)
23 {
24     Matrix temp;
25     for(int i=0;i<n;i++)
26     for(int j=0;j<n;j++)
27     {
28         temp.mat[i][j]=0;
29         for(int k=0;k<n;k++)
30             temp.mat[i][j]=(temp.mat[i][j]+a.mat[i][k]*b.mat[k][j])%MOD;
31     }
32     return temp;
33 }
34 
35 Matrix pow(Matrix a,int x)
36 {
37     Matrix res;
38     memset(res.mat,0,sizeof(res.mat));
39     for(int i=0;i<n;i++)  res.mat[i][i]=1;
40     while(x)
41     {
42         if(x&1)  res=multi(res,a);
43         a=multi(a,a);
44         x>>=1;
45     }
46     return res;
47 }
48 
49 Matrix add(Matrix a,Matrix b)
50 {
51     Matrix temp;
52     for(int i=0;i<n;i++)
53         for(int j=0;j<n;j++)
54         temp.mat[i][j]=(a.mat[i][j]+b.mat[i][j])%MOD;
55     return temp;
56 }
57 
58 Matrix solve(Matrix base,int x)
59 {
60     if(x==1)return base;
61     Matrix temp=solve(base,x/2);
62     Matrix sum=add(temp,multi(pow(base,x/2),temp));
63     if(x&1)
64         sum=add(pow(base,x),sum);
65     return sum;
66 }
67 
68 int main()
69 {
70     //freopen("D:\\\\input.txt","r",stdin);
71     while(~scanf("%d%d",&n,&k) &&n)
72     {
73         for(int i=0;i<n;i++)
74         for(int j=0;j<n;j++)
75         {
76             scanf("%d",&base.mat[i][j]);
77             base.mat[i][j]%=MOD;
78         }
79         Matrix ans=solve(base,k);
80         for(int i=0;i<n;i++)
81         {
82             for(int j=0;j<n;j++)
83             {
84                 if(j)  printf(" ");
85                 printf("%d",ans.mat[i][j]);
86             }
87             printf("\\n");
88         }
89         printf("\\n");
90     }
91     return 0;
92 }