决策树

Posted 2020-06-19 Speak Softly Love

http://www.cnblogs.com/fengfenggirl/p/classsify_decision_tree.html

决策树是一种基本的分类和回归方法。优点是具有可读性，分类速度快，学习时，利用训练数据，根据损失函数最小化得原则建立决策树模型。

缺点是容易过拟合，对训练数据的分类能力好，泛化能力差。

决策树通常分为3个部分：特征选择，决策树的生成和决策树的修剪。

决策树的学习算法通常是地跪地选择一个最优的特征，并根据该特征对训练数据进行分割，使得各个子数据集具有较好的分类过程，这个过程对应

着特征空间的划分，也对应这决策树的构建，开始，构建根结点，所有数据都放在根结点。

选择一个最优特征，按照这一特征将数据集划分为多个子集，这些子集有一个在当前条件下最好的分类。

如果这些子集已经能够被正确的分类，就构造叶子结点，并将这些子集放到对应的叶子结点中；

如果还有子集不能够被正确分类，就对这些子集选择最优特征，并继续进行分割。

如此递归进行下去，直到所有训练子集都能够被正确分类，或者没有合适的特征。

最后每个子集都被正确的分到叶子节点上，即有了明确的类。

决策树主要有ID3,C4.5,和CART算法。

ID3和C4.5的区别是特征划分的标准，一个是信息增益，一个是用信息增益比。

信息增益可以表示：

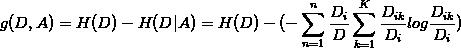
\\(g(D,A)=H(D)-H(D|A)\\) ,其中H()表示熵，熵越大代表不确定性越大。

这个公式的意义就在于，使用特征A进行分类后，整体的不确定性会大大减小。

但是这个公式是有个问题，它计算的是绝对值，如果在某些极端情况下，特征A有可以将每个样本变为树的节点，那H(D|A)就为0，

这时候信息增益最大，但这个并不是并不是我们想要的特征。同时如果一个特征值的经验熵大的时候，信息增益会偏大，这个时候，

使用信息增益比，会对该这种情况进行校正，这就是C4.5算法。

看到书上信息增益比的公式是：

我觉得这里的H(D)应该是H(A)。

 

分类与回归树（CART）算法假设决策树是一个二叉树，内部节点特征的取值为“是”和“否”，左边选取是的分支，右边选取否的分支。

这样的决策树等价于递归地二分每个特征，并将输入空间特征有效地划分为有限个单元，并在这些单元上确定的预测概率分布。

CART使用基尼指数进行计算

ID3算法实现：

# -*- coding: utf-8 -*-
import math
import operator
import numpy as np

class Id3(object):
    """
    决策树ID3算法实现
    """

    def __init__(self):
        pass

    def cal_entropy(self, data_set):
        """
        计算熵
        :param data_set: [1, 1, 1, 0, 0]
        :return:
        """
        num_entries = len(data_set)
        featrue_dict = {}
        for feature in data_set:
            lable = feature[-1]
            if lable in featrue_dict.keys():
                featrue_dict[lable] += 1
            else:
                featrue_dict[lable] = 1
        entropy = 0.0

        for key in featrue_dict.keys():
            prob = float(featrue_dict[key]) / num_entries
            if prob != 0:
                entropy -= prob * math.log(prob, 2)

        return entropy

    def get_sub_data(self, data_set, feat_index, value):
        """
        获取用来计算条件熵的部分数据
        :param data_set:
        :return:
        """
        sub_data = []
        num_entries = len(data_set)
        for i in xrange(num_entries):
            if data_set[i][feat_index] == value:
                sub_data.append([data_set[i][feat_index], data_set[i][-1]])

        return sub_data

    def get_max_info_gain_ratio_and_fature(self, data_set):
        """
        得到最大增益信息和对应的 feature
        :param data_set:
        :return: max_info_gain , feature
        """
        #初始化数据
        num_features = len(data_set[0]) - 1
        base_entropy = self.cal_entropy(data_set)
        max_info = 0.0
        max_feature = -1
        #计算每个特征的熵
        for i in xrange(num_features):
            feature = [sample[i] for sample in data_set]
            unique_feature_values = set(feature)
            tmp_entropy = 0.0
            for value in unique_feature_values:
                sub_data = self.get_sub_data(data_set, i, value)
                prob = len(sub_data) / float(len(data_set))
                tmp_entropy += prob * self.cal_entropy(sub_data)
            #保留最大增益信息和特征
            info_gain = base_entropy - tmp_entropy
            #info_gain_ratio = (base_entropy - tmp_entropy) / base_entropy
            if info_gain > max_info:
                max_info = info_gain
                max_feature = i
        return max_info, max_feature

    def get_majority_cnt(self, classlist):
        """
        获取数据集中实例数最大的类的名称
        :param classlist:
        :return:
        """
        class_count = {}
        for data in classlist:
            if data in class_count.keys():
                class_count[data] += 1
            else:
                class_count[data] = 0

        reverse_class_count = sorted(class_count.iteritems(), key=operator.itemgetter(1), reverse=True)

        return reverse_class_count[0][0]

    def split_data_set(self, data_set, feature_index, value):
        """
        去掉特征集合中对应的feather
        :param feature_index:
        :param value:
        :return:
        """
        res_data = []

        for sample in data_set:
            if sample[feature_index] == value:
                split_sample = sample[:feature_index]
                split_sample.extend(sample[feature_index+1:])
                res_data.append(split_sample)
        return res_data

    def creata_decision_tree(self, data_set , labels , threshold):
        """

        :param data_set: 数据集
        :param labels: 标签集
        :param threshold: 阈值
        :return: 返回一棵树
        """
        class_list = [example[-1] for example in data_set]

        #如果只有一种结果了,那就停止
        if class_list.count(class_list[0]) == len(class_list):
            return class_list[0]

        if len(data_set[0]) == 1:
            return self.get_majority_cnt(class_list)

        max_ratio, best_feature_index = self.get_max_info_gain_ratio_and_fature(data_set)
        feature_list = [example[best_feature_index] for example in data_set]

        if  max_ratio < threshold:
            return self.get_majority_cnt(feature_list)

        best_feature_label = labels[best_feature_index]
        my_tree = {best_feature_label: {}}
        del(labels[best_feature_index])

        unique_values = set(feature_list)
        for value in unique_values:
            sub_labels = labels[:]
            my_tree[best_feature_label][value] = self.creata_decision_tree(self.split_data_set(data_set,
                                                                                               best_feature_index,
                                                                                               value),
                                                                           sub_labels, threshold)
        return my_tree

    def classify(self, inputTree, featLabels, testVec):
        firstStr = inputTree.keys()[0]
        secondDict = inputTree[firstStr]
        featIndex = featLabels.index(firstStr)
        for key in secondDict.keys():
            if testVec[featIndex] == key:
                if type(secondDict[key]).__name__ == \'dict\':
                    classLabel = self.classify(secondDict[key], featLabels, testVec)
                else: classLabel = secondDict[key]
        return classLabel

if __name__ == \'__main__\':
    obj = Id3()
    data_set = [[1,1,\'yes\'],
               [1,1, \'yes\'],
               [1,0,\'no\'],
               [0,1,\'no\'],
               [0,1,\'no\']]
    labels = [\'no surfacing\',\'flippers\']
    create_labels = labels[:]
    tree = obj.creata_decision_tree(data_set, create_labels, 0.1)
    print obj.classify(tree, labels, [1, 0])

View Code

CART算法实现：

# -*- coding: utf-8 -*-
"""
classfication and regression tree
分类与回归树
"""
import operator

class Node(object):
    def __init__(self, feat, val, left=None, right=None, result=None):
        self.feature = feat
        self.split_value = val
        self.left_node = left
        self.right_node = right
        self.result = result

class Cart(object):
    """
    分类与回归树, 假设决策树为二叉树
    """
    def __init__(self):
        pass

    def cal_gini(self, data_set, num_samples):
        """
        计算基尼指数, 1 - sum(pi)
        :param data_set:
        :return:
        """
        num_entries = num_samples
        featrue_dict = {}
        for feature in data_set:
            lable = feature[-1]
            if lable in featrue_dict.keys():
                featrue_dict[lable] += 1
            else:
                featrue_dict[lable] = 1

        temp = 0.0
        for key in featrue_dict.keys():
            prob = float(featrue_dict[key]) / num_entries
            temp += pow(prob, 2)

        return 1 - temp

    def get_sub_data(self, data_set, feat_index, value):
        """
        获取用来计算条件熵的部分数据
        :param data_set:
        :return:
        """
        sub_data = []
        num_entries = len(data_set)
        for i in xrange(num_entries):
            if data_set[i][feat_index] == value:
                sub_data.append([data_set[i][feat_index], data_set[i][-1]])

        return sub_data

    def get_best_feature_and_split(self, data_set):
        """
        遍历每一个特征A,对其可能取值a,计算A=a的时候的基尼指数
        :param data_set:
        :return:
        """
        #样本个数
        num_samples = len(data_set)
        #特征个数
        num_features = len(data_set[0]) - 1
        #最小GINI和最佳feature
        min_gini = 9999.0
        best_feature_index = -1
        split_val = None
        for i in xrange(0, num_features):
            #计算特征值的每个变量的GINI
            feature = [example[i] for example in data_set]
            unique_feature = set(feature)
            for val in unique_feature:
                data_include_val, data_exclude_val = self.split_data(data_set, i, val)
                gini_data_include_val = self.cal_gini(data_include_val, num_samples)
                gini_data_include_val *= float(len(data_include_val)) / num_samples
                gini_data_exclude_val = self.cal_gini(data_exclude_val, num_samples)
                gini_data_exclude_val *= float(len(data_exclude_val)) / num_samples
                gini = gini_data_include_val + gini_data_exclude_val
                if gini < min_gini:
                    min_gini = gini
                    best_feature_index = i
                    split_val = val

        return best_feature_index, split_val

    def split_data(self, data_set, feature_index, split_value):
        """
        分割数据,对于每个特征的取值a,分为两类,一类特征取值为a,一类特征取值不为a
        :param data_set:
        :param feature_index: 特征值下标
        :param split_value: 分割的值
        :return:
        """
        #特征值为a的list
        data_include_a = []
        #特征值不为a的list
        data_exclude_a = []
        for example in data_set:
            tmp_list = example[:feature_index]
            tmp_list.extend(example[feature_index + 1:])

            if example[feature_index] == split_value:
                data_include_a.append(tmp_list)
            else:
                data_exclude_a.append(tmp_list)

        return data_include_a, data_exclude_a

    def get_majority_cnt(self, classlist):
        """
        获取数据集中实例数最大的类的名称
        :param classlist:
        :return:
        """
        class_count = {}
        for data in classlist:
            if data in class_count.keys():
                class_count[data] += 1
            else:
                class_count[data] = 0

        reverse_class_count = sorted(class_count.iteritems(), key=operator.itemgetter(1), reverse=True)

        return reverse_class_count[0][0]

    def build_cart_tree(self, data_set):
        """
        创建树
        :param data_set:
        :return:
        """

        class_list = [example[-1] for example in data_set]

        #如果只有一种结果了,那就停止
        if class_list.count(class_list[0]) == len(class_list):
            return Node(None, None, result=class_list[0])

        feature_index, split_val = self.get_best_feature_and_split(data_set)
        m1, m2 = self.split_data(data_set, feature_index, split_val)
        root = Node(feature_index, split_val)
        root.left_node = self.build_cart_tree(m1)
        root.right_node = self.build_cart_tree(m2)

        return root

    def cart_classfy(self, root, test_vec):
        if root.feature is None:
            return root.result

        if test_vec[root.feature] == root.split_value:
            return self.cart_classfy(root.left_node, test_vec)
        else:
            return self.cart_classfy(root.right_node, test_vec)

if __name__ == \'__main__\':
    obj = Cart()
    data_set = [[1,1,\'yes\'],
               [1,1, \'yes\'],
               [1,0,\'no\'],
               [0,1,\'no\'],
               [0,1,\'no\']]
    labels = [\'no surfacing\',\'flippers\']
    create_labels = labels[:]
    tree = obj.build_cart_tree(data_set)
    print obj.cart_classfy(tree, [1, 0])

View Code