51nod 1228 序列求和

Posted 2020-09-15 ws_ccd

伯努利数，刚！

自然数幂和神犇的blog：  http://blog.csdn.net/acdreamers/article/details/38929067

伯努利数的2个重要的式子：

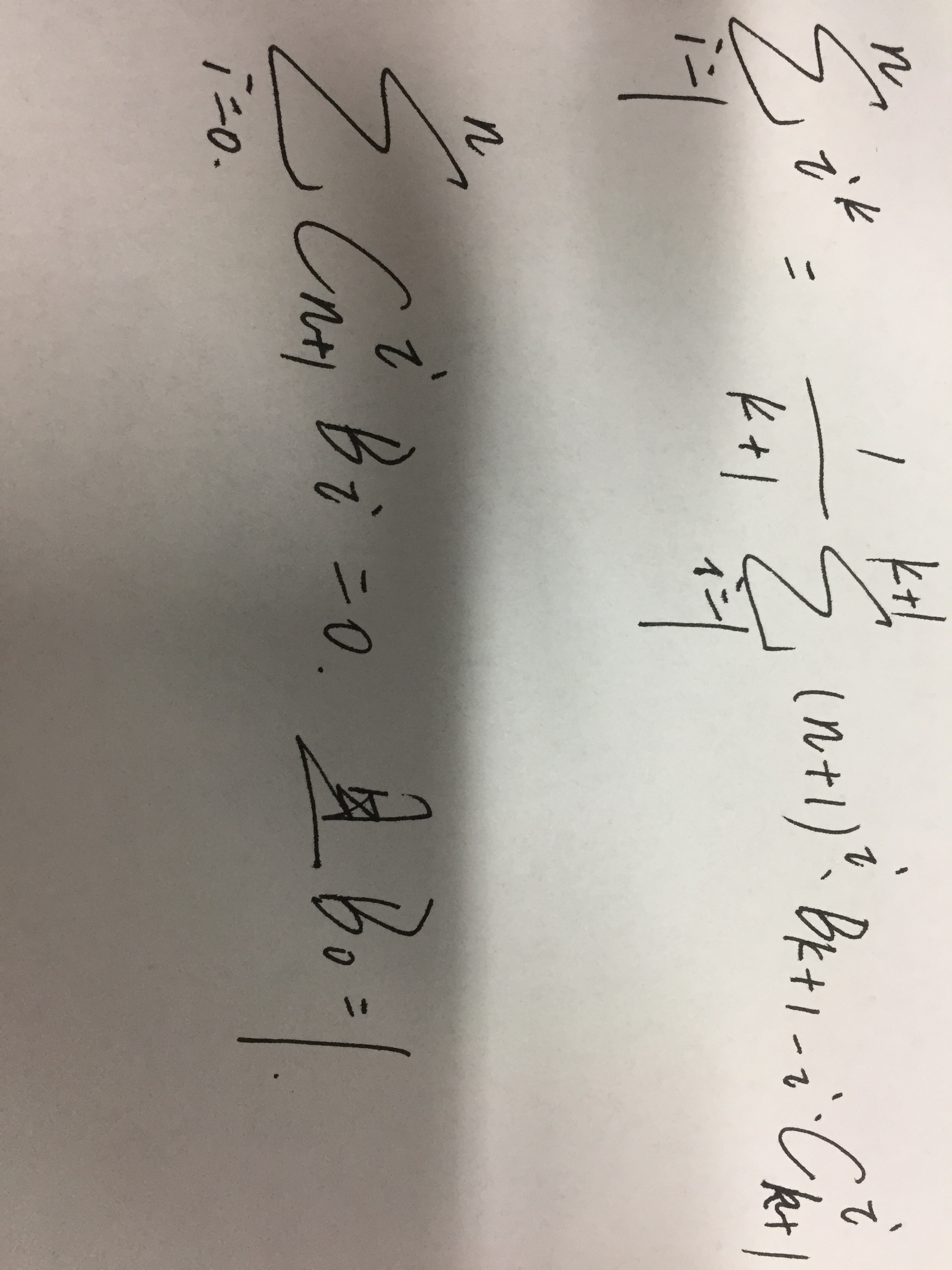
为什么图片这么大。。。

这样的话n^2预处理出伯努利数，然后就可做了

 1 #include <bits/stdc++.h>
 2 #define LL long long
 3 using namespace std;
 4 
 5 const int M=2005;
 6 const int maxn=2050;
 7 const int mod=1000000007;
 8 
 9 
10 int fac[maxn],inv[maxn],facinv[maxn];
11 void pre_C()
12 {
13     fac[0]=inv[1]=inv[0]=facinv[1]=facinv[0]=1;
14     for (int i=1; i<=M; i++) fac[i]=(LL)fac[i-1]*i%mod;
15     for (int i=2; i<=M; i++) inv[i]=(LL)(mod-mod/i)*inv[mod%i]%mod;
16     for (int i=2; i<=M; i++) facinv[i]=(LL)inv[i]*facinv[i-1]%mod;
17 }
18 LL C(int n, int m)
19 {
20     return (LL) fac[n]*facinv[m]%mod*facinv[n-m]%mod;
21 }
22 
23 int B[maxn];
24 void pre_B()
25 {
26     B[0]=1;
27     for (int i=1; i<=M; i++)
28     {
29         int ans=0;
30         for (int j=0; j<i; j++) ans=(ans+(LL)C(i+1,j)*B[j]%mod)%mod;
31         ans=(LL)ans*(-inv[i+1])%mod;
32         ans=(ans+mod)%mod;
33         B[i]=ans;
34     }
35 }
36 
37 int tmp[maxn];
38 int work(int k)
39 {
40     LL ans=inv[k+1],sum=0;
41     for (int i=1; i<=k+1; i++)
42         sum=(sum+C(k+1,i)*tmp[i]%mod*B[k+1-i]%mod)%mod;
43     ans=ans*sum%mod;
44     return ans%mod;
45 }
46 
47 LL n; 
48 int k;
49 int main()
50 {
51     pre_C(); pre_B();
52     int T; scanf("%d",&T);
53     while (T--)
54     {
55         scanf("%I64d %d",&n,&k);
56         n%=mod; tmp[0]=1;
57         for (int i=1; i<=M; i++) tmp[i]=(LL)tmp[i-1]*(n+1)%mod;
58         printf("%d\\n",work(k));
59     }
60     return 0;
61 }