算法学习——莫比乌斯反演
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法学习——莫比乌斯反演相关的知识,希望对你有一定的参考价值。
。。
省选GG了,我果然还是太菜了。。
突然想讲莫比乌斯反演了
那就讲吧!
首先我们看一个等式——
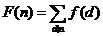
(d|n表示d是n的约束)
然后呢,转换一下
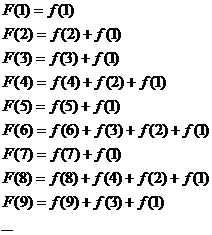
于是,我们就发现!
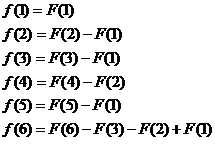
没错!F的系数是有规律的!
规律is here!
公式:
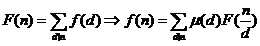
这个有什么卵用呢?
假如说有一道题
F(n)可以很simple的求出来而求f(n)就比较difficult了,该怎么办呢?
然后就可以用上面的式子了
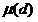 是莫比乌斯函数,十分有趣
是莫比乌斯函数,十分有趣
定义如下:
若d=1,则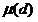 =1
=1
若d=p1*p2*p3...*pk,且pi为互异素数,则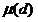 =(-1)^k
=(-1)^k
否则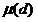 =0
=0
然后,莫比乌斯函数有一些奇(luan)奇(qi)怪(ba)怪(zao)的性质——
1、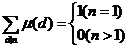
这个嘛。。二项式定理算一下就推出来了
2、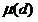 是积性函数。什么是积性函数?即对于所有互质的x,y,f(x)*f(y)=f(x*y),嗯,积性函数的前缀和也是积性函数。
是积性函数。什么是积性函数?即对于所有互质的x,y,f(x)*f(y)=f(x*y),嗯,积性函数的前缀和也是积性函数。
于是,你就能看到莫比乌斯反演的神奇之处了!
来看一道题
Bzoj2301 Problem b
题意
给你T组a,b,c,d,k求(a<=x<=b,c<=y<=d)有多少组gcd(x,y)=k
T<=50000,a<=b<=50000,c<=d<=50000
设p[x][y]为(1<=a<=x,1<=b<=y)中,gcd(a,b)=1的个数
所以,ans=p[b/k][d/k]-p[b/k][c/k]-p[a/k][d/k]+p[a/k][b/k](容斥233,可以抽象成一个平面)
然后,设f(i)为(1<=x<=n,1<=y<=m)gcd(x,y)==i的个数
发现——很难求。。但我们可以设F(i)为(1<=x<=n,1<=y<=m)i|gcd(x,y)的个数
这个求起来就非常simple了!
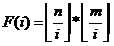 很显然。。
很显然。。
然后,根据莫比乌斯反演的公式——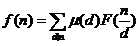
就可以做了!
哦对了,莫比乌斯函数是可以线性筛出来的,那个叫杜教筛,可以baidu一下
推一下式子——
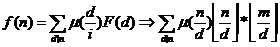
然后。。暴力枚举k的倍数。。就可以做了。
But!O(n)是GG的!所以我们要加优化!
仔细一看,发现 有
有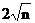 个取值,所以
个取值,所以
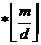 有
有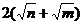 个取值,只要暴力枚举这些取值,维护一下前缀和就好了
个取值,只要暴力枚举这些取值,维护一下前缀和就好了
最后,顺便%一下PoPoQQQ:https://wenku.baidu.com/view/fbec9c63ba1aa8114431d9ac.html
End.
以上是关于算法学习——莫比乌斯反演的主要内容,如果未能解决你的问题,请参考以下文章