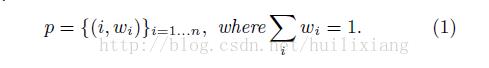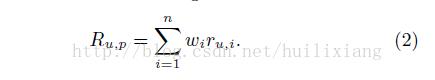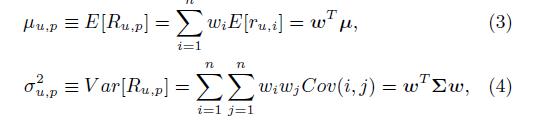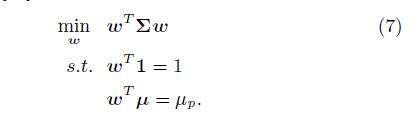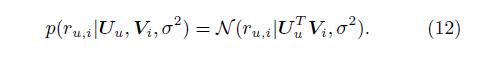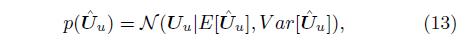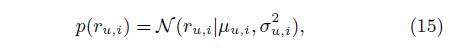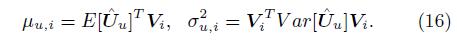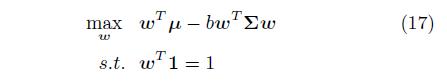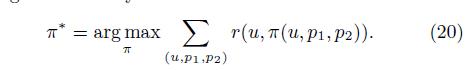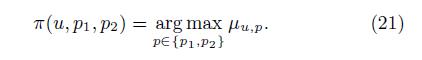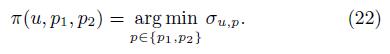从风险管理的角度来看是否须要个性化推荐
Posted liguangsunls
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从风险管理的角度来看是否须要个性化推荐相关的知识,希望对你有一定的参考价值。
一 背景
1、现今 ,个性化技术被广泛用于推荐系统 。 特别是基于用户的偏好数据进行个性化预測的
协同过滤算法,已被证是实际可行的。然而 在某种程度上我们并不知道个性化推荐是否总是
能优于非个性化推荐.《Performance of recommender algorithms on top-n recommendation
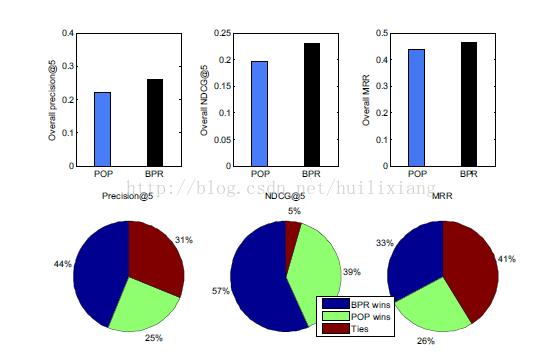
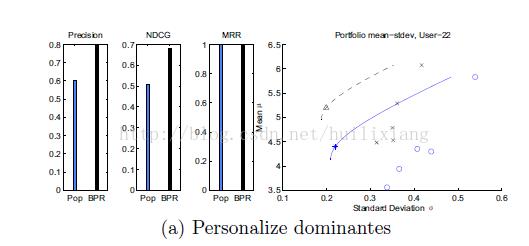
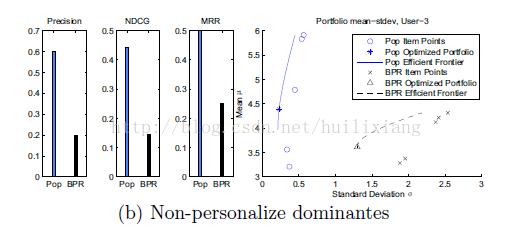
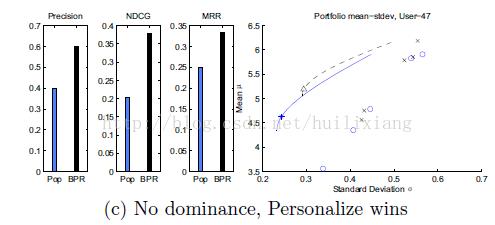
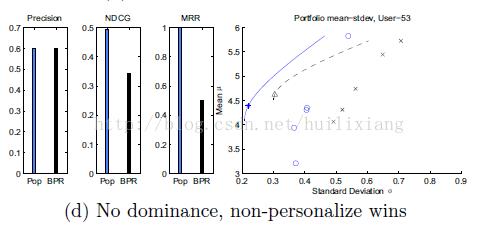
tasks》已证实基于热门的推荐也有相当好的效果。下图是Bayesian personalized ranking
和 popularity-based 推荐算法的结果比較(基于MovieLens的数据集)。
尽管总体上BPR算法占优 , 可是也有非常大的部分热门占优。三个图分别基于不同的推荐
结果精确度评定算法。
详细见Learning to Rank for IR的评价指标
2、从学习模式的角度来看 , 个性推荐能预測出用户的偏好。但会非常敏感 。非个性化推
荐相反。如何比較个性化推荐和非个性推荐?我们引入金融领域的风险管理的概念。我
们通过使用MPT(Modern Portfolio Theory)来对推荐列表(包含两种推荐算法)进行优化
。能够把推荐列表看作是一个投资组合(推荐列表的每个item相当于投资组合里面的股
票 , 某个item在列表中的位置能够觉得是投资组合中某个股票的权重)
二 推荐风险分析
1、基本定义
1)、投资组合: 投资组合是一个包括n个具有相应权重的item的集合 , 权重与item的
重要性相关。
2)、用户对投资组合 的偏好程度 , 某个用户对投资组合中item i的喜好程度由ru,i
表示
User 对投资组合的偏好程度的期望与方差
3)、对于某个用户来说,当且仅当满足例如以下关系时投资组合1优于投资组合二
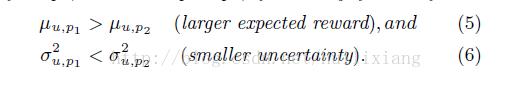
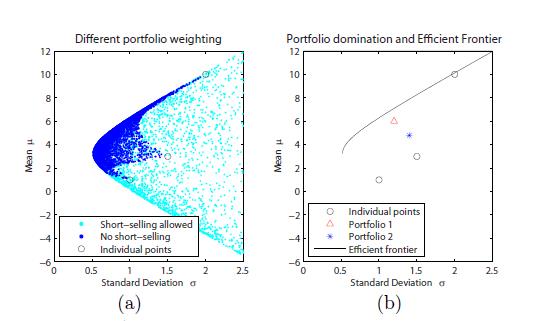
4)、 有效边界
用来描写叙述一项投资组合的风险与回报之间的关系,在以风险为横轴。预期回报率
为纵轴的坐标上显示为一条曲线。全部落在这条曲线上的风险回报组合都是在一
定风险或最低风险下能够获得的最大回报 , 如图
最佳投资组合的查找 , 假设在给定投资组合的预期回报(mean)的情况下 。
那么就是在有效边界上找风险最 小的 点。
2 、两个投资组合的风险对照
拿经典的Bayesian personalized ranking (BPR)算法和popularity-based
recommendation (POP)对照分析
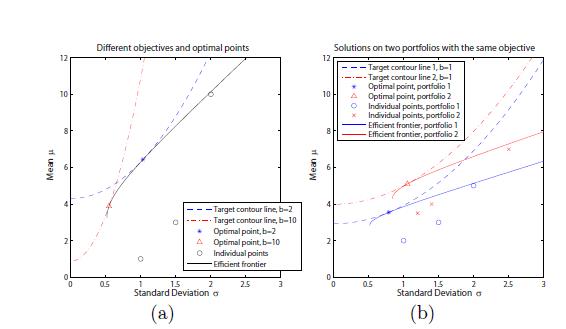
1)、用4 个典型的风险-回报 图 阐明个性化推荐与非个性化推荐之间
的关系
2)、须要三个层面来分析孰优孰劣
(1) 、物品层面:
须要计算出用户u与投资组合P中item i偏好程度的期望与方差;基于隐语
言模型的贝叶斯线性回归。
(2)、投资组合层面:
基于上一步的期望与方差。计算物品在投资组合中的权重(即排名)
(3)、两个投资组合比較层面;
採用mean-variance-aware switch algorithms进行终于的推荐选择
三 投资组合切换决策算法
1、单个item层面的评估,须要关注用户对item的偏好程序的期望和标准差。对于用
户对item评分的概率分布,在此使用probabilistic matrix factorization来建模,
先验分布 例如以下
后验分布;
用户对item评分的高斯分布为:
期望和方差为:
物品的相关性能够用 knn 或 皮尔逊相关系统算出
2、投资组合优化
主要关注投资组合中物品的权重优化分析。
以下又一次定义用户的投资期望 。 b是用户的风险规避系数 。
被减数是
期望。 凑数是方差乘以系数。
那么如今的期望-风险系统数就变成了二次曲线。有效边界与二次曲线的切点就
是该点的权重
3、选择算法
期望优先:
风险优先:
等其他算法
这仅仅是初读论文。兴许会跟进对应的推导过程解析
引用论文 To personalize or not: A risk: management perspective
以上是关于从风险管理的角度来看是否须要个性化推荐的主要内容,如果未能解决你的问题,请参考以下文章