某二叉树共有13个节点，其中有4个度为1的节点，则叶子节点数为多少

Posted 2023-04-23

叶子节点数为五。

首先由明确二叉树的基本概念以及度的基本概念。

1、二叉树：在计算机科学中，二叉树是每个结点最多有两个子树的树结构。

2、度：一个节点的子树数目，如果有一个子树那么度为1，如果没有则度为零（叶子节点），如果度为2就是有两个子树。

计算常用公式

设二叉树度为1节点个数为N1，度为2节点个数为N2，度为0节点个数为N0，总结点数为S。则有：

1）、S = N1 + N2 + N0 （按结点数计算）

2）、S= N1 + 2 × N2 + 1（按边计算）

又因为此题的N1为4，S为13，求N0，带入公式易得

所以N2 = 4， N0 = 5，由此可知叶子结点数为5。

扩展资料

二叉树性质

(1) 在非空二叉树中，第i层的结点总数不超过

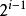
, i>=1；

(2) 深度为h的二叉树最多有

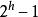
个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为

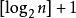
（注：[ ]表示向下取整）

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I>1，则其父结点的编号为I/2；

如果2*I<=N，则其左孩子（即左子树的根结点）的编号为2*I；若2*I>N，则无左孩子；

如果2*I+1<=N，则其右孩子的结点编号为2*I+1；若2*I+1>N，则无右孩子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。

(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i

参考资料来源：百度百科-二叉树

参考技术A

叶子节点数为5。

设度为1的节点个数为N1，度为2的节点个数为N2，度为0的节点个数为N0，总结点数为T。则有：

T = N1 + N2 + N0 （按结点数计算）------（1）

T = N1 + 2 × N2 + 1（按边计算） ----------（2）

T = 13 ---------------------------------------（3）

N1 = 4 --------------------------------------（4）

（3）（4）分别代入（1），（2）可知

N2 + N0 = 9

2 × N2 = 8

所以N2 = 4， N0 = 5，由此可知叶子结点数为5。

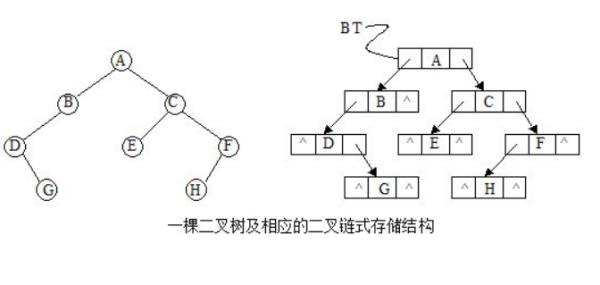
扩展资料：  

二叉树性质

(1) 在非空二叉树中，第i层的结点总数不超过

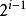
, i>=1；

(2) 深度为h的二叉树最多有

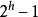
个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为

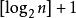
（注：[ ]表示向下取整）

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I>1，则其父结点的编号为I/2；

如果2*I<=N，则其左孩子（即左子树的根结点）的编号为2*I；若2*I>N，则无左孩子；

如果2*I+1<=N，则其右孩子的结点编号为2*I+1；若2*I+1>N，则无右孩子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。

(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i 

参考资料来源：百度百科-二叉树    

参考技术B 设度为1的节点个数为N1，度为2的节点个数为N2，度为0的节点个数为N0，总结点数为T。则有：
T = N1 + N2 + N0 （按结点数计算）------（1）
T = N1 + 2 × N2 + 1（按边计算） ----------（2）
T = 13 ---------------------------------------（3）
N1 = 4 --------------------------------------（4）
（3）（4）分别代入（1），（2）可知
N2 + N0 = 9
2 × N2 = 8
所以N2 = 4， N0 = 5，由此可知叶子结点数为5

C++程序设计创建并统计二叉树的结点个数

要求代码简单易懂！

参考技术A

头文件：binary_tree.h

#ifndef BINARYTREE
#define BINARYTREE

#include <stack>
#include <iostream> //cin>> cout<<
#include <queue>
#include <utility>
#include <iomanip> //setw()
#define MaxSize 100
#define MaxWidth 50

////用打括号的字符串来作为创建树时的输入
////例如 
//binary_tree::pbinary_tree_node T,Tnew;
//char pch[100]="A(B(F,G(H,I)),C(D(J,K),E))";
//Tnew=NULL; binary_tree::create_binary_tree(T,pch);
//binary_tree::print_binary_tree(T);
//binary_tree::copy_binary_tree(T,Tnew);
//binary_tree::print_binary_tree(Tnew);
//binary_tree::pbinary_tree_node Tnew2=binary_tree::copy_binary_tree(Tnew);
//binary_tree::print_binary_tree(Tnew2);
//binary_tree::pre_order(T);
//binary_tree::in_order(T);
//binary_tree::post_order(T);
//cout<<"leafs:";
//binary_tree::print_leaf(T);
//cout<<"number of leaf:"<<binary_tree::count_leaf(T)<<endl;
//cout<<endl;

using namespace std;
namespace binary_tree


typedef struct tnode

tnode():data('\\0'),lchild(NULL),rchild(NULL)
char data;
struct tnode *lchild,*rchild;
binary_tree_node ,*pbinary_tree_node;


void create_binary_tree(pbinary_tree_node &bt,char *str)


pbinary_tree_node St[MaxSize],p;
int top=-1,k,j=0;
char ch;
bt=NULL;
while((ch=str[j++])!='\\0')

switch(ch)

case '(':top++;St[top]=p;k=1;break;
case ')':top--;break;
case ',':k=2;break;
default:
p=new binary_tree_node;
p->data=ch;
p->lchild=p->rchild=NULL;
if(bt==NULL)
bt=p;
else

switch(k)

case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;






void create_binary_search_tree(pbinary_tree_node &bt,const vector<char>& vc)

for (vector<char>::const_iterator i=vc.begin();i!=vc.end();i++)




void print_binary_tree(pbinary_tree_node bt)
//用左右孩子的方式输出一颗树
stack<pair<pbinary_tree_node,int>> Stack;
if (bt)

Stack.push(make_pair(bt,0));

pair<pbinary_tree_node,int> onenode;
while (!Stack.empty())

onenode=Stack.top();
Stack.pop();

if (onenode.second==0)

cout<<onenode.first->data<<endl;

else if (onenode.second==1)

cout<<" --"<<onenode.first->data<<endl;

else

int depth=onenode.second;
while(--depth)

cout<<"   ";

cout<<" --"<<onenode.first->data<<endl;


if (onenode.first->lchild!=0)

Stack.push(make_pair(onenode.first->rchild,onenode.second+1));

if (onenode.first->lchild!=0)

Stack.push(make_pair(onenode.first->lchild,onenode.second+1));


cout<<endl;


void pre_order(pbinary_tree_node T)
//先序遍历输出一颗树的全部结点值1,2,3
stack<pbinary_tree_node> Stack;
if (T)

Stack.push(T);
pbinary_tree_node t;
while (!Stack.empty())

t=Stack.top();
Stack.pop();
cout<<t->data<<" ";
if (t->rchild!=0)

Stack.push(t->rchild);

if (t->lchild!=0)

Stack.push(t->lchild);


cout<<endl;




void in_order(pbinary_tree_node t)
//中序序遍历输出一颗树的全部结点值2,1,3
//广度优先遍历
stack<pbinary_tree_node> tempstack;
if (t!=NULL)

do 

tempstack.push(t);
t=t->lchild;
 while (t!=NULL);

while (!tempstack.empty())

pbinary_tree_node p=tempstack.top();
cout<<p->data<<" ";
tempstack.pop();
if (p->rchild!=NULL)

p=p->rchild;
do 

tempstack.push(p);
p=p->lchild;
 while (p!=NULL);


cout<<endl;


void post_order(pbinary_tree_node T)
//后续序序遍历输出一颗树的全部结点值2,3,1
//广度优先遍历
typedef pair<pbinary_tree_node,bool> multinode; 
stack<multinode> tempstack;
if (T)

tempstack.push(make_pair(T,false));

while (!tempstack.empty())

multinode m=tempstack.top();tempstack.pop();
if (m.first->lchild==NULL && m.first->rchild==NULL)
//叶子节点直接输出
cout<<m.first->data<<" ";

else if (m.second==true)
//所有孩子都遍历完了才会到这一步
cout<<m.first->data<<" ";

else 
//非终结点，并且孩子还没遍历完。
m.second=true;tempstack.push(m);
if (m.first->rchild!=NULL)

tempstack.push(make_pair(m.first->rchild,false));

if (m.first->lchild!=NULL)

tempstack.push(make_pair(m.first->lchild,false));



cout<<endl;

int binary_tree_hight(pbinary_tree_node bt)
//递归实现计算深度最大的路径长度
int lchilddep,rchilddep;
if(bt==NULL)
return 0;
else

lchilddep=binary_tree_hight(bt->lchild);
rchilddep=binary_tree_hight(bt->rchild);
return (lchilddep>rchilddep)?(lchilddep+1):(rchilddep+1);



int count_node(pbinary_tree_node bt)
//计算一颗树全部的结点个数
int num1,num2;
if(bt==NULL)
return 0;
else

num1=count_node(bt->lchild);
num2=count_node(bt->rchild);
return (num1+num2+1);



int count_leaf(pbinary_tree_node bt)
//返回一颗树上全部的叶节点个数
int num1,num2;
if(bt==NULL)
return 0;
else if(bt->lchild==NULL && bt->rchild==NULL)
return 1;
else

num1=count_leaf(bt->lchild);
num2=count_leaf(bt->rchild);
return (num1+num2);


void print_leaf(pbinary_tree_node bt)


if (bt==NULL)

return ;

//root first 
else if (bt->lchild==NULL && bt->rchild==NULL)

cout<<" "<<bt->data<<" ";
 
else

print_leaf(bt->lchild);
print_leaf(bt->rchild);




void level_order(pbinary_tree_node T)
//广度优先遍历一棵树的所有节点,借助一个队列，简单实现。
queue<pbinary_tree_node> Queue;
if (T)

Queue.push(T);
while (!Queue.empty())

pbinary_tree_node t=Queue.front();
Queue.pop();
cout<<t->data<<" ";
if (t->lchild!=0)

Queue.push(t->lchild);

if (t->rchild!=0)

Queue.push(t->rchild);


cout<<endl;



pbinary_tree_node find_node(pbinary_tree_node bt,char x)
//查找一颗树中是否有值为x的结点
pbinary_tree_node p;
if(bt==NULL)
return NULL;
else if(bt->data==x)
return bt;
 else
 
 p=find_node(bt->lchild,x);
 if(p!=NULL)
 return p;
 else
 return find_node(bt->rchild,x);
 


void max_node(pbinary_tree_node bt,pbinary_tree_node &p)

if(bt!=NULL)

if(bt->data>p->data)
p=bt;
max_node(bt->lchild,p);
max_node(bt->rchild,p);



void copy_binary_tree(pbinary_tree_node bt,pbinary_tree_node &newbt)

if(bt!=NULL)

newbt=(pbinary_tree_node )malloc(sizeof(binary_tree_node));
newbt->data=bt->data;
copy_binary_tree(bt->lchild,newbt->lchild);
copy_binary_tree(bt->rchild,newbt->rchild);

else
newbt=NULL;

//pbinary_tree_node copy_binary_tree(pbinary_tree_node root) 
//
// pbinary_tree_node new_root;
// if(root!=NULL)
// new_root=(pbinary_tree_node )malloc(sizeof(binary_tree_node));
// new_root->data=root->data;
// new_root->lchild=copy_binary_tree(root->lchild);
// new_root->rchild=copy_binary_tree(root->rchild);
//  
// else 
// return NULL;
// return new_root;
//
pbinary_tree_node copy_binary_tree(pbinary_tree_node bt)
//先序遍历输出一颗树的全部结点值1,2,3
stack<pbinary_tree_node> stack_left,stack_right;
pbinary_tree_node newbt;
if (bt!=NULL)

//new root
newbt=new binary_tree_node;
newbt->data=bt->data;

//travel bt and travel newbt at the same time
stack_left.push(bt);
stack_right.push(newbt);

while (!stack_left.empty())

pbinary_tree_node pleft=stack_left.top();
pbinary_tree_node pright=stack_right.top();
stack_left.pop();
stack_right.pop();
if (pleft->rchild!=0)

stack_left.push(pleft->rchild);
pright->rchild=new binary_tree_node;
pright->rchild->data=pleft->rchild->data;
stack_right.push(pright->rchild);

if (pleft->lchild!=0)

stack_left.push(pleft->lchild);
pright->lchild=new binary_tree_node;
pright->lchild->data=pleft->lchild->data;
stack_right.push(pright->lchild);



return newbt;


void delete_binary_tree(pbinary_tree_node &bt)

if(bt!=NULL)

delete_binary_tree(bt->lchild);
delete_binary_tree(bt->rchild);
delete(bt);bt=NULL;



int  size(pbinary_tree_node T)
//树的元素个数
if(T==NULL) return 0;
else return size(T->lchild)+size(T->rchild)+1;



int level(pbinary_tree_node T,pbinary_tree_node p)
//返回p所指结点的高度（高度自下往上计算）
if(T==NULL) return 0;
if(T->data==p->data ) return 1;
int h1=level(T->lchild,p );
if(h1>0) return h1+1;
int h2=level(T->rchild,p );
if(h2>0) return h2+1;
return 1;


int reflect(pbinary_tree_node T)
//交换数的左右子树
if(T==NULL) return 0;
reflect(T->lchild );
reflect(T->rchild );
pbinary_tree_node p;
p=T->rchild ;
T->rchild=T->lchild;
T->lchild=p;
return 1;

int reflect1(pbinary_tree_node T)

queue<pbinary_tree_node> queue1;
if (T!=NULL)

queue1.push(T);
while (!queue1.empty())

pbinary_tree_node temp=queue1.front();
queue1.pop();
swap(temp->lchild,temp->rchild);
if (temp->lchild!=NULL)

queue1.push(temp->lchild);

if (temp->rchild!=NULL)

queue1.push(temp->rchild);


return 1;

else

return 0;



int max_path(pbinary_tree_node &T)
//输出一条最长的根路径
if(T==NULL) return 0;
if((T->lchild==NULL)&&(T->rchild==NULL))
delete T;
T=NULL;
return 1;

else 
max_path(T->lchild );
max_path(T->rchild );
return 1;



void level_number(pbinary_tree_node T,int a[],int level)
//计算树每层的结点数
if(T!=NULL)
a[level]+=1;
level_number(T->lchild,a,level+1);
level_number(T->rchild,a,level+1);



int width(pbinary_tree_node T)
//求树的宽度
int wid,i=0;
int a[11];//树的最大层次11
for(i=0;i<11;i++) a[i]=0;
level_number(T,a,0);
for(i=0;i<11;i++) cout<<setw(3)<<a[i];
cout<<endl;
wid=a[0];
for(i=1;i<11;i++) 
if(wid<a[i]) wid=a[i];
return wid;


int height(pbinary_tree_node t)

if(t==NULL) return 0;
int hl=height(t->lchild );
int hr=height(t->rchild );
if(hl>hr) return 1+hl;
else return 1+hr;




#endif

源文件main.cpp

#include <iostream>
using namespace std;
#include "binary_tree.h"

int main()

//用打括号的字符串来作为创建树时的输入
//例如 
binary_tree::pbinary_tree_node T,Tnew;
char pch[100]="A(B(F,G(H,I)),C(D(J,K),E))";
Tnew=NULL; binary_tree::create_binary_tree(T,pch);
binary_tree::print_binary_tree(T);
binary_tree::copy_binary_tree(T,Tnew);
binary_tree::print_binary_tree(Tnew);
binary_tree::pbinary_tree_node Tnew2=binary_tree::copy_binary_tree(Tnew);
binary_tree::print_binary_tree(Tnew2);
binary_tree::pre_order(T);
binary_tree::in_order(T);
binary_tree::post_order(T);
cout<<"leafs:";
binary_tree::print_leaf(T);
cout<<"number of leaf:"<<binary_tree::count_leaf(T)<<endl;
cout<<endl;

输出：

A

 --B

    --F

    --G

       --H

       --I

 --C

    --D

       --J

       --K

    --E

A

 --B

    --F

    --G

       --H

       --I

 --C

    --D

       --J

       --K

    --E

A

 --B

    --F

    --G

       --H

       --I

 --C

    --D

       --J

       --K

    --E

A B F G H I C D J K E

F B H G I A J D K C E

F H I G B J K D E C A

leafs: F  H  I  J  K  E number of leaf:6

请按任意键继续. . .

追问

没有简短一些的吗……这也太复杂了

追答

简短的你就直接看看那个count_leaf函数的实现不就行了啊，又没让你全部看，之所以给你那么多是因为你总要输出出来能跑起来吧，