Mahout实现的分类算法，两个例子，预测期望的目标变量

Posted 2020-09-14

Mahout实现的分类算法有：

–随机梯度下降（SGD）

–贝叶斯分类(Bayes)

–在线学习算法(Online Passive Aggressive)

–隐马尔科夫模型(HMM)

–决策森林(随机森林,DF)

例子1：将位置用作预测变量

用一个使用合成数据的简单例子，演示如何选择预测变量，使Mahout的模型能够准确地预测期望的目标变量。

上图是一个历史数据集合。假设在搜索颜色填充的形状：颜色填充是目标变量。

特征可以视为包含形状，和位置的预测变量。

–位置貌似适合用作预测变量：水平(x)坐标可能就足够了。

–形状似乎并不重要

很明显，颜色填充有两种可能取值，即填充或未填充。

–现在需要选择用作预测变量的特征。哪些特征是可以正确表述的呢？

–首先排除颜色填充(它是目标变量)，可以将位置或形状用作变量。

–可以用x和y坐标来描述位置。基于一个数据表，可以为每个样本创建一条记录，包含目标变量和正在考虑的预测变量的字段。

例子2：不同数据需要不同预测变量

看看另一组历史数据，它们与之前的数据有着同样的特征。

–但在这种情况下，无论x还是y坐标，对预测符号是否填充颜色，没有作用。

–位置不再有用，但现在形状成为了一个有用的特征。

选作预测变量的特征(形状)具有3种值(圆形、三角形、正方形)。可引入朝向，来区分这些形状(朝上的三角形和朝下的三角形)

不同的算法各有优势

以前面的例子为证：

–在例1中，训练算法应该使用x坐标位置来判定颜色填充。在例2中，形状更有用。

一个点的x坐标点位置是连续变量，需要算法可以使用连续变量。

–在Mahout中，SGD和随机森林法，可以使用连续变量。

–朴素贝叶斯和补充朴素贝叶斯算法，则无法使用连续变量。

并行串行算法的权衡

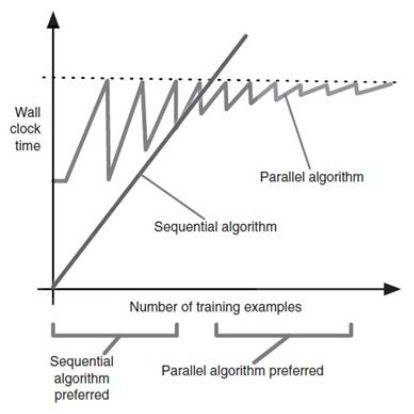
并行算法有相当大的额外开销，开始处理样本之前，需要花一些时间去设置计算环境。

对于某些中等规模的数据集，串行算法可能不仅仅是够用，而往往是首选的

这种权衡如图所示，其中比较了假设的串行，和并行可扩展算法的运行时间

锯齿形状的下降部分，是由于添加了新机器

本文出自 “中科院计算所培训” 博客，谢绝转载！