树状数组
Posted 唐世光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树状数组相关的知识,希望对你有一定的参考价值。
树状数组
基本概念
假设数组a[1..n],那么查询a[1]+...+a[n]的时间是log级别的,而且是一个在线的数据结构,支持随时修改某个元素的值,复杂度也为log级别。
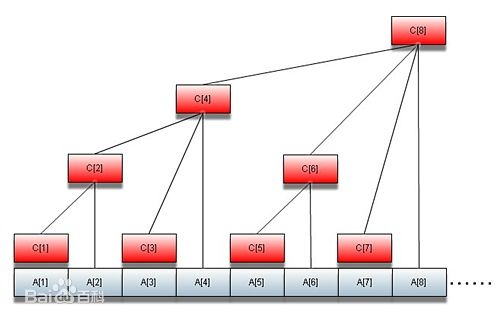
树状数组的结构图
令这棵树的结点编号为C1,C2...Cn。令每个结点的值为这棵树的值的总和,那么容易发现:
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这里有一个有趣的性质:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax,
所以很明显:Cn = A(n – 2^k + 1) + ... + An
算这个2^k有一个快捷的办法,定义一个函数如下即可:
|
1
2
3
|
int lowbit(int x){return x&(x^(x–1));} |
利用机器补码特性,也可以写成:
|
1
2
3
|
int lowbit(int x){return x&(-x);} |
当想要查询一个SUM(n)(求a[n]的和),可以依据如下算法即可:
step1: 令sum = 0,转第二步;
step2: 假如n <= 0,算法结束,返回sum值,否则sum = sum + Cn,转第三步;
step3: 令n = n – lowbit(n),转第二步。
可以看出,这个算法就是将这一个个区间的和全部加起来,为什么是效率是log(n)的呢?以下给出证明:
n = n – lowbit(n)这一步实际上等价于将n的二进制的最后一个1减去。而n的二进制里最多有log(n)个1,所以查询效率是log(n)的。
那么修改呢,修改一个节点,必须修改其所有祖先,最坏情况下为修改第一个元素,最多有log(n)的祖先。
所以修改算法如下(给某个结点i加上x):
step1: 当i > n时,算法结束,否则转第二步;
step2: Ci = Ci + x, i = i + lowbit(i)转第一步。
i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程。
对于数组求和来说树状数组简直太快了!
注:
求lowbit(x)的建议公式:
lowbit(x):=x and (x xor (x - 1));
或lowbit(x):=x and (-x);
lowbit(x)即为2^k的值。
实例代码
/******************************************
树状数组:
*****************************************/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int a[17],c[17];
//Cn = A(n – 2^k + 1) + ... + An
//算这个2^k有一个快捷的办法,定义一个函数如下即可:
int lowbit(int x)
{
return x&(-x);
}
int sum(int n)
{
int sum=0;
while(n>0)
{
sum += c[n];
n = n-lowbit(n);
}
return sum;
}
//某个几点加上一个数
void Add(int pos,int b,int max)
{
while(pos<=max)
{
c[pos] += b;
pos = pos+lowbit(pos);
}
}
//某个节点乘上一个数
void Muil(int pos,int b,int max)
{
while(pos<=max)
{
c[pos] *=b;
pos = pos + lowbit(pos);
}
}
//显示数组
void display(int* a)
{
int i;
for(i=1;i<=a[0];i++)
{
printf("%d ",a[i]);
}
printf("\\n");
}
int main()
{
int choice,num,pos,max=16;
memset(c,0,sizeof(c));
memset(a,0,sizeof(a));
c[0]=16;
a[0]=16;
printf("加(1),位置(pos)、数(a)\\n");
printf("减(-1),位置(pos)、数(a)\\n");
printf("乘(0),位置(pos)、数(a)\\n");
printf("和(2),位置(pos)、0\\n");
printf("3 0 0,显示a、c素组\\n");
while(scanf("%d%d%d",&choice,&pos,&num)!=EOF)
{
switch(choice)
{
case 1:
a[pos] +=num;
Add(pos,num,max);
break;
case -1:
a[pos] -=num;
Add(pos,(-1)*num,max);
break;
case 0:
a[pos] *=num;
Muil(pos,num,max);
break;
case 2:
printf("%d\\n",sum(pos));
break;
case 3:
display(a);
display(c);
}
}
return 0;
}
以上是关于树状数组的主要内容,如果未能解决你的问题,请参考以下文章
